Saturday Quiz – November 27, 2010 – answers and discussion

Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

According to the theory of the money multiplier that changes in the monetary base are driven by changes in the money supply.

The answer is False.

Mainstream macroeconomics textbooks are completely wrong when they discuss the credit-creation capacity of commercial banks. The concept of the money multiplier is at the centre of this analysis and posits that the multiplier m transmits changes in the so-called monetary base (MB) (the sum of bank reserves and currency at issue) into changes in the money supply (M). The chapters on money usually present some arcane algebra which is deliberately designed to impart a sense of gravitas or authority to the students who then mindlessly ape what is in the textbook.

They rehearse the argument in their undergraduate courses (introductory and intermediate macroeconomics; money and banking; monetary economics etc) that the money multiplier is usually expressed as the inverse of the required reserve ratio plus some other novelties relating to preferences for cash versus deposits by the public.

Accordingly, the students learn that if the central bank told private banks that they had to keep 10 per cent of total deposits as reserves then the required reserve ratio (RRR) would be 0.10 and m would equal 1/0.10 = 10. More complicated formulae are derived when you consider that people also will want to hold some of their deposits as cash. But these complications do not add anything to the story.

The formula for the determination of the money supply is: M = m x MB. So if a $1 is newly deposited in a bank, the money supply will rise (be multiplied) by $10 (if the RRR = 0.10). The way this multiplier is alleged to work is explained as follows (assuming the bank is required to hold 10 per cent of all deposits as reserves):

• A person deposits say $100 in a bank.
• To make money, the bank then loans the remaining $90 to a customer.
• They spend the money and the recipient of the funds deposits it with their bank.
• That bank then lends 0.9 times $90 = $81 (keeping 0.10 in reserve as required).
• And so on until the loans become so small that they dissolve to zero

None of this is remotely accurate in terms of depicting how the banks make loans. It is an important device for the mainstream because it implies that banks take deposits to get funds which they can then on-lend. But prudential regulations require they keep a little in reserve. So we get this credit creation process ballooning out due to the fractional reserve requirements.

The money multiplier myth also leads students to think that as the central bank can control the monetary base then it can control the money supply. Further, given that inflation is allegedly the result of the money supply growing too fast then the blame is sheeted home to the “government”. This leads to claims that if the government runs a budget deficit then it has to issue bonds to avoid causing hyperinflation. Nothing could be further from the truth.

That is nothing like the way the banking system operates in the real world. The idea that the monetary base (the sum of bank reserves and currency) leads to a change in the money supply via some multiple is not a valid representation of the way the monetary system operates.

First, the central bank does not have the capacity to control the money supply in a modern monetary system. In the world we live in, bank loans create deposits and are made without reference to the reserve positions of the banks. The bank then ensures its reserve positions are legally compliant as a separate process knowing that it can always get the reserves from the central bank. The only way that the central bank can influence credit creation in this setting is via the price of the reserves it provides on demand to the commercial banks.

Second, this suggests that the decisions by banks to lend may be influenced by the price of reserves rather than whether they have sufficient reserves. They can always get the reserves that are required at any point in time at a price, which may be prohibitive.

Third, the money multiplier story has the central bank manipulating the money supply via open market operations. So they would argue that the central bank might buy bonds to the public to increase the money base and then allow the fractional reserve system to expand the money supply. But a moment’s thought will lead you to conclude this would be futile unless (as in Question 3 a support rate on excess reserves equal to the current policy rate was being paid).

Why? The open market purchase would increase bank reserves and the commercial banks, in lieu of any market return on the overnight funds, would try to place them in the interbank market. Of-course, any transactions at this level (they are horizontal) net to zero so all that happens is that the excess reserve position of the system is shuffled between banks. But in the process the interbank return would start to fall and if the process was left to resolve, the overnight rate would fall to zero and the central bank would lose control of its monetary policy position (unless it was targetting a zero interest rate).

In lieu of a support rate equal to the target rate, the central bank would have to sell bonds to drain the excess reserves. The same futility would occur if the central bank attempted to reduce the money supply by instigating an open market sale of bonds.

In all cases, the central bank cannot influence the money supply in this way.

Fourth, given that the central bank adds reserves on demand to maintain financial stability and this process is driven by changes in the money supply as banks make loans which create deposits.

So the operational reality is that the dynamics of the monetary base (MB) are driven by the changes in the money supply which is exactly the reverse of the causality presented by the monetary multiplier.

So in fact we might write MB = M/m.

You might like to read these blogs for further information:

• Teaching macroeconomics students the facts
• Lost in a macroeconomics textbook again
• Lending is capital- not reserve-constrained
• Oh no … Bernanke is loose and those greenbacks are everywhere
• Building bank reserves will not expand credit
• Building bank reserves is not inflationary
• 100-percent reserve banking and state banks
• Money multiplier and other myths

Question 2:

If the nation is running a current account deficit which is accompanied by a government sector surplus of equal proportion to GDP, then the private domestic sector is spending more than they are earning and increasing its indebtedness.

The answer is True.

This is a question about the sectoral balances – the government budget balance, the external balance and the private domestic balance – that have to always add to zero because they are derived as an accounting identity from the national accounts.

To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

From the uses perspective, national income (GDP) can be used for:

GDP = C + S + T

which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.

Equating these two perspectives we get:

C + S + T = GDP = C + I + G + (X – M)

So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.

(I – S) + (G – T) + (X – M) = 0

That is the three balances have to sum to zero. The sectoral balances derived are:

• The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
• The Budget Deficit (G – T) – negative if in surplus, positive if in deficit.
• The Current Account balance (X – M) – positive if in surplus, negative if in deficit.

These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.

A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).

This is also a basic rule derived from the national accounts and has to apply at all times.

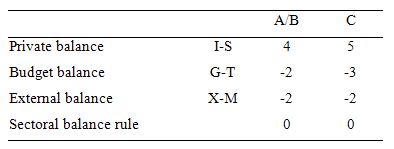
The following Table represents three options in percent of GDP terms. To aid interpretation remember that (I-S) > 0 means that the private domestic sector is spending more than they are earning; that (G-T) < 0 means that the government is running a surplus because T > G; and (X-M) < 0 means the external position is in deficit because imports are greater than exports.

The first two possibilities we might call A and B:

A: A nation can run a current account deficit with an offsetting government sector surplus, while the private domestic sector is spending less than they are earn
B: A nation can run a current account deficit with an offsetting government sector surplus, while the private domestic sector is spending more than they are earning.

So Option A says the private domestic sector is saving overall, whereas Option B say the private domestic sector is dis-saving (and going into increasing indebtedness). These options are captured in the first column of the Table. So the arithmetic example depicts an external sector deficit of 2 per cent of GDP and an offsetting budget surplus of 2 per cent of GDP.

You can see that the private sector balance is positive (that is, the sector is spending more than they are earning – Investment is greater than Saving – and has to be equal to 4 per cent of GDP.

Given that the only proposition that can be true is:

B: A nation can run a current account deficit with an offsetting government sector surplus, while the private domestic sector is spending more than they are earning.

Column 2 in the Table captures Option C:

C: A nation can run a current account deficit with a government sector surplus that is larger, while the private domestic sector is spending less than they are earning.

So the current account deficit is equal to 2 per cent of GDP while the surplus is now larger at 3 per cent of GDP. You can see that the private domestic deficit rises to 5 per cent of GDP to satisfy the accounting rule that the balances sum to zero.

The Table data also shows the rule that the sectoral balances add to zero because they are an accounting identity is satisfied in both cases.

So what is the economic rationale for this result?

If the nation is running an external deficit it means that the contribution to aggregate demand from the external sector is negative – that is net drain of spending – dragging output down.

The external deficit also means that foreigners are increasing financial claims denominated in the local currency. Given that exports represent a real costs and imports a real benefit, the motivation for a nation running a net exports surplus (the exporting nation in this case) must be to accumulate financial claims (assets) denominated in the currency of the nation running the external deficit.

A fiscal surplus also means the government is spending less than it is “earning” and that puts a drag on aggregate demand and constrains the ability of the economy to grow.

In these circumstances, for income to be stable, the private domestic sector has to spend more than they earn.

You can see this by going back to the aggregate demand relations above. For those who like simple algebra we can manipulate the aggregate demand model to see this more clearly.

Y = GDP = C + I + G + (X – M)

which says that the total national income (Y or GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

So if the G is spending less than it is “earning” and the external sector is adding less income (X) than it is absorbing spending (M), then the other spending components must be greater than total income

The following blogs may be of further interest to you:

• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!

Question 3:

With the Eurozone nations unable to gain competitive relief via nominal exchange rate adjustments the hope is that by deflating wages and prices real unit labour costs will fall. Assuming other nations do nothing and wages and prices fall at the same rate, then a real exchange rate depreciation (relative to other nations) requires labour productivity and employment growth to rise.

The answer is False.

The EMU countries cannot improve their international competitiveness by exchange rate depreciation, which is the option always available to a fully sovereign nation issuing its own currency and floating it in foreign exchange markets.

Thus, to improve their international competitiveness, the EMU countries have to engage in “internal devaluation” which means they have to cut real unit labour costs – which are the real cost of producing goods and services. Governments setting out on this policy path have to engineer cuts in the wage and price levels (the latter following the former as unit costs fall).

But the question demonstrates that it takes more than just a nominal deflation. The strategy hinges on whether you can also engineer productivity growth (typically).

Given the assumption (wage and prices falling at the same rate), what happens to employment growth is irrelevant.

Some explanatory notes to accompany the analysis that follows:

• Employment is measured in persons (averaged over the period).
• Labour productivity is the units of output per person employment per period.
• The wage and price level are in nominal units; the real wage is the wage level divided by the price level and tells us the real purchasing power of that nominal wage level.
• The wage bill is employment times the wage level and is the total labour costs in production for each period.
• Real GDP is thus employment times labour productivity and represents a flow of actual output per period; Nominal GDP is Real GDP at market value – that is, multiplied by the price level. So real GDP can grow while nominal GDP can fall if the price level is deflating and productivity growth and/or employment growth is positive.
• The wage share is the share of total wages in nominal GDP and is thus a guide to the distribution of national income between wages and profits.
• Unit labour costs are in nominal terms and are calculated as total labour costs divided by nominal GDP. So they tell you what each unit of output is costing in labour outlays; Real unit labour costs just divide this by the price level to give a real measure of what each unit of output is costing. RULC is also the ratio of the real wage to labour productivity and through algebra I would be able to show you (trust me) that it is equivalent to the Wage share measure (although I have expressed the latter in percentage terms and left the RULC measure in raw units).

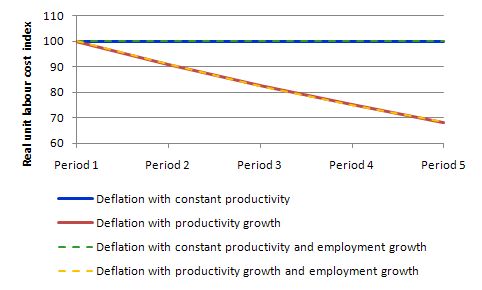
The following table models the constant and growing productivity cases but holds employment constant for five periods. We assume that the nominal wage and the price level deflate by 10 per cent per period over Period 2 to 5. In the productivity growth case, we assume it grows by 10 per cent per period over Period 2 to 5.

It is quite clear that under the assumptions employed, RULC cannot fall without productivity growth. The only other way to accomplish this is to ensure that nominal wages fall faster than the price level falls. In the historical debate, this was a major contention between Keynes and Pigou (an economist in the neo-classical tradition who best represented the so-called “British Treasury View” in the 1930s. The Treasury View thought the cure to the Great Depression was to cut the real wage because according to their erroneous logic, unemployment could only occur if the real wage was too high.

Keynes argued that if you tried to cut nominal wages as a way of cutting the real wage (given there is no such thing as a real wage that policy can directly manipulate), firms will be forced by competition to cut prices to because unit labour costs would be lower. He hypothesised that there is no reason not to believe that the rate of deflation in nominal wage and price level would be similar and so the real wage would be constant over the period of the deflation. So that is the operating assumption here.

The following table models the constant and growing productivity cases as above but allows employment to grow by 10 per cent per period. All four scenarios in the Table are them modelled in the following graph with the Real Unit Labour Costs converted into index number form equal to 100 in Period 1. As you can see what happens to employment makes no difference at all.

I could have also modelled employment falling with the same results.

The following graph shows the four scenarios shown in the last two tables. I have dashed some scenarios to make the lines visible (given that Case A and Case C) are equivalent as are Case B and Case D. What you learn is that if wages and prices fall at the same rate and labour productivity does not rise there can be no reduction in unit or real unit labour costs.

So the internal devaluation strategy relies heavily on productivity growth occurring. The literature on organisational psychology and industrial relations is replete of examples where worker morale is an important ingredient in accomplishing productivity growth. In a climate of austerity characteristic of an internal devaluation strategy it is highly likely that productivity will not grow and may even fall over time. Then the internal devaluation strategy is useless.

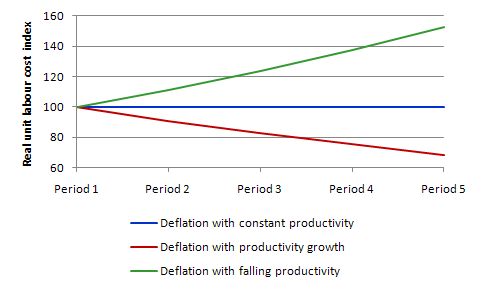
This graph compares the two scenarios in the first Table with the more realistic one that labour productivity actually falls as the government ravages the economy in pursuit of its internal devaluation. As you can see real unit labour costs rise as labour productivity falls and the economy’s competitiveness (given the exchange rate is fixed) falls.

Of-course, this “supply-side” scenario does not take into account the overwhelming reality that for an economy to realise this level of output over an extended period aggregate demand would have to be supportive. The internal devaluation strategy relies heavily on the external sector providing the demand impetus.

Given that Eurozone trade is heavily internal, it seems far fetched to assume that the trade impact arising from any successful internal devaluation will be sufficient to overcome the devastating domestic contraction in demand that will almost certainly occur. This is why commentators are calling for a domestic expansion in Germany to boost aggregate demand throughout the EMU, given the dominance of the German economy in the overall European trade.

That is clearly unlikely to happen given Germany has been engaged in a lengthy process of internal devaluation itself and the Government is resistant to any stimulus packages that might improve things within Germany and beyond via the trade impacts.

The following blogs may be of further interest to you:

• Euro zone’s self-imposed meltdown
• A Greek tragedy …
• España se está muriendo
• Exiting the Euro?
• Doomed from the start
• Europe – bailout or exit?
• Not the EMF … anything but the EMF!
• EMU posturing provides no durable solution
• Protect your workers for the sake of the nation
• The bullies and the bullied
• Modern monetary theory in an open economy

Question 4:

In a stock-flow consistent macroeconomics, we know that flows during a period add to relevant stocks at the end of the period. Accordingly, government and private investment spending are two examples of spending flows that add to the stock of aggregate demand which in turn impacts on Gross Domestic Product (National Income) because spending equals income.

The answer is false.

Spending definitely equals income but that is not the point of the question, which is, in fact, a very easy test of the difference between flows and stocks.

All expenditure aggregates – such as government spending and investment spending are flows. They add up to total expenditure or aggregate demand which is also a flow rather than a stock. Aggregate demand (a flow) in any period and it jointly determines the flow of income and output in the same period (that is, GDP) (in partnership with aggregate supply).

So while flows can add to stock – for example, the flow of saving adds to wealth or the flow of investment adds to the stock of capital – flows can also be added together to form a “larger” flow.

For example, if you wanted to work out annual GDP from the quarterly national accounts you would sum the individual quarterly observations for the 12-month period of interest. Conversely, employment is a stock so if you wanted to create an annual employment time series you would average the individual quarterly observations for the 12-month period of interest.

The following blog may be of further interest to you:

• Stock-flow consistent macro models

Premium Question 5:

Many countries are facing higher public debt to GDP ratios as a consequence of the crisis and some are approaching 100 per cent. Assume the current public debt to GDP ratio is 100 per cent and that central banks keep nominal interest rates and inflation constant and zero. While fiscal austerity is likely to prolong the recession, it is still possible to reduce the public debt to GDP ratio (under these circumstances), if the primary budget surplus to GDP ratio is higher than the negative GDP growth rate that results.

The answer is True.

First, some background.

While Modern Monetary Theory (MMT) places no particular importance in the public debt to GDP ratio for a sovereign government, given that insolvency is not an issue, the mainstream debate is dominated by the concept.

The unnecessary practice of fiat currency-issuing governments of issuing public debt $-for-$ to match public net spending (deficits) ensures that the debt levels will rise when there are deficits.

Rising deficits usually mean declining economic activity (especially if there is no evidence of accelerating inflation) which suggests that the debt/GDP ratio may be rising because the denominator is also likely to be falling or rising below trend.

Further, historical experience tells us that when economic growth resumes after a major recession, during which the public debt ratio can rise sharply, the latter always declines again.

It is this endogenous nature of the ratio that suggests it is far more important to focus on the underlying economic problems which the public debt ratio just mirrors.

Mainstream economics starts with the flawed analogy between the household and the sovereign government such that any excess in government spending over taxation receipts has to be “financed” in two ways: (a) by borrowing from the public; and/or (b) by “printing money”.

Neither characterisation is remotely representative of what happens in the real world in terms of the operations that define transactions between the government and non-government sector.

Further, the basic analogy is flawed at its most elemental level. The household must work out the financing before it can spend. The household cannot spend first. The government can spend first and ultimately does not have to worry about financing such expenditure.

However, in mainstream (dream) land, the framework for analysing these so-called “financing” choices is called the government budget constraint (GBC). The GBC says that the budget deficit in year t is equal to the change in government debt over year t plus the change in high powered money over year t. So in mathematical terms it is written as:

Which you can read in English as saying that Budget deficit = Government spending + Government interest payments – Tax receipts must equal (be “financed” by) a change in Bonds (B) and/or a change in high powered money (H). The triangle sign (delta) is just shorthand for the change in a variable.

However, this is merely an accounting statement. In a stock-flow consistent macroeconomics, this statement will always hold. That is, it has to be true if all the transactions between the government and non-government sector have been corrected added and subtracted.

So in terms of MMT, the previous equation is just an ex post accounting identity that has to be true by definition and has not real economic importance.

But for the mainstream economist, the equation represents an ex ante (before the fact) financial constraint that the government is bound by. The difference between these two conceptions is very significant and the second (mainstream) interpretation cannot be correct if governments issue fiat currency (unless they place voluntary constraints on themselves to act as if it is).

Further, in mainstream economics, money creation is erroneously depicted as the government asking the central bank to buy treasury bonds which the central bank in return then prints money. The government then spends this money. This is called debt monetisation and you can find out why this is typically not a viable option for a central bank by reading the Deficits 101 suite – Deficit spending 101 – Part 1 – Deficit spending 101 – Part 2 – Deficit spending 101 – Part 3.

Anyway, the mainstream claims that if governments increase the money growth rate (they erroneously call this “printing money”) the extra spending will cause accelerating inflation because there will be “too much money chasing too few goods”! Of-course, we know that proposition to be generally preposterous because economies that are constrained by deficient demand (defined as demand below the full employment level) respond to nominal demand increases by expanding real output rather than prices. There is an extensive literature pointing to this result.

So when governments are expanding deficits to offset a collapse in private spending, there is plenty of spare capacity available to ensure output rather than inflation increases.

But not to be daunted by the “facts”, the mainstream claim that because inflation is inevitable if “printing money” occurs, it is unwise to use this option to “finance” net public spending.

Hence they say as a better (but still poor) solution, governments should use debt issuance to “finance” their deficits. They also claim this is a poor option because in the short-term it is alleged to increase interest rates and in the longer-term is results in higher future tax rates because the debt has to be “paid back”.

Neither proposition bears scrutiny – you can read these blogs – Will we really pay higher taxes? and Will we really pay higher interest rates? – for further discussion on these points.

The mainstream textbooks are full of elaborate models of debt pay-back, debt stabilisation etc which all claim (falsely) to “prove” that the legacy of past deficits is higher debt and to stabilise the debt, the government must eliminate the deficit which means it must then run a primary surplus equal to interest payments on the existing debt.

A primary budget balance is the difference between government spending (excluding interest rate servicing) and taxation revenue.

The standard mainstream framework, which even the so-called progressives (deficit-doves) use, focuses on the ratio of debt to GDP rather than the level of debt per se. The following equation captures the approach:

So the change in the debt ratio is the sum of two terms on the right-hand side: (a) the difference between the real interest rate (r) and the GDP growth rate (g) times the initial debt ratio; and (b) the ratio of the primary deficit (G-T) to GDP.

The real interest rate is the difference between the nominal interest rate and the inflation rate.

This standard mainstream framework is used to highlight the dangers of running deficits. But even progressives (not me) use it in a perverse way to justify deficits in a downturn balanced by surpluses in the upturn.

The question notes that “some mainstream economists” claim that a ratio of 80 per cent is a dangerous threshold that should not be passed – this is the Reinhart and Rogoff story.

Many mainstream economists and a fair number of so-called progressive economists say that governments should as some point in the business cycle run primary surpluses (taxation revenue in excess of non-interest government spending) to start reducing the debt ratio back to “safe” territory.

Almost all the media commentators that you read on this topic take it for granted that the only way to reduce the public debt ratio is to run primary surpluses. That is what the whole “credible exit strategy” hoopla is about.

Further, there is no analytical definition ever provided of what safe is and fiscal rules such as those imposed on the Eurozone nations by the Stability and Growth Pact (a maximum public debt ratio of 60 per cent) are totally arbitrary and without any foundation at all. Just numbers plucked out of the air by those who do not understand the monetary system.

MMT does not tell us that a currency-issuing government running a deficit can never reduce the debt ratio. The standard formula above can easily demonstrate that a nation running a primary deficit can reduce its public debt ratio over time as long as economic growth is strong enough.

Furthermore, depending on contributions from the external sector, a nation running a deficit will more likely create the conditions for a reduction in the public debt ratio than a nation that introduces an austerity plan aimed at running primary surpluses.

Here is why that is the case.

A growing economy can absorb more debt and keep the debt ratio constant or falling. From the formula above, if the primary budget balance is zero, public debt increases at a rate r but the public debt ratio increases at r – g.

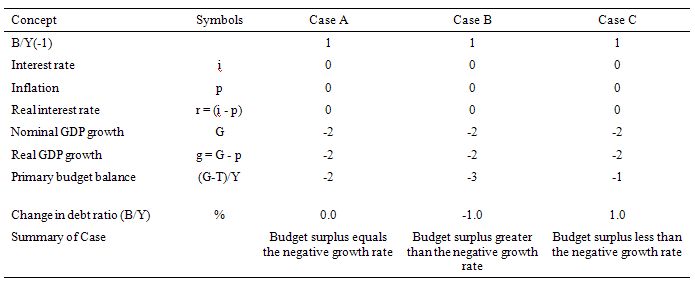
Consider this example which is captured in Year 1 in the Table below.

To make matters simple, assume a public debt ratio at the start of the period of 100 per cent (so B/Y(-1) = 1).

Assume that the rate of real GDP growth is minus 2 per cent (that is, the nation is in recession) and the automatic stabilisers push the primary budget balance into deficit equal to 1 per cent of GDP. As a consequence, the public debt ratio will rise by 3 per cent.

The government reacts to the recession in the correct manner and increases its discretionary net spending to take the deficit in Year 2 to 2 per cent of GDP (noting a positive number in this instance is a deficit).

The central bank maintains its zero interest rate policy and the inflation rate also remains at zero.

The increasing deficit stimulates economic growth in Year 2 such that real GDP grows by 2 per cent. In this case the public debt ratio falls by 0.1 per cent.

So even with an increasing (or unchanged) deficit, real GDP growth can reduce the public debt ratio, which is what has happened many times in past history following economic slowdowns.

Economists like Krugman and Mankiw argue that the government could (should) reduce the ratio by inflating it away. Noting that nominal GDP is the product of the price level (P) and real output (Y), the inflating story just increases the nominal value of output and so the denominator of the public debt ratio grows faster than the numerator.

But stimulating real growth (that is, in Y) is the other more constructive way of achieving the same relative adjustment in the denominator of the public debt ratio and its numerator.

But the best way to reduce the public debt ratio is to stop issuing debt. A sovereign government doesn’t have to issue debt if the central bank is happy to keep its target interest rate at zero or pay interest on excess reserves.

The discussion also demonstrates why tightening monetary policy makes it harder for the government to reduce the public debt ratio – which, of-course, is one of the more subtle mainstream ways to force the government to run surpluses.

Now the assumptions in the question:

• Current public debt to GDP ratio is 100 per cent = 1.
• Nominal interest rate (i) and the inflation rate (p) remain constant and zero, which means the real interest rate (r = i – p) = 0.

The following Table shows three cases:

• Case A – Budget surplus to GDP ratio equals the negative GDP growth rate.
• Case B – Budget surplus to GDP ratio greater than the negative GDP growth rate.
• Case C – Budget surplus to GDP ratio less than the negative GDP growth rate.

As a result of modelling the assumptions in the formula (above) we can see that the change in the debt ratio (B/Y) is zero in the event of Case A, falls in the event of Case B (by 1 per cent) and rises in the event of Case C (by 1 per cent).

As long as the primary surplus as a per cent of GDP is exactly equal to the negative GDP growth rate, there can be no reduction in the public debt ratio, under the circumstances (which are the most benign possible).

So it is possible under Case B where the primary budget surplus is 3 per cent (noting that the surplus is presented as a negative figure) and the contraction in real GDP is 2 percent for the debt ratio to fall.

How likely is it that this would occur in the real world when the government was pursuing such a fiscal path? Answer: unlikely.

First, fiscal austerity will probably push the GDP growth rate further into negative territory which, other things equal, pushes the public debt ratio up. Why? The budget balance is endogenous (that is, depends on private activity levels) because of the importance of the automatic stabilisers.

As GDP contracts, tax revenue falls and welfare outlays rise. It is highly likely that the government would not succeed in achieving a budget surplus under these circumstances.

So as GDP growth declines further, the automatic stabilisers will push the balance result towards (and into after a time) deficit, which, given the borrowing rules that governments volunatarily enforce on themselves, also pushed the public debt ratio up.

So austerity packages, quite apart from their highly destructive impacts on real standards of living and social standards, typically fail to reduce public debt ratios and usually increase them.

So even if you were a conservative and erroneously believed that high public debt ratios were the devil’s work, it would be foolish (counter-productive) to impose fiscal austerity on a nation as a way of addressing your paranoia. Better to grit your teeth and advocate higher deficits and higher real GDP growth.

That strategy would also be the only one advocated by MMT.

That is enough for today!