The Weekend Quiz – March 3-4, 2018 – answers and discussion

Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

After economic growth resumes, the government can rely on the automatic stabilisers to return the fiscal balance to its appropriate level.

The answer is False.

The automatic stabilisers do operate in a counter-cyclical fashion when economic growth resumes. This is because tax revenue improves given it is typically tied to income generation in some way. Further, most governments provide transfer payment relief to workers (unemployment benefits) and this increases when there is an economic slowdown.

But the government cannot rely on this process to ensure its fiscal balance is aligned with full employment and the overall spending and saving desires of the non-government sector.

The automatic stabilisers just push the fiscal balance towards deficit, into deficit, or into a larger deficit when GDP growth declines and vice versa when GDP growth increases. These movements in aggregate demand play an important counter-cyclical attenuating role. So when GDP is declining due to falling aggregate demand, the automatic stabilisers work to add demand (falling taxes and rising welfare payments). When GDP growth is rising, the automatic stabilisers start to pull demand back as the economy adjusts (rising taxes and falling welfare payments).

We also measure the automatic stabiliser impact against some benchmark or “full capacity” or potential level of output, so that we can decompose the fiscal balance into that component which is due to specific discretionary fiscal policy choices made by the government and that which arises because the cycle takes the economy away from the potential level of output.

This decomposition provides (in modern terminology) the structural (discretionary) and cyclical fiscal balances. The fiscal components are adjusted to what they would be at the potential or full capacity level of output.

So if the economy is operating below capacity then tax revenue would be below its potential level and welfare spending would be above. In other words, the fiscal balance would be smaller at potential output relative to its current value if the economy was operating below full capacity. The adjustments would work in reverse should the economy be operating above full capacity.

If the fiscal outcome is in deficit when computed at the “full employment” or potential output level, then we call this a structural deficit and it means that the overall impact of discretionary fiscal policy is expansionary irrespective of what the actual fiscal outcome is presently. If it is in surplus, then we have a structural surplus and it means that the overall impact of discretionary fiscal policy is contractionary irrespective of what the actual fiscal outcome is presently.

So you could have a downturn which drives the fiscal outcome into a deficit but the underlying structural position could be contractionary (that is, a surplus). And vice versa.

The difference between the actual fiscal outcome and the structural component is then considered to be the cyclical fiscal outcome and it arises because the economy is deviating from its potential.

In some of the blogs listed below I go into the measurement issues involved in this decomposition in more detail. However for this question it these issues are less important to discuss.

The point is that structural fiscal balance has to be sufficient to ensure there is full employment. The only sensible reason for accepting the authority of a national government and ceding currency control to such an entity is that it can work for all of us to advance public purpose.

In this context, one of the most important elements of public purpose that the state has to maximise is employment. Once the private sector has made its spending (and saving decisions) based on its expectations of the future, the government has to render those private decisions consistent with the objective of full employment.

Given the non-government sector will typically desire to net save (accumulate financial assets in the currency of issue) over the course of a business cycle this means that there will be, on average, a spending gap over the course of the same cycle that can only be filled by the national government. There is no escaping that.

So then the national government has a choice – maintain full employment by ensuring there is no spending gap which means that the necessary deficit is defined by this political goal. It will be whatever is required to close the spending gap. However, it is also possible that the political goals may be to maintain some slack in the economy (persistent unemployment and underemployment) which means that the government deficit will be somewhat smaller and perhaps even, for a time, a fiscal surplus will be possible.

But the second option would introduce fiscal drag (deflationary forces) into the economy which will ultimately cause firms to reduce production and income and drive the fiscal outcome towards increasing deficits.

Ultimately, the spending gap is closed by the automatic stabilisers because falling national income ensures that that the leakages (saving, taxation and imports) equal the injections (investment, government spending and exports) so that the sectoral balances hold (being accounting constructs). But at that point, the economy will support lower employment levels and rising unemployment. The fiscal outcome will also be in deficit – but in this situation, the deficits will be what I call “bad” deficits. Deficits driven by a declining economy and rising unemployment.

So fiscal sustainability requires that the government fills the spending gap with “good” deficits at levels of economic activity consistent with full employment – which I define as 2 per cent unemployment and zero underemployment.

Fiscal sustainability cannot be defined independently of full employment. Once the link between full employment and the conduct of fiscal policy is abandoned, we are effectively admitting that we do not want government to take responsibility of full employment (and the equity advantages that accompany that end).

So it will not always be the case that the dynamics of the automatic stabilisers will leave a structural deficit sufficient to finance the saving desire of the non-government sector at an output level consistent with full utilisation of resources.

The following blogs may be of further interest to you:

• A modern monetary theory lullaby
• Saturday Quiz – April 24, 2010 – answers and discussion
• The dreaded NAIRU is still about!
• Structural deficits – the great con job!
• Structural deficits and automatic stabilisers
• Another economics department to close

Question 2:

Only one of the following combinations is possible for a nation (balances expressed as a proportion of GDP):

• Current account deficit equal in size to government surplus, and private domestic sector saving overall.
• Current account deficit equal in size to government surplus, and private domestic sector dissaving overall.
• Current account deficit smaller in size to government surplus, and private domestic sector saving overall.
• None of the above are possible as they all defy the sectoral balances accounting identity.

The best answer is the second option – “Current account deficit equal in size to government surplus, and private domestic sector dissaving overall”.

This is a question about the sectoral balances – the government fiscal balance, the external balance and the private domestic balance – that have to always add to zero because they are derived as an accounting identity from the national accounts.

To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

(1) GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.

We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all tax revenue minus total transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).

Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).

Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):

(2) GNP = C + I + G + (X – M) + FNI

To render this approach into the sectoral balances form, we subtract total net taxes (T) from both sides of Expression (3) to get:

(3) GNP – T = C + I + G + (X – M) + FNI – T

Now we can collect the terms by arranging them according to the three sectoral balances:

(4) (GNP – C – T) – I = (G – T) + (X – M + FNI)

The the terms in Expression (4) are relatively easy to understand now.

The term (GNP – C – T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.

The left-hand side of Equation (4), (GNP – C – T) – I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP – C – T).

In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.

The term (G – T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.

Finally, the other right-hand side term (X – M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.

In English we could say that:

The private financial balance equals the sum of the government financial balance plus the current account balance.

We can re-write Expression (6) in this way to get the sectoral balances equation:

(5) (S – I) = (G – T) + CAD

which is interpreted as meaning that government sector deficits (G – T > 0) and current account surpluses (CAD > 0) generate national income and net financial assets for the private domestic sector.

Conversely, government surpluses (G – T < 0) and current account deficits (CAD < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets.

Expression (5) can also be written as:

(6) [(S – I) – CAD] = (G – T)

where the term on the left-hand side [(S – I) – CAD] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance.

This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit).

The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers.

All these relationships (equations) hold as a matter of accounting and not matters of opinion.

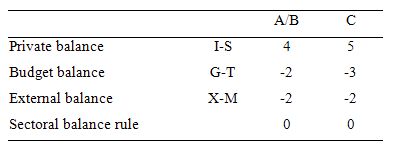
The following Table represents the three options in percent of GDP terms. To aid interpretation remember that (I-S) > 0 means that the private domestic sector is spending more than they are earning; that (G-T) < 0 means that the government is running a surplus because T > G; and (X-M) < 0 means the external position is in deficit because imports are greater than exports.

The first two possibilities we might call A and B:

A. Current account deficit equal in size to government surplus, and private domestic sector saving overall.

B. Current account deficit equal in size to government surplus, and private domestic sector dissaving overall.

So Option A says the private domestic sector is saving overall, whereas Option B say the private domestic sector is dissaving (and going into increasing indebtedness).

The first column of the Table depicts an external sector deficit of 2 per cent of GDP and an offsetting fiscal surplus of 2 per cent of GDP.

You can see that the private sector balance is positive (that is, the sector is spending more than they are earning – Investment is greater than Saving – and has to be equal to 4 per cent of GDP.

Given that the only proposition that can be true is:

B: Current account deficit equal in size to government surplus, and private domestic sector dissaving overall.

Column 2 in the Table captures Option C:

C: Current account deficit smaller in size to government surplus, and private domestic sector saving overall..

So the current account deficit is equal to 2 per cent of GDP while the surplus is now larger at 3 per cent of GDP. You can see that the private domestic deficit rises to 5 per cent of GDP to satisfy the accounting rule that the balances sum to zero.

The final option available is:

D: None of the above are possible as they all defy the sectoral balances accounting identity.

It cannot be true because as the Table data shows the rule that the sectoral balances add to zero because they are an accounting identity is satisfied in both cases.

So what is the economic rationale for this result?

If the nation is running an external deficit it means that the contribution to aggregate demand from the external sector is negative – that is net drain of spending – dragging output down.

The external deficit also means that foreigners are increasing financial claims denominated in the local currency. Given that exports represent a real costs and imports a real benefit, the motivation for a nation running a net exports surplus (the exporting nation in this case) must be to accumulate financial claims (assets) denominated in the currency of the nation running the external deficit.

A fiscal surplus also means the government is spending less than it is “earning” and that puts a drag on aggregate demand and constrains the ability of the economy to grow.

In these circumstances, for income to be stable, the private domestic sector has to spend more than they earn.

You can see this by going back to the aggregate demand relations above. For those who like simple algebra we can manipulate the aggregate demand model to see this more clearly.

Y = GDP = C + I + G + (X – M)

which says that the total national income (Y or GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

So if the G is spending less than it is “earning” and the external sector is adding less income (X) than it is absorbing spending (M), then the other spending components must be greater than total income

The following blogs may be of further interest to you:

• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!

Question 3:

The Eurozone nations have to endure internal devaluation (nominal wages and prices deflation and/or productivity growth) to adjust to external imbalances. It is claimed that this process will the individual nations more competitive as long as real unit labour costs fall faster than their trading partners. However, ignoring whether the logic is correct or not, which of the following propositions must also follow if the logic is to follow:

1. If wages and prices fall at the same rate, then labour productivity has to rise and employment remain constant or grow.

2. If wages and prices fall at the same rate, then labour productivity has to rise and employment must grow.

3. If wages and prices fall at the same rate, then labour productivity has to rise and what happens to employment is irrelevant.

4. None of the above.

The correct answer is:

If wages and prices fall at the same rate, then labour productivity has to rise and what happens to employment is irrelevant.

The EMU countries cannot improve their international competitiveness by exchange rate depreciation, which is the option always available to a fully sovereign nation issuing its own currency and floating it in foreign exchange markets.

Thus, to improve their international competitiveness, the EMU countries have to engage in “internal devaluation” which means they have to cut real unit labour costs – which are the real cost of producing goods and services. Governments setting out on this policy path have to engineer cuts in the wage and price levels (the latter following the former as unit costs fall).

But the question demonstrates that it takes more than just a nominal deflation. The strategy hinges on whether you can also engineer productivity growth (typically).

So given the assumption (wage and prices falling at the same rate), the correct answer is:

If wages and prices fall at the same rate, then labour productivity has to rise and what happens to employment is irrelevant.

Some explanatory notes to accompany the analysis that follows:

• Employment is measured in persons (averaged over the period).
• Labour productivity is the units of output per person employment per period.
• The wage and price level are in nominal units; the real wage is the wage level divided by the price level and tells us the real purchasing power of that nominal wage level.
• The wage bill is employment times the wage level and is the total labour costs in production for each period.
• Real GDP is thus employment times labour productivity and represents a flow of actual output per period; Nominal GDP is Real GDP at market value – that is, multiplied by the price level. So real GDP can grow while nominal GDP can fall if the price level is deflating and productivity growth and/or employment growth is positive.
• The wage share is the share of total wages in nominal GDP and is thus a guide to the distribution of national income between wages and profits.
• Unit labour costs are in nominal terms and are calculated as total labour costs divided by nominal GDP. So they tell you what each unit of output is costing in labour outlays; Real unit labour costs just divide this by the price level to give a real measure of what each unit of output is costing. RULC is also the ratio of the real wage to labour productivity and through algebra I would be able to show you (trust me) that it is equivalent to the Wage share measure (although I have expressed the latter in percentage terms and left the RULC measure in raw units).

The following table models the constant and growing productivity cases but holds employment constant for five periods. We assume that the nominal wage and the price level deflate by 10 per cent per period over Period 2 to 5. In the productivity growth case, we assume it grows by 10 per cent per period over Period 2 to 5.

It is quite clear that under the assumptions employed, RULC cannot fall without productivity growth. The only other way to accomplish this is to ensure that nominal wages fall faster than the price level falls. In the historical debate, this was a major contention between Keynes and Pigou (an economist in the neo-classical tradition who best represented the so-called “British Treasury View” in the 1930s. The Treasury View thought the cure to the Great Depression was to cut the real wage because according to their erroneous logic, unemployment could only occur if the real wage was too high.

Keynes argued that if you tried to cut nominal wages as a way of cutting the real wage (given there is no such thing as a real wage that policy can directly manipulate), firms will be forced by competition to cut prices to because unit labour costs would be lower. He hypothesised that there is no reason not to believe that the rate of deflation in nominal wage and price level would be similar and so the real wage would be constant over the period of the deflation. So that is the operating assumption here.

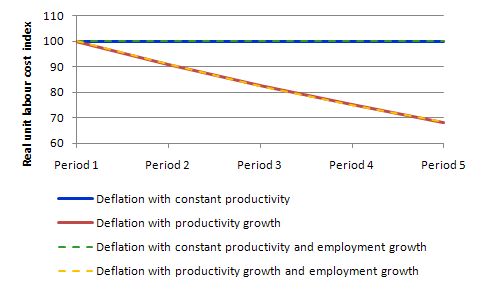
The following table models the constant and growing productivity cases as above but allows employment to grow by 10 per cent per period. All four scenarios in the Table are them modelled in the following graph with the Real Unit Labour Costs converted into index number form equal to 100 in Period 1. As you can see what happens to employment makes no difference at all.

I could have also modelled employment falling with the same results.

The following graph shows the four scenarios shown in the last two tables. I have dashed some scenarios to make the lines visible (given that Case A and Case C) are equivalent as are Case B and Case D. What you learn is that if wages and prices fall at the same rate and labour productivity does not rise there can be no reduction in unit or real unit labour costs.

So the internal devaluation strategy relies heavily on productivity growth occurring. The literature on organisational psychology and industrial relations is replete of examples where worker morale is an important ingredient in accomplishing productivity growth. In a climate of austerity characteristic of an internal devaluation strategy it is highly likely that productivity will not grow and may even fall over time. Then the internal devaluation strategy is useless.

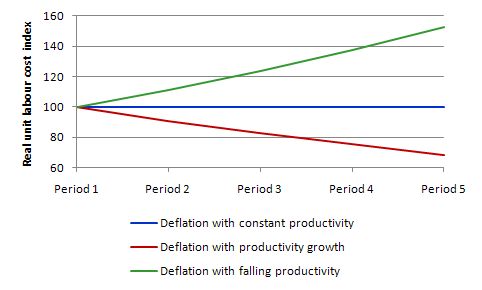
This graph compares the two scenarios in the first Table with the more realistic one that labour productivity actually falls as the government ravages the economy in pursuit of its internal devaluation. As you can see real unit labour costs rise as labour productivity falls and the economy’s competitiveness (given the exchange rate is fixed) falls.

Of-course, this “supply-side” scenario does not take into account the overwhelming reality that for an economy to realise this level of output over an extended period aggregate demand would have to be supportive. The internal devaluation strategy relies heavily on the external sector providing the demand impetus.

Given that Eurozone trade is heavily internal, it seems far fetched to assume that the trade impact arising from any successful internal devaluation will be sufficient to overcome the devastating domestic contraction in demand that will almost certainly occur. This is why commentators are calling for a domestic expansion in Germany to boost aggregate demand throughout the EMU, given the dominance of the German economy in the overall European trade.

That is clearly unlikely to happen given Germany has been engaged in a lengthy process of internal devaluation itself and the Government is resistant to any stimulus packages that might improve things within Germany and beyond via the trade impacts.

The following blogs may be of further interest to you:

• Euro zone’s self-imposed meltdown
• A Greek tragedy …
• España se está muriendo
• Exiting the Euro?
• Doomed from the start
• Europe – bailout or exit?
• Not the EMF … anything but the EMF!
• EMU posturing provides no durable solution
• Protect your workers for the sake of the nation
• The bullies and the bullied
• Modern monetary theory in an open economy

That is enough for today!

(c) Copyright 2018 William Mitchell. All Rights Reserved.