Saturday Quiz – February 16, 2013 – answers and discussion

Here are the answers with discussion for yesterday’s quiz. The information provided should help you understand the reasoning behind the answers. If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

Unlike a household which not only has to service its debt obligations over the course of the loan but also has to repay them at the due date, a national government debt, which issues its own currency can always roll over its “own currency” debt obligations and never has to pay them back.

The answer is False.

As a matter of clarification, note we are discussing debt issued in the currency of issue and not debt denominated in foreign currencies.

First, households do have to service their debts and repay them at some due date or risk default. The other crucial point is that households also have to forego some current consumption, use up savings or run down assets to service their debts and ultimately repay them.

Second, a sovereign government also has to service their debts and repay them at some due date or risk default. There is no difference there. The crucial difference is that unlike a household it does not have to forego any current spending capacity (or privatise public assets) to accomplish these financial transactions.

But the public debt is a legal obligation on government and so is a liability that has to be managed.

Now can it just roll-it over continuously? Well the question was subtle because the government can always keep issuing new debt when the old issues mature. But as the previous debt-issued matures it is paid out as per the terms of the issue.

The other point is that the liability on a sovereign government is legally like all liabilities – enforceable in courts the risk associated with taking that liability on is zero which is very different to the risks attached to taking on private debt.

There is zero financial risk that a holder of a public bond instrument will not be paid principle and interest on time.

The other point to appreciate is that the original holder of the public debt might not be the final holder who is paid out. The market for public debt is the most liquid of all debt markets and trading in public debt instruments of all nations is conducted across all markets each hour of every day.

While I am most familiar with the Australian institutional structure, the following developments are not dissimilar to the way bond issuance (in primary markets) is organised elsewhere. You can access information about this from the Australian Office of Financial Management, which is a Treasury-related public body that manages all public debt issuance in Australia.

It conducts the primary market, which is the institutional machinery via which the government sells debt to the non-government sector. In a modern monetary system with flexible exchange rates it is clear the government does not have to finance its spending so the fact that governments hang on to primary market issuance is largely ideological – fear of fiscal excesses rather than an intrinsic need. In this blog – Will we really pay higher interest rates? – I go into this period more fully and show that it was driven by the ideological calls for “fiscal discipline” and the growing influence of the credit rating agencies. Accordingly, all net spending had to be fully placed in the private market $-for-$. A purely voluntary constraint on the government and a waste of time.

A secondary market is where existing financial assets are traded by interested parties. So the financial assets enter the monetary system via the primary market and are then available for trading in the secondary. The same structure applies to private share issues for example. The company raises funds via the primary issuance process then its shares are traded in secondary markets.

Clearly secondary market trading has no impact at all on the volume of financial assets in the system – it just shuffles the wealth between wealth-holders. In the context of public debt issuance – the transactions in the primary market are vertical (net financial assets are created or destroyed) and the secondary market transactions are all horizontal (no new financial assets are created). Please read my blog – Deficit spending 101 – Part 3 – for more information.

Primary issues are conducted via auction tender systems and the Treasury determines the timing of these events in addition to the type and volumne of debt to be issued.

The issue is then be put out for tender and the market determines the final price of the bonds issued. Imagine a $A1000 bond is offered at a coupon of 5 per cent, meaning that you would get $A50 dollar per annum until the bond matured at which time you would get $A1000 back.

Imagine that the market wanted a yield of 6 per cent to accommodate risk expectations (see below). So for them the bond is unattractive unless the price is lower than $A1000. So tender system they would put in a purchase bid lower than the $A1000 to ensure they get the 6 per cent return they sought.

The general rule for fixed-income bonds is that when the prices rise, the yield falls and vice versa. Thus, the price of a bond can change in the market place according to interest rate fluctuations.

When interest rates rise, the price of previously issued bonds fall because they are less attractive in comparison to the newly issued bonds, which are offering a higher coupon rates (reflecting current interest rates).

When interest rates fall, the price of older bonds increase, becoming more attractive as newly issued bonds offer a lower coupon rate than the older higher coupon rated bonds.

So for new bond issues the AOFM receives the tenders from the bond market traders. These will be ranked in terms of price (and implied yields desired) and a quantity requested in $ millions. The AOFM (which is really just part of treasury) sometimes sells some bonds to the central bank (RBA) for their open market operations (at the weighted average yield of the final tender).

The AOFM will then issue the bonds in highest price bid order until it raises the revenue it seeks. So the first bidder with the highest price (lowest yield) gets what they want (as long as it doesn’t exhaust the whole tender, which is not likely). Then the second bidder (higher yield) and so on.

In this way, if demand for the tender is low, the final yields will be higher and vice versa. There are a lot of myths peddled in the financial press about this. Rising yields may indicate a rising sense of risk (mostly from future inflation although sovereign credit ratings will influence this). But they may also indicated a recovering economy where people are more confidence investing in commercial paper (for higher returns) and so they demand less of the “risk free” government paper.

So while there is no credit risk attached to holding public debt (that is, the holder knows they will receive the principle and interest that is specified on the issued debt instrument), there is still market risk which is related to movements in interest rates.

For government accounting purposes however the trading of the bonds once issued is of no consequence. They still retain the liability to pay the fixed coupon rate and the face value of the bond at the time of issue (not the market price).

The person/institution that sells the bond before maturity may gain or lose relative to their original purchase price but that is totally outside of the concern of the government.

Its liability is to pay the specified coupon rate at the time of issue and then the whole face value at the time of maturity.

There are complications to the primary sale process – some bonds sell at discounts which imply the coupon value. Further, there are arrangements between treasuries and central banks about the way in which public debt holdings are managed and accounted for. But these nuances do not alter the initial contention – public debt is a liability of the government in just the same way as private debt is a liability for those holders.

The following blogs may be of further interest to you:

• Time to outlaw the credit rating agencies
• Will we really pay higher interest rates?

Question 2:

Standing facilities that central banks maintain means that the monetary base always adjusts to the changes in the money supply.

The answer is True.

This question challenges the notion of the money multiplier which is a central concept in mainstream macroeconomics textbooks.

They posit that the multiplier m transmits changes in the so-called monetary base (MB) (the sum of bank reserves and currency at issue) into changes in the money supply (M).

Students rehearse several times in their undergraduate courses (introductory and intermediate macroeconomics; money and banking; monetary economics etc) the mantra that the money multiplier is usually expressed as the inverse of the required reserve ratio plus some other novelties relating to preferences for cash versus deposits by the public.

Accordingly, the students learn that if the central bank told private banks that they had to keep 10 per cent of total deposits as reserves then the required reserve ratio (RRR) would be 0.10 and m would equal 1/0.10 = 10. More complicated formulae are derived when you consider that people also will want to hold some of their deposits as cash. But these complications do not add anything to the story.

The formula for the determination of the money supply is: M = m x MB. So if a $1 is newly deposited in a bank, the money supply will rise (be multiplied) by $10 (if the RRR = 0.10). The way this multiplier is alleged to work is explained as follows (assuming the bank is required to hold 10 per cent of all deposits as reserves):

• A person deposits say $100 in a bank.
• To make money, the bank then loans the remaining $90 to a customer.
• They spend the money and the recipient of the funds deposits it with their bank.
• That bank then lends 0.9 times $90 = $81 (keeping 0.10 in reserve as required).
• And so on until the loans become so small that they dissolve to zero

None of this captures the way banks make loans. It is an important device for the mainstream because it implies that banks take deposits to get funds which they can then on-lend. But prudential regulations require they keep a little in reserve. So we get this credit creation process ballooning out due to the fractional reserve requirements.

The money multiplier myth also leads students to think that as the central bank can control the monetary base then it can control the money supply. Further, given that inflation is allegedly the result of the money supply growing too fast then the blame is sheeted hometo the “government”. This leads to claims that if the government runs a budget deficit then it has to issue bonds to avoid causing hyperinflation. Nothing could be further from the truth.

That is nothing like the way the banking system operates in the real world. The idea that the monetary base (the sum of bank reserves and currency) leads to a change in the money supply via some multiple is not a valid representation of the way the monetary system operates.

First, the central bank does not have the capacity to control the money supply in a modern monetary system. In the world we live in, bank loans create deposits and are made without reference to the reserve positions of the banks. The bank then ensures its reserve positions are legally compliant as a separate process knowing that it can always get the reserves from the central bank. The only way that the central bank can influence credit creation in this setting is via the price of the reserves it provides on demand to the commercial banks.

Second, this suggests that the decisions by banks to lend may be influenced by the price of reserves rather than whether they have sufficient reserves. They can always get the reserves that are required at any point in time at a price, which may be prohibitive.

Third, the money multiplier story has the central bank manipulating the money supply via open market operations. So they would argue that the central bank might buy bonds to the public to increase the money base and then allow the fractional reserve system to expand the money supply. But a moment’s thought will lead you to conclude this would be futile unless (as in Question 3 a support rate on excess reserves equal to the current policy rate was being paid).

Why? The open market purchase would increase bank reserves and the commercial banks, in lieu of any market return on the overnight funds, would try to place them in the interbank market. Of-course, any transactions at this level (they are horizontal) net to zero so all that happens is that the excess reserve position of the system is shuffled between banks. But in the process the interbank return would start to fall and if the process was left to resolve, the overnight rate would fall to zero and the central bank would lose control of its monetary policy position (unless it was targetting a zero interest rate).

In lieu of a support rate equal to the target rate, the central bank would have to sell bonds to drain the excess reserves. The same futility would occur if the central bank attempted to reduce the money supply by instigating an open market sale of bonds.

In all cases, the central bank cannot influence the money supply in this way.

Fourth, given that the central bank adds reserves on demand to maintain financial stability and this process is driven by changes in the money supply as banks make loans which create deposits.

So the operational reality is that the dynamics of the monetary base (MB) are driven by the changes in the money supply which is exactly the reverse of the causality presented by the monetary multiplier.

So in fact we might write MB = M/m.

You might like to read these blogs for further information:

• Teaching macroeconomics students the facts
• Lost in a macroeconomics textbook again
• Lending is capital- not reserve-constrained
• Oh no … Bernanke is loose and those greenbacks are everywhere
• Building bank reserves will not expand credit
• Building bank reserves is not inflationary
• 100-percent reserve banking and state banks
• Money multiplier and other myths

Question 3:

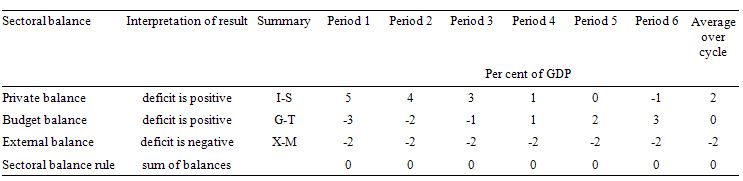
Assume that the current account deficit of a nation is stable and equal to 2 per cent of GDP throughout a complete business cycle. The government is imposing fiscal austerity and at a particular point over that cycle we observe a government surplus equal to 3 per cent of GDP but which over the complete business cycle will end up being balanced. We also would know two things about the private domestic sector balance – at the observation point and on average over the cycle. It would be in:

(a) deficit by 5 per cent of GDP but on average over the cycle in surplus equal to 2 per cent of GDP.

(b) deficit by 5 per cent of GDP but on average over the cycle in deficit equal to 2 per cent of GDP.

(c) deficit by 1 per cent of GDP but on average over the cycle in surplus equal to 2 per cent of GDP.

(d) deficit by 1 per cent of GDP but on average over the cycle in deficit equal to 2 per cent of GDP.

The answer is Option (b) – deficit by 5 per cent of GDP but on average over the cycle in deficit equal to 2 per cent of GDP.

Note that this question doesn’t investigate how the economy might get into this situation. But whatever behavioural forces were at play, the sectoral balances all have to sum to zero. Once you understand that, then deduction leads to the correct answer.

To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

From the uses perspective, national income (GDP) can be used for:

GDP = C + S + T

which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.

Equating these two perspectives we get:

C + S + T = GDP = C + I + G + (X – M)

So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.

(I – S) + (G – T) + (X – M) = 0

That is the three balances have to sum to zero. The sectoral balances derived are:

• The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
• The Budget Deficit (G – T) – negative if in surplus, positive if in deficit.
• The Current Account balance (X – M) – positive if in surplus, negative if in deficit.

These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.

A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).

This is also a basic rule derived from the national accounts and has to apply at all times.

To help us answer the specific question posed, the following Table shows a stylised business cycle with some simplifications. The economy is running a surplus in the first three periods (but declining) and then increasing deficits. Over the entire cycle the balanced budget rule would be achieved as the budget balances average to zero. So the deficits are covered by fully offsetting surpluses over the cycle.

The simplification is the constant external deficit (that is, no cyclical sensitivity) of 2 per cent of GDP over the entire cycle. You can then see what the private domestic balance is doing clearly. When the budget balance is in surplus, the private balance is in deficit. The larger the budget surplus the larger the private deficit for a given external deficit.

As the budget moves into deficit, the private domestic balance approaches balance and then finally in Period 6, the budget deficit is large enough (3 per cent of GDP) to offset the demand-draining external deficit (2 per cent of GDP) and so the private domestic sector can save overall. The budget deficits are underpinning spending and allowing income growth to be sufficient to generate savings greater than investment in the private domestic sector.

Period 1 refers to our observation point (a surplus of 3 per cent of GDP, an external deficit of 2 per cent of GDP and a private domestic deficit of 4 per cent of GDP).

On average over the cycle, under these conditions (balanced public budget) the private domestic deficit exactly equals the external deficit. As a result over the course of the business cycle, the private domestic sector is spending more than it is earning. This could be via increasing indebtedness or running down previous savings or asset accumulation.

The following blogs may be of further interest to you:

• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!