Saturday Quiz – September 14, 2013 – answers and discussion

Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

If workers succeed in gaining real wages increases then, other things equal, the share of profits in national income is squeezed.

The answer is False.

The question requires you to understand what determines the real wage and what the relationship between earnings and labour productivity growth is. When economists do not specify the unit you should always assume they are talking in nominal terms. So the reference to the “rate of growth of earnings” is in terms of the monetary unit which is the common understanding that people would have of the term.

In terms of the logic of the question, that would also be the only sensible interpretation.

The real wage is defined as the purchasing power equivalent on the nominal wage that workers get paid each period. To compute the real wage we need to consider two variables: (a) the nominal wage (W) and the aggregate price level (P).

We might consider the aggregate price level to be measured by the consumer price index (CPI) although there are huge debates about that. But in a sense, this macroeconomic price level doesn’t exist but represents some abstract measure of the general movement in all prices in the economy.

Macroeconomics is hard to learn because it involves these abstract variables that are never observed – like the price level, like “the interest rate” etc. They are just stylisations of the general tendency of all the different prices and interest rates.

Now the nominal wage (W) – that is paid by employers to workers is determined in the labour market – by the contract of employment between the worker and the employer. The price level (P) is determined in the goods market – by the interaction of total supply of output and aggregate demand for that output although there are complex models of firm price setting that use cost-plus mark-up formulas with demand just determining volume sold. We shouldn’t get into those debates here.

The inflation rate is just the continuous growth in the price level (P). A once-off adjustment in the price level is not considered by economists to constitute inflation.

So the real wage (w) tells us what volume of real goods and services the nominal wage (W) will be able to command and is obviously influenced by the level of W and the price level. For a given W, the lower is P the greater the purchasing power of the nominal wage and so the higher is the real wage (w).

We write the real wage (w) as W/P. So if W = 10 and P = 1, then the real wage (w) = 10 meaning that the current wage will buy 10 units of real output. If P rose to 2 then w = 5, meaning the real wage was now cut by one-half.

The relationship between the real wage and labour productivity relates to movements in the unit costs, real unit labour costs and the wage and profit shares in national income.

The wage share in nominal GDP is expressed as the total wage bill as a percentage of nominal GDP. Economists differentiate between nominal GDP ($GDP), which is total output produced at market prices and real GDP (GDP), which is the actual physical equivalent of the nominal GDP. We will come back to that distinction soon.

To compute the wage share we need to consider total labour costs in production and the flow of production ($GDP) each period.

Employment (L) is a stock and is measured in persons (averaged over some period like a month or a quarter or a year.

The wage bill is a flow and is the product of total employment (L) and the average wage (w) prevailing at any point in time. Stocks (L) become flows if it is multiplied by a flow variable (W). So the wage bill is the total labour costs in production per period.

So the wage bill = W.L

The wage share is just the total labour costs expressed as a proportion of $GDP – (W.L)/$GDP in nominal terms, usually expressed as a percentage. We can actually break this down further.

Labour productivity (LP) is the units of real GDP per person employed per period. Using the symbols already defined this can be written as:

LP = GDP/L

so it tells us what real output (GDP) each labour unit that is added to production produces on average.

Nominal GDP ($GDP) can be written as P.GDP, where the P values the real physical output.

Now if you put of these concepts together you get an interesting framework. To help you follow the logic here are the terms developed and be careful not to confuse $GDP (nominal) with GDP (real):

• Wage share = (W.L)/$GDP
• Nominal GDP: $GDP = P.GDP
• Labour productivity: LP = GDP/L
• Real wage: w = W/P

By substituting the expression for Nominal GDP into the wage share measure we get:

Wage share = (W.L)/P.GDP

In this area of economics, we often look for alternative way to write this expression – it maintains the equivalence (that is, obeys all the rules of algebra) but presents the expression (in this case the wage share) in a different “view”.

So we can write as an equivalent:

Wage share – (W/P).(L/GDP)

Now if you note that (L/GDP) is the inverse (reciprocal) of the labour productivity term (GDP/L). We can use another rule of algebra (reversing the invert and multiply rule) to rewrite this expression again in a more interpretable fashion.

So an equivalent but more convenient measure of the wage share is:

Wage share = (W/P)/(GDP/L) – that is, the real wage (W/P) divided by labour productivity (GDP/L).

I won’t show this but I could also express this in growth terms such that if the growth in the real wage equals labour productivity growth the wage share is constant. The algebra is simple but we have done enough of that already.

That journey might have seemed difficult to non-economists (or those not well-versed in algebra) but it produces a very easy to understand formula for the wage share.

Two other points to note. The wage share is also equivalent to the real unit labour cost (RULC) measures that Treasuries and central banks use to describe trends in costs within the economy. Please read my blog – Saturday Quiz – May 15, 2010 – answers and discussion – for more discussion on this point.

Now it becomes obvious that if the nominal wage (W) and the price level (P) are growing at the pace the real wage is constant. And if the real wage is growing at the same rate as labour productivity, then both terms in the wage share ratio are equal and so the wage share is constant.

The wage share was constant for a long time during the Post Second World period and this constancy was so marked that Kaldor (the Cambridge economist) termed it one of the great “stylised” facts. So real wages grew in line with productivity growth which was the source of increasing living standards for workers.

The productivity growth provided the “room” in the distribution system for workers to enjoy a greater command over real production and thus higher living standards without threatening inflation.

Since the mid-1980s, the neo-liberal assault on workers’ rights (trade union attacks; deregulation; privatisation; persistently high unemployment) has seen this nexus between real wages and labour productivity growth broken. So while real wages have been stagnant or growing modestly, this growth has been dwarfed by labour productivity growth.

The following blogs may be of further interest to you:

• The origins of the economic crisis
• The fiscal stimulus worked but was captured by profits

Question 2:

Government spending can crowd out private spending, which means that an increase in the former will reduce the latter.

The answer is True.

The question explores the differences between “real crowding out” and the more commonly-used notion (by mainstream economists) of “financial crowding out”.

The normal presentation of the crowding out hypothesis which is a central plank in the mainstream economics attack on government fiscal intervention is more accurately called “financial crowding out”.

At the heart of this conception is the theory of loanable funds, which is a aggregate construction of the way financial markets are meant to work in mainstream macroeconomic thinking. The original conception was designed to explain how aggregate demand could never fall short of aggregate supply because interest rate adjustments would always bring investment and saving into equality.

In Mankiw, which is representative, we are taken back in time, to the theories that were prevalent before being destroyed by the intellectual advances provided in Keynes’ General Theory. Mankiw assumes that it is reasonable to represent the financial system as the “market for loanable funds” where “all savers go to this market to deposit their savings, and all borrowers go to this market to get their loans. In this market, there is one interest rate, which is both the return to saving and the cost of borrowing.”

This is back in the pre-Keynesian world of the loanable funds doctrine (first developed by Wicksell).

This doctrine was a central part of the so-called classical model where perfectly flexible prices delivered self-adjusting, market-clearing aggregate markets at all times. If consumption fell, then saving would rise and this would not lead to an oversupply of goods because investment (capital goods production) would rise in proportion with saving. So while the composition of output might change (workers would be shifted between the consumption goods sector to the capital goods sector), a full employment equilibrium was always maintained as long as price flexibility was not impeded. The interest rate became the vehicle to mediate saving and investment to ensure that there was never any gluts.

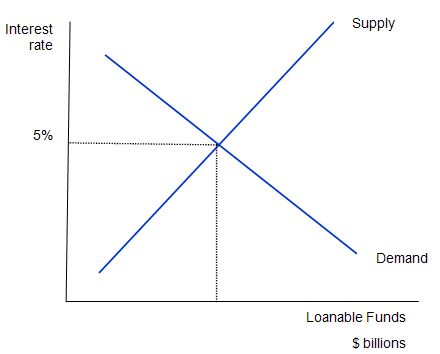
The following diagram shows the market for loanable funds. The current real interest rate that balances supply (saving) and demand (investment) is 5 per cent (the equilibrium rate). The supply of funds comes from those people who have some extra income they want to save and lend out. The demand for funds comes from households and firms who wish to borrow to invest (houses, factories, equipment etc). The interest rate is the price of the loan and the return on savings and thus the supply and demand curves (lines) take the shape they do.

Note that the entire analysis is in real terms with the real interest rate equal to the nominal rate minus the inflation rate. This is because inflation “erodes the value of money” which has different consequences for savers and investors.

Mankiw claims that this “market works much like other markets in the economy” and thus argues that (p. 551):

The adjustment of the interest rate to the equilibrium occurs for the usual reasons. If the interest rate were lower than the equilibrium level, the quantity of loanable funds supplied would be less than the quantity of loanable funds demanded. The resulting shortage … would encourage lenders to raise the interest rate they charge.

The converse then follows if the interest rate is above the equilibrium.

Mankiw also says that the “supply of loanable funds comes from national saving including both private saving and public saving.” Think about that for a moment. Clearly private saving is stockpiled in financial assets somewhere in the system – maybe it remains in bank deposits maybe not. But it can be drawn down at some future point for consumption purposes.

Mankiw thinks that budget surpluses are akin to this. They are not even remotely like private saving. They actually destroy liquidity in the non-government sector (by destroying net financial assets held by that sector). They squeeze the capacity of the non-government sector to spend and save. If there are no other behavioural changes in the economy to accompany the pursuit of budget surpluses, then as we will explain soon, income adjustments (as aggregate demand falls) wipe out non-government saving.

So this conception of a loanable funds market bears no relation to “any other market in the economy” despite the myths that Mankiw uses to brainwash the students who use the book and sit in the lectures.

Also reflect on the way the banking system operates – read Money multiplier and other myths if you are unsure. The idea that banks sit there waiting for savers and then once they have their savings as deposits they then lend to investors is not even remotely like the way the banking system works.

This framework is then used to analyse fiscal policy impacts and the alleged negative consquences of budget deficits – the so-called financial crowding out – is derived.

Mankiw says:

One of the most pressing policy issues … has been the government budget deficit … In recent years, the U.S. federal government has run large budget deficits, resulting in a rapidly growing government debt. As a result, much public debate has centred on the effect of these deficits both on the allocation of the economy’s scarce resources and on long-term economic growth.

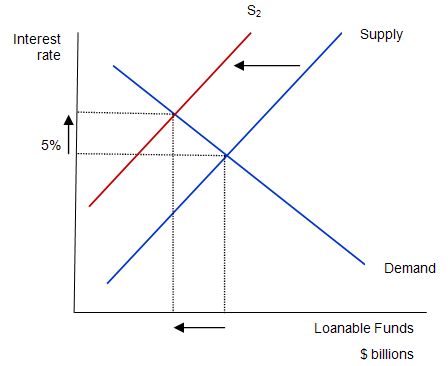
So what would happen if there is a budget deficit. Mankiw asks: “which curve shifts when the budget deficit rises?”

Consider the next diagram, which is used to answer this question. The mainstream paradigm argue that the supply curve shifts to S₂. Why does that happen? The twisted logic is as follows: national saving is the source of loanable funds and is composed (allegedly) of the sum of private and public saving. A rising budget deficit reduces public saving and available national saving. The budget deficit doesn’t influence the demand for funds (allegedly) so that line remains unchanged.

The claimed impacts are: (a) “A budget deficit decreases the supply of loanable funds”; (b) “… which raises the interest rate”; (c) “… and reduces the equilibrium quantity of loanable funds”.

Mankiw says that:

The fall in investment because of the government borrowing is called crowding out …That is, when the government borrows to finance its budget deficit, it crowds out private borrowers who are trying to finance investment. Thus, the most basic lesson about budget deficits … When the government reduces national saving by running a budget deficit, the interest rate rises, and investment falls. Because investment is important for long-run economic growth, government budget deficits reduce the economy’s growth rate.

The analysis relies on layers of myths which have permeated the public space to become almost “self-evident truths”. Sometimes, this makes is hard to know where to start in debunking it. Obviously, national governments are not revenue-constrained so their borrowing is for other reasons – we have discussed this at length. This trilogy of blogs will help you understand this if you are new to my blog – Deficit spending 101 – Part 1 | Deficit spending 101 – Part 2 | Deficit spending 101 – Part 3.

But governments do borrow – for stupid ideological reasons and to facilitate central bank operations – so doesn’t this increase the claim on saving and reduce the “loanable funds” available for investors? Does the competition for saving push up the interest rates?

The answer to both questions is no! Modern Monetary Theory (MMT) does not claim that central bank interest rate hikes are not possible. There is also the possibility that rising interest rates reduce aggregate demand via the balance between expectations of future returns on investments and the cost of implementing the projects being changed by the rising interest rates.

MMT proposes that the demand impact of interest rate rises are unclear and may not even be negative depending on rather complex distributional factors. Remember that rising interest rates represent both a cost and a benefit depending on which side of the equation you are on. Interest rate changes also influence aggregate demand – if at all – in an indirect fashion whereas government spending injects spending immediately into the economy.

But having said that, the Classical claims about crowding out are not based on these mechanisms. In fact, they assume that savings are finite and the government spending is financially constrained which means it has to seek “funding” in order to progress their fiscal plans. The result competition for the “finite” saving pool drives interest rates up and damages private spending. This is what is taught under the heading “financial crowding out”.

A related theory which is taught under the banner of IS-LM theory (in macroeconomic textbooks) assumes that the central bank can exogenously set the money supply. Then the rising income from the deficit spending pushes up money demand and this squeezes interest rates up to clear the money market. This is the Bastard Keynesian approach to financial crowding out.

Neither theory is remotely correct and is not related to the fact that central banks push up interest rates up because they believe they should be fighting inflation and interest rate rises stifle aggregate demand.

However, other forms of crowding out are possible. In particular, MMT recognises the need to avoid or manage real crowding out which arises from there being insufficient real resources being available to satisfy all the nominal demands for such resources at any point in time.

In these situation, the competing demands will drive inflation pressures and ultimately demand contraction is required to resolve the conflict and to bring the nominal demand growth into line with the growth in real output capacity.

Further, while there is mounting hysteria about the problems the changing demographics will introduce to government budgets all the arguments presented are based upon spurious financial reasoning – that the government will not be able to afford to fund health programs (for example) and that taxes will have to rise to punitive levels to make provision possible but in doing so growth will be damaged.

However, MMT dismisses these “financial” arguments and instead emphasises the possibility of real problems – a lack of productivity growth; a lack of goods and services; environment impingements; etc.

Then the argument can be seen quite differently. The responses the mainstream are proposing (and introducing in some nations) which emphasise budget surpluses (as demonstrations of fiscal discipline) are shown by MMT to actually undermine the real capacity of the economy to address the actual future issues surrounding rising dependency ratios. So by cutting funding to education now or leaving people unemployed or underemployed now, governments reduce the future income generating potential and the likely provision of required goods and services in the future.

The idea of real crowding out also invokes and emphasis on political issues. If there is full capacity utilisation and the government wants to increase its share of full employment output then it has to crowd the private sector out in real terms to accomplish that. It can achieve this aim via tax policy (as an example). But ultimately this trade-off would be a political choice – rather than financial.

Question 3:

Suppose that the government announced it intended to cut its deficit from 4 per cent of GDP to 2 per cent in the coming year and during that year net exports were projected to move from a deficit of 1 per cent of GDP to a surplus of 1 per cent of GDP. If private sector deleveraging resulted in it spending less than it earned to the measure of 5 per cent of GDP, then the fiscal austerity plans will undermine growth even if the net export surplus was realised.

The answer is True.

This question requires an understanding of the sectoral balances that can be derived from the National Accounts. But it also requires some understanding of the behavioural relationships within and between these sectors which generate the outcomes that are captured in the National Accounts and summarised by the sectoral balances.

From an accounting sense, if the external sector goes into surplus (positive net exports) there is scope for the government balance to move into surplus without compromising growth as long as the external position (injection of spending) more than offsets any actual private domestic sector net saving.

In that sense, the strategy requires net exports adding more to aggregate demand than is destroyed by the government via its fiscal austerity. But it also implicitly assumes the private domestic sector will not undermine the strategy via increased saving overall.

Skip the next section explaining the balances if you are familiar with the derivation. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced.

Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

From the uses perspective, national income (GDP) can be used for:

GDP = C + S + T

which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.

Equating these two perspectives we get:

C + S + T = GDP = C + I + G + (X – M)

So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.

(I – S) + (G – T) + (X – M) = 0

That is the three balances have to sum to zero. The sectoral balances derived are:

• The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
• The Budget Deficit (G – T) – negative if in surplus, positive if in deficit.
• The Current Account balance (X – M) – positive if in surplus, negative if in deficit.

These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.

A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).

This is also a basic rule derived from the national accounts and has to apply at all times.

If the nation is running an external surplus it means that the contribution to aggregate demand from the external sector is positive – that is net spending injection – providing a boost to domestic production and income generation.

The extent to which this allows the government to reduce its deficit (by the same amount as the run a surplus equal to the external balance and not endanger growth depends on the private domestic sector’s spending decisions (overall). If the private domestic sector runs a deficit, then the EU/IMF/ECB strategy will work under the assumed conditions – inasmuch as the goal is to reduce the budget deficit without compromising growth.

But this strategy would be unsustainable as it would require the private domestic sector overall to continually increase its indebtedness.

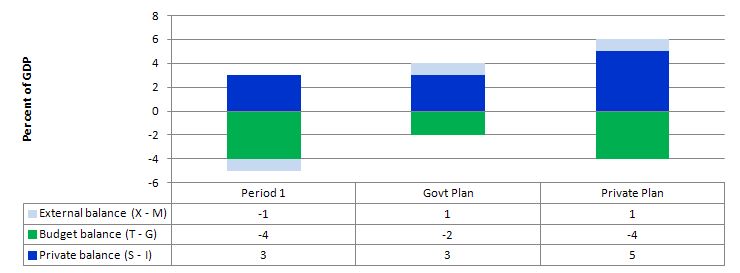
The following graph captures what might happen if the private domestic sector (households and firms) seeks to increase its overall saving at the same time the net exports are rising and the government deficit is falling.

In Period 1, there is an external deficit of 1 per cent of GDP and a budget deficit of 4 per cent of GDP which generates income sufficient to allow the private domestic sector to save 3 per cent of GDP.

The Government plans to cut its deficit to 2 per cent of GDP by cutting spending. To achieve that at the same time that net exports is rising to 1 per cent of GDP then the government would be implicitly assuming that the private domestic sector would not change its saving behaviour overall.

However, what happens if the private sector, fearing the contractionary forces coming from the announced cuts in public spending and not really being in a position to assess what might happen to net exports over the coming period, decides to increase its saving. In other words, they plan to increase net saving to 5 per cent of GDP – the situation captured under the Private Plan option.

In this case, if the private sector actually succeeded in reducing its spending and increasing its saving balance to 5 per cent of GDP, the income shifts would ensure the government could not realise its planned deficit reduction.

The public and private plans are clearly not compatible and the resolution of their competing objectives would be achieved by income shifts.

In other words, as the private sector and the public sector reduced their spending in pursuit of their plans, income would contract even though net exports were rising.

The situation is that unless private sector behaviour remains constant the government cannot rely on an increase in net exports to provide the space for them to cut their own net spending.

So in general, with the government contracting the only way the private domestic sector could successfully increase its net saving is if the injection from the external sector offsett the drain from the domestic sector (public and private). Otherwise, income will decline and both the government and private domestic sector will find it difficult to reduce their net spending positions.

Take a balanced budget position, then income will decline unless the private domestic sector’s saving overall is just equal to the external surplus. If the private domestic sector tried to push its position further into surplus then the following story might unfold.

Consistent with this aspiration, households may cut back on consumption spending and save more out of disposable income. The immediate impact is that aggregate demand will fall and inventories will start to increase beyond the desired level of the firms.

The firms will soon react to the increased inventory holding costs and will start to cut back production. How quickly this happens depends on a number of factors including the pace and magnitude of the initial demand contraction. But if the households persist in trying to save more and consumption continues to lag, then soon enough the economy starts to contract – output, employment and income all fall.

The initial contraction in consumption multiplies through the expenditure system as workers who are laid off also lose income and their spending declines. This leads to further contractions.

The declining income leads to a number of consequences. Net exports improve as imports fall (less income) but the question clearly assumes that the external sector remains in deficit. Total saving actually starts to decline as income falls as does induced consumption.

So the initial discretionary decline in consumption is supplemented by the induced consumption falls driven by the multiplier process.

The decline in income then stifles firms’ investment plans – they become pessimistic of the chances of realising the output derived from augmented capacity and so aggregate demand plunges further. Both these effects push the private domestic balance further towards and eventually into surplus

With the economy in decline, tax revenue falls and welfare payments rise which push the public budget balance towards and eventually into deficit via the automatic stabilisers.

If the private sector persists in trying to increase its saving ratio then the contracting income will clearly push the budget into deficit.

So the external position has to be sufficiently strong enough to offset the domestic drains on expenditure. For Greece at present that is clearly not the case and demonstrates why the EU/ECB/IMF strategy is failing.

The following blogs may be of further interest to you:

• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!