The Weekend Quiz – November 18-19, 2017 – answers and discussion

Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

Larger fiscal deficits as a percentage of GDP typically mean that there are less real resources available for other productive uses.

The answer is True.

It is clear that at any point in time, there are finite real resources available for production. New resources can be discovered, produced and the old stock spread better via education and productivity growth. The aim of production is to use these real resources to produce goods and services that people want either via private or public provision.

So by definition any sectoral claim (via spending) on the real resources reduces the availability for other users. There is always an opportunity cost involved in real terms when one component of spending increases relative to another.

Unless you subscribe to the extreme end of mainstream economics which espouses concepts such as 100 per cent crowding out via financial markets and/or Ricardian equivalence consumption effects, you will conclude that rising net public spending as percentage of GDP will add to aggregate demand and as long as the economy can produce more real goods and services in response, this increase in public demand will be met with increased public access to real goods and services.

You might also wonder whether it matters if the economy is already at full capacity. Under these conditions a rising public share of GDP must squeeze real usage by the non-government sector which might also drive inflation as the economy tries to siphon of the incompatible nominal demands on final real output.

You might say that the deficits might rise as a percentage of GDP as a result of a decline in private spending triggering the automatic stabilisers which would suggest many idle resources. That is clearly possible but doesn’t alter the fact that the public claims on the total resources available have risen.

Under these circumstances the opportunity costs involved are very low because of the excess capacity.
The question really seeks to detect whether you have been able to distinguish between the financial crowding out myth that is found in all the mainstream macroeconomics textbooks and concepts of real crowding out.

The normal presentation of the crowding out hypothesis which is a central plank in the mainstream economics attack on government fiscal intervention is more accurately called “financial crowding out”.

At the heart of this conception is the theory of loanable funds, which is a aggregate construction of the way financial markets are meant to work in mainstream macroeconomic thinking. The original conception was designed to explain how aggregate demand could never fall short of aggregate supply because interest rate adjustments would always bring investment and saving into equality.

At the heart of this erroneous hypothesis is a flawed viewed of financial markets. The so-called loanable funds market is constructed by the mainstream economists as serving to mediate saving and investment via interest rate variations.

This is pre-Keynesian thinking and was a central part of the so-called classical model where perfectly flexible prices delivered self-adjusting, market-clearing aggregate markets at all times. If consumption fell, then saving would rise and this would not lead to an oversupply of goods because investment (capital goods production) would rise in proportion with saving. So while the composition of output might change (workers would be shifted between the consumption goods sector to the capital goods sector), a full employment equilibrium was always maintained as long as price flexibility was not impeded. The interest rate became the vehicle to mediate saving and investment to ensure that there was never any gluts.

So saving (supply of funds) is conceived of as a positive function of the real interest rate because rising rates increase the opportunity cost of current consumption and thus encourage saving. Investment (demand for funds) declines with the interest rate because the costs of funds to invest in (houses, factories, equipment etc) rises.

Changes in the interest rate thus create continuous equilibrium such that aggregate demand always equals aggregate supply and the composition of final demand (between consumption and investment) changes as interest rates adjust.

According to this theory, if there is a rising fiscal deficit then there is increased demand is placed on the scarce savings (via the alleged need to borrow by the government) and this pushes interest rates to “clear” the loanable funds market. This chokes off investment spending.

So allegedly, when the government borrows to “finance” its fiscal deficit, it crowds out private borrowers who are trying to finance investment. The mainstream economists conceive of this as the government reducing national saving (by running a fiscal deficit) and pushing up interest rates which damage private investment.

The analysis relies on layers of myths which have permeated the public space to become almost self-evident truths. This trilogy of blogs will help you understand this if you are new to my blog – Deficit spending 101 – Part 1 – Deficit spending 101 – Part 2 – Deficit spending 101 – Part 3.

The basic flaws in the mainstream story are that governments just borrow back the net financial assets that they create when they spend. Its a wash! It is true that the private sector might wish to spread these financial assets across different portfolios. But then the implication is that the private spending component of total demand will rise and there will be a reduced need for net public spending.

Further, they assume that savings are finite and the government spending is financially constrained which means it has to seek “funding” in order to progress their fiscal plans. But government spending by stimulating income also stimulates saving.

The flawed notion of financial crowding out has to be distinguished from other forms of crowding out which are possible. In particular, MMT recognises the need to avoid or manage real crowding out which arises from there being insufficient real resources being available to satisfy all the nominal demands for such resources at any point in time.

In these situation, the competing demands will drive inflation pressures and ultimately demand contraction is required to resolve the conflict and to bring the nominal demand growth into line with the growth in real output capacity.

The idea of real crowding out also invokes and emphasis on political issues. If there is full capacity utilisation and the government wants to increase its share of full employment output then it has to crowd the private sector out in real terms to accomplish that. It can achieve this aim via tax policy (as an example). But ultimately this trade-off would be a political choice – rather than financial.

The following blogs may be of further interest to you:

• When a huge pack of lies is barely enough
• Saturday Quiz – April 17, 2010 – answers and discussion

Question 2:

For a nation running a current account deficit, national income adjustments will ensure government fiscal balance is in deficit if the private domestic sector seeks to increase its saving overall as a percentage of GDP.

The answer is True.

This question requires an understanding of the sectoral balances that can be derived from the National Accounts. But it also requires some understanding of the behavioural relationships within and between these sectors which generate the outcomes that are captured in the National Accounts and summarised by the sectoral balances.

Refreshing the balances (again) – we know that from an accounting sense, if the external sector overall is in deficit, then it is impossible for both the private domestic sector and government sector to run surpluses. One of those two has to also be in deficit to satisfy the accounting rules.

The important point is to understand what behaviour and economic adjustments drive these outcomes.

To refresh your memory the sectoral balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.

We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all taxes and transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).

Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).

Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):

(2) GNP = C + I + G + (X – M) + FNI

To render this approach into the sectoral balances form, we subtract total taxes and transfers (T) from both sides of Expression (3) to get:

(3) GNP – T = C + I + G + (X – M) + FNI – T

Now we can collect the terms by arranging them according to the three sectoral balances:

(4) (GNP – C – T) – I = (G – T) + (X – M + FNI)

The the terms in Expression (4) are relatively easy to understand now.

The term (GNP – C – T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.

The left-hand side of Equation (4), (GNP – C – T) – I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP – C – T).

In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.

The term (G – T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.

Finally, the other right-hand side term (X – M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.

In English we could say that:

The private financial balance equals the sum of the government financial balance plus the current account balance.

We can re-write Expression (6) in this way to get the sectoral balances equation:

(5) (S – I) = (G – T) + CAD

which is interpreted as meaning that government sector deficits (G – T > 0) and current account surpluses (CAD > 0) generate national income and net financial assets for the private domestic sector.

Conversely, government surpluses (G – T < 0) and current account deficits (CAD < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets.

Expression (5) can also be written as:

(6) [(S – I) – CAD] = (G – T)

where the term on the left-hand side [(S – I) – CAD] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance.

This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit).

The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers.

All these relationships (equations) hold as a matter of accounting and not matters of opinion.

So what economic behaviour might lead to the outcome specified in the question?

If the nation is running an external deficit it means that the contribution to aggregate demand from the external sector is negative – that is net drain of spending – dragging output down.

Assume, now that the private domestic sector (households and firms) seeks to increase its saving ratio (as a percentage of GDP). Consistent with this aspiration, households may cut back on consumption spending and save more out of disposable income. The immediate impact is that aggregate demand will fall and inventories will start to increase beyond the desired level of the firms.

The firms will soon react to the increased inventory holding costs and will start to cut back production. How quickly this happens depends on a number of factors including the pace and magnitude of the initial demand contraction. But if the households persist in trying to save more and consumption continues to lag, then soon enough the economy starts to contract – output, employment and income all fall.

The initial contraction in consumption multiplies through the expenditure system as workers who are laid off also lose income and their spending declines. This leads to further contractions.

The declining income leads to a number of consequences. Net exports improve as imports fall (less income) but the question clearly assumes that the external sector remains in deficit. Total saving actually starts to decline as income falls as does induced consumption.

So the initial discretionary decline in consumption is supplemented by the induced consumption falls driven by the multiplier process.

The decline in income then stifles firms’ investment plans – they become pessimistic of the chances of realising the output derived from augmented capacity and so aggregate demand plunges further. Both these effects push the private domestic balance further towards and eventually into surplus

With the economy in decline, tax revenue falls and welfare payments rise which push the public fiscal balance towards and eventually into deficit via the automatic stabilisers.

If the private sector persists in trying to increase its saving ratio then the contracting income will clearly push the fiscal balance into deficit.

So we would have an external deficit, a private domestic surplus and a fiscal deficit.

The following blogs may be of further interest to you:

• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!

Question 3:

If the central bank pays a positive interest rate on overnight reserves then it no longer would have to conduct open market operations to ensure its policy rate is sustained (ignore any reserve requirements).

The answer is False.

The first question starts with a test of basic understandings of how monetary policy is implemented in a modern monetary economy. Contrary to the account of monetary policy in mainstream macroeconomics textbooks, which tries to tell students that monetary policy describes the processes by which the central bank determines “the total amount of money in existence or to alter that amount”.

In Mankiw’s Principles of Economics (Chapter 27 First Edition) he say that the central bank has “two related jobs”. The first is to “regulate the banks and ensure the health of the financial system” and the second “and more important job”:

… is to control the quantity of money that is made available to the economy, called the money supply. Decisions by policymakers concerning the money supply constitute monetary policy (emphasis in original).

How does the mainstream see the central bank accomplishing this task? Mankiw says:

Fed’s primary tool is open-market operations – the purchase and sale of U.S government bonds … If the FOMC decides to increase the money supply, the Fed creates dollars and uses them buy government bonds from the public in the nation’s bond markets. After the purchase, these dollars are in the hands of the public. Thus an open market purchase of bonds by the Fed increases the money supply. Conversely, if the FOMC decides to decrease the money supply, the Fed sells government bonds from its portfolio to the public in the nation’s bond markets. After the sale, the dollars it receives for the bonds are out of the hands of the public. Thus an open market sale of bonds by the Fed decreases the money supply.

This description of the way the central bank interacts with the banking system and the wider economy is totally false. The reality is that monetary policy is focused on determining the value of a short-term interest rate. Central banks cannot control the money supply. To some extent these ideas were a residual of the commodity money systems where the central bank could clearly control the stock of gold, for example. But in a credit money system, this ability to control the stock of “money” is undermined by the demand for credit.

The theory of endogenous money is central to the horizontal analysis in Modern Monetary Theory (MMT). When we talk about endogenous money we are referring to the outcomes that are arrived at after market participants respond to their own market prospects and central bank policy settings and make decisions about the liquid assets they will hold (deposits) and new liquid assets they will seek (loans).

The essential idea is that the “money supply” in an “entrepreneurial economy” is demand-determined – as the demand for credit expands so does the money supply.

As credit is repaid the money supply shrinks. These flows are going on all the time and the stock measure we choose to call the money supply, say M3 (Currency plus bank current deposits of the private non-bank sector plus all other bank deposits from the private non-bank sector) is just an arbitrary reflection of the credit circuit.

So the supply of money is determined endogenously by the level of GDP, which means it is a dynamic (rather than a static) concept.

Central banks clearly do not determine the volume of deposits held each day. These arise from decisions by commercial banks to make loans. The central bank can determine the price of “money” by setting the interest rate on bank reserves. Further expanding the monetary base (bank reserves) as we have argued in recent blogs – Building bank reserves will not expand credit and Building bank reserves is not inflationary – does not lead to an expansion of credit.

With this background in mind, the question is specifically about the dynamics of bank reserves which are used to satisfy any imposed reserve requirements and facilitate the payments system. These dynamics have a direct bearing on monetary policy settings. Given that the dynamics of the reserves can undermine the desired monetary policy stance (as summarised by the policy interest rate setting), the central banks have to engage in liquidity management operations.

What are these liquidity management operations?

Well you first need to appreciate what reserve balances are.

The New York Federal Reserve Bank’s paper – Divorcing Money from Monetary Policy said that:

… reserve balances are used to make interbank payments; thus, they serve as the final form of settlement for a vast array of transactions. The quantity of reserves needed for payment purposes typically far exceeds the quantity consistent with the central bank’s desired interest rate. As a result, central banks must perform a balancing act, drastically increasing the supply of reserves during the day for payment purposes through the provision of daylight reserves (also called daylight credit) and then shrinking the supply back at the end of the day to be consistent with the desired market interest rate.

So the central bank must ensure that all private cheques (that are funded) clear and other interbank transactions occur smoothly as part of its role of maintaining financial stability. But, equally, it must also maintain the bank reserves in aggregate at a level that is consistent with its target policy setting given the relationship between the two.

So operating factors link the level of reserves to the monetary policy setting under certain circumstances. These circumstances require that the return on “excess” reserves held by the banks is below the monetary policy target rate. In addition to setting a lending rate (discount rate), the central bank also sets a support rate which is paid on commercial bank reserves held by the central bank.

Many countries (such as Australia and Canada) maintain a default return on surplus reserve accounts (for example, the Reserve Bank of Australia pays a default return equal to 25 basis points less than the overnight rate on surplus Exchange Settlement accounts). Other countries like the US and Japan have historically offered a zero return on reserves which means persistent excess liquidity would drive the short-term interest rate to zero.

The support rate effectively becomes the interest-rate floor for the economy. If the short-run or operational target interest rate, which represents the current monetary policy stance, is set by the central bank between the discount and support rate. This effectively creates a corridor or a spread within which the short-term interest rates can fluctuate with liquidity variability. It is this spread that the central bank manages in its daily operations.

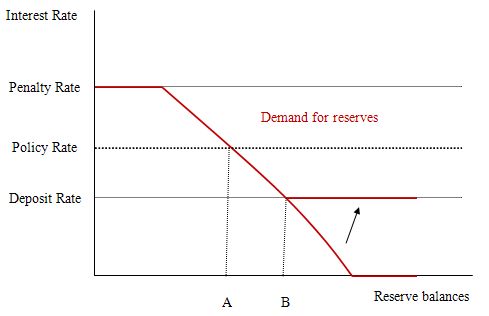
So the issue then becomes – at what level should the support rate be set? To answer that question, I reproduce a version of teh diagram from the FRBNY paper which outlined a simple model of the way in which reserves are manipulated by the central bank as part of its liquidity management operations designed to implement a specific monetary policy target (policy interest rate setting).

I describe the FRBNY model in detail in the blog – Understanding central bank operations so I won’t repeat that explanation.

The penalty rate is the rate the central bank charges for loans to banks to cover shortages of reserves. If the interbank rate is at the penalty rate then the banks will be indifferent as to where they access reserves from so the demand curve is horizontal (shown in red).

Once the price of reserves falls below the penalty rate, banks will then demand reserves according to their requirments (the legal and the perceived). The higher the market rate of interest, the higher is the opportunity cost of holding reserves and hence the lower will be the demand. As rates fall, the opportunity costs fall and the demand for reserves increases. But in all cases, banks will only seek to hold (in aggregate) the levels consistent with their requirements.

At low interest rates (say zero) banks will hold the legally-required reserves plus a buffer that ensures there is no risk of falling short during the operation of the payments system.

Commercial banks choose to hold reserves to ensure they can meet all their obligations with respect to the clearing house (payments) system. Because there is considerable uncertainty (for example, late-day payment flows after the interbank market has closed), a bank may find itself short of reserves. Depending on the circumstances, it may choose to keep a buffer stock of reserves just to meet these contingencies.

So central bank reserves are intrinsic to the payments system where a mass of interbank claims are resolved by manipulating the reserve balances that the banks hold at the central bank. This process has some expectational regularity on a day-to-day basis but stochastic (uncertain) demands for payments also occur which means that banks will hold surplus reserves to avoid paying any penalty arising from having reserve deficiencies at the end of the day (or accounting period).

To understand what is going on not that the diagram is representing the system-wide demand for bank reserves where the horizontal axis measures the total quantity of reserve balances held by banks while the vertical axis measures the market interest rate for overnight loans of these balances

In this diagram there are no required reserves (to simplify matters). We also initially, abstract from the deposit rate for the time being to understand what role it plays if we introduce it.

Without the deposit rate, the central bank has to ensure that it supplies enough reserves to meet demand while still maintaining its policy rate (the monetary policy setting.

So the model can demonstrate that the market rate of interest will be determined by the central bank supply of reserves. So the level of reserves supplied by the central bank supply brings the market rate of interest into line with the policy target rate.

At the supply level shown as Point A, the central bank can hit its monetary policy target rate of interest given the banks’ demand for aggregate reserves. So the central bank announces its target rate then undertakes monetary operations (liquidity management operations) to set the supply of reserves to this target level.

So contrary to what Mankiw’s textbook tells students the reality is that monetary policy is about changing the supply of reserves in such a way that the market rate is equal to the policy rate.

The central bank uses open market operations to manipulate the reserve level and so must be buying and selling government debt to add or drain reserves from the banking system in line with its policy target.

If there are excess reserves in the system and the central bank didn’t intervene then the market rate would drop towards zero and the central bank would lose control over its target rate (that is, monetary policy would be compromised).

As explained in the blog – Understanding central bank operations – the introduction of a support rate payment (deposit rate) whereby the central bank pays the member banks a return on reserves held overnight changes things considerably.

It clearly can – under certain circumstances – eliminate the need for any open-market operations to manage the volume of bank reserves.

In terms of the diagram, the major impact of the deposit rate is to lift the rate at which the demand curve becomes horizontal (as depicted by the new horizontal red segment moving up via the arrow).

This policy change allows the banks to earn overnight interest on their excess reserve holdings and becomes the minimum market interest rate and defines the lower bound of the corridor within which the market rate can fluctuate without central bank intervention.

So in this diagram, the market interest rate is still set by the supply of reserves (given the demand for reserves) and so the central bank still has to manage reserves appropriately to ensure it can hit its policy target.
If there are excess reserves in the system in this case, and the central bank didn’t intervene, then the market rate will drop to the support rate (at Point B).

So if the central bank wants to maintain control over its target rate it can either set a support rate below the desired policy rate (as in Australia) and then use open market operations to ensure the reserve supply is consistent with Point A or set the support (deposit) rate equal to the target policy rate.

The answer to the question is thus False because it all depends on where the support rate is set. Only if it set equal to the policy rate will there be no need for the central bank to manage liquidity via open market operations.

The following blogs may be of further interest to you:

• Understanding central bank operations
• Building bank reserves will not expand credit
• Building bank reserves is not inflationary

That is enough for today!

(c) Copyright 2017 William Mitchell. All Rights Reserved.