The Weekend Quiz – August 6-7, 2016 – answers and discussion

Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

If the national accounts of a nation reveal that its external surplus is equivalent to 2 per cent of GDP and the private domestic sector is saving overall 3 per cent of GDP then we would also observe:

(a) A fiscal deficit equal to 1 per cent of GDP.

(b) A fiscal surplus equal to 1 per cent of GDP.

(c) A fiscal deficit equal to 5 per cent of GDP.

(d) A fiscal surplus equal to 5 per cent of GDP.

The answer is Option (a) – A fiscal deficit equal to 1 per cent of GDP.

This question requires an understanding of the sectoral balances that can be derived from the National Accounts. But it also requires some understanding of the behavioural relationships within and between these sectors which generate the outcomes that are captured in the National Accounts and summarised by the sectoral balances.

Refreshing the balances (again) – we know that from an accounting sense, if the external sector overall is in deficit, then it is impossible for both the private domestic sector and government sector to run surpluses. One of those two has to also be in deficit to satisfy the accounting rules.

The important point is to understand what behaviour and economic adjustments drive these outcomes.

To refresh your memory the sectoral balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.

We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all taxes and transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).

Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).

Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):

(2) GNP = C + I + G + (X – M) + FNI

To render this approach into the sectoral balances form, we subtract total taxes and transfers (T) from both sides of Expression (3) to get:

(3) GNP – T = C + I + G + (X – M) + FNI – T

Now we can collect the terms by arranging them according to the three sectoral balances:

(4) (GNP – C – T) – I = (G – T) + (X – M + FNI)

The the terms in Expression (4) are relatively easy to understand now.

The term (GNP – C – T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.

The left-hand side of Equation (4), (GNP – C – T) – I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP – C – T).

In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.

The term (G – T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.

Finally, the other right-hand side term (X – M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.

In English we could say that:

The private financial balance equals the sum of the government financial balance plus the current account balance.

We can re-write Expression (6) in this way to get the sectoral balances equation:

(5) (S – I) = (G – T) + CAD

which is interpreted as meaning that government sector deficits (G – T > 0) and current account surpluses (CAD > 0) generate national income and net financial assets for the private domestic sector.

Conversely, government surpluses (G – T < 0) and current account deficits (CAD < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets. Expression (5) can also be written as: (6) [(S - I) - CAD] = (G - T) where the term on the left-hand side [(S - I) - CAD] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance. This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit). The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers. All these relationships (equations) hold as a matter of accounting and not matters of opinion. So what economic behaviour might lead to the outcome specified in the question? 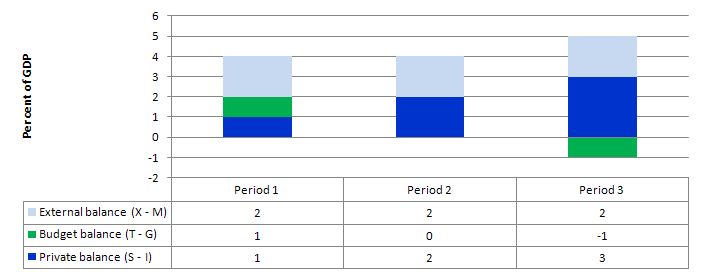The following graph shows three situations where the external sector is in surplus of 2 per cent of GDP and the private domestic balance is in surplus of varying proportions of GDP (note I have written the fiscal balance as (T - G). In Period 1, the private domestic balance is in surplus (1 per cent of GDP), which means it is saving overall (spending less than the total private income) and the fiscal outcome is also in surplus (1 per cent of GDP). The net injection to demand from the external sector (equivalent to 2 per cent of GDP) is sufficient to "fund" the overall private sector saving drain from expenditure without compromising economic growth. The growth in income would also allow the fiscal outcome to be in surplus (via tax revenue). In Period 2, the rise in overall private domestic saving drains extra aggregate demand and necessitates a more expansionary position from the government (relative to Period 1), which in this case manifests as a balanced public fiscal position. Period 3, relates to the data presented in the question - an external surplus of 2 per cent of GDP and private domestic saving equal to 3 per cent of GDP. Now the demand injection from the external sector is being more than offset by the demand drain from private domestic saving. The income adjustments that would occur in this economy would then push the fiscal outcome into deficit of 1 per cent of GDP. The movements in income associated with the spending and revenue patterns will ensure these balances arise. The general rule is that the government fiscal deficit (surplus) will always equal the non-government surplus (deficit). So if there is an external surplus that is less than the overall private domestic sector saving (a surplus) then there will always be a fiscal deficit. The higher the overall private saving is relative to the external surplus, the larger the deficit.

The following blogs may be of further interest to you:

• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!

Question 2:

The British government’s fiscal deficit rose despite the Conservative government’s stated fiscal austerity stance. We can conclude from that fact that the austerity mantra of the British government doesn’t correctly describe its fiscal policy stance.

The answer is False.

The actual fiscal deficit outcome that is reported in the press and by Treasury departments is not a pure measure of the discretionary fiscal policy stance adopted by the government at any point in time. As a result, a straightforward interpretation of

Economists conceptualise the actual fiscal outcome as being the sum of two components: (a) a discretionary component – that is, the actual fiscal stance intended by the government; and (b) a cyclical component reflecting the sensitivity of certain fiscal items (tax revenue based on activity and welfare payments to name the most sensitive) to changes in the level of activity.

The former component is now called the “structural deficit” and the latter component is sometimes referred to as the automatic stabilisers.

The structural deficit thus conceptually reflects the chosen (discretionary) fiscal stance of the government independent of cyclical factors.

The cyclical factors refer to the automatic stabilisers which operate in a counter-cyclical fashion. When economic growth is strong, tax revenue improves given it is typically tied to income generation in some way. Further, most governments provide transfer payment relief to workers (unemployment benefits) and this decreases during growth.

In times of economic decline, the automatic stabilisers work in the opposite direction and push the fiscal balance towards deficit, into deficit, or into a larger deficit. These automatic movements in aggregate demand play an important counter-cyclical attenuating role. So when GDP is declining due to falling aggregate demand, the automatic stabilisers work to add demand (falling taxes and rising welfare payments). When GDP growth is rising, the automatic stabilisers start to pull demand back as the economy adjusts (rising taxes and falling welfare payments).

The problem is then how to determine whether the chosen discretionary fiscal stance is adding to demand (expansionary) or reducing demand (contractionary). It is a problem because a government could be run a contractionary policy by choice but the automatic stabilisers are so strong that the fiscal outcome goes into deficit which might lead people to think the “government” is expanding the economy.

So just because the fiscal outcome goes into deficit doesn’t allow us to conclude that the Government has suddenly become of an expansionary mind. In other words, the presence of automatic stabilisers make it hard to discern whether the fiscal policy stance (chosen by the government) is contractionary or expansionary at any particular point in time.

To overcome this ambiguity, economists decided to measure the automatic stabiliser impact against some benchmark or “full capacity” or potential level of output, so that we can decompose the fiscal balance into that component which is due to specific discretionary fiscal policy choices made by the government and that which arises because the cycle takes the economy away from the potential level of output.

As a result, economists devised what used to be called the Full Employment or High Employment Budget. In more recent times, this concept is now called the Structural Balance.

The Full Employment Budget Balance was a hypothetical construction of the fiscal balance that would be realised if the economy was operating at potential or full employment. In other words, calibrating the fiscal position (and the underlying fiscal parameters) against some fixed point (full capacity) eliminated the cyclical component – the swings in activity around full employment.

This framework allowed economists to decompose the actual fiscal balance into (in modern terminology) the structural (discretionary) and cyclical fiscal balances with these unseen fiscal components being adjusted to what they would be at the potential or full capacity level of output.

The difference between the actual fiscal outcome and the structural component is then considered to be the cyclical fiscal outcome and it arises because the economy is deviating from its potential.

So if the economy is operating below capacity then tax revenue would be below its potential level and welfare spending would be above. In other words, the fiscal balance would be smaller at potential output relative to its current value if the economy was operating below full capacity. The adjustments would work in reverse should the economy be operating above full capacity.

If the fiscal outcome is in deficit when computed at the “full employment” or potential output level, then we call this a structural deficit and it means that the overall impact of discretionary fiscal policy is expansionary irrespective of what the actual fiscal outcome is presently. If it is in surplus, then we have a structural surplus and it means that the overall impact of discretionary fiscal policy is contractionary irrespective of what the actual fiscal outcome is presently.

So you could have a downturn which drives the fiscal outcome into a deficit but the underlying structural position could be contractionary (that is, a surplus). And vice versa.

The question then relates to how the “potential” or benchmark level of output is to be measured. The calculation of the structural deficit spawned a bit of an industry among the profession raising lots of complex issues relating to adjustments for inflation, terms of trade effects, changes in interest rates and more.

Much of the debate centred on how to compute the unobserved full employment point in the economy. There were a plethora of methods used in the period of true full employment in the 1960s.

As the neo-liberal resurgence gained traction in the 1970s and beyond and governments abandoned their commitment to full employment , the concept of the Non-Accelerating Inflation Rate of Unemployment (the NAIRU) entered the debate – see my blogs – The dreaded NAIRU is still about and Redefing full employment … again!.

The NAIRU became a central plank in the front-line attack on the use of discretionary fiscal policy by governments. It was argued, erroneously, that full employment did not mean the state where there were enough jobs to satisfy the preferences of the available workforce. Instead full employment occurred when the unemployment rate was at the level where inflation was stable.

The estimated NAIRU (it is not observed) became the standard measure of full capacity utilisation. If the economy is running an unemployment equal to the estimated NAIRU then mainstream economists concluded that the economy is at full capacity. Of-course, they kept changing their estimates of the NAIRU which were in turn accompanied by huge standard errors. These error bands in the estimates meant their calculated NAIRUs might vary between 3 and 13 per cent in some studies which made the concept useless for policy purposes.

Typically, the NAIRU estimates are much higher than any acceptable level of full employment and therefore full capacity. The change of the the name from Full Employment Budget Balance to Structural Balance was to avoid the connotations of the past where full capacity arose when there were enough jobs for all those who wanted to work at the current wage levels.

Now you will only read about structural balances which are benchmarked using the NAIRU or some derivation of it – which is, in turn, estimated using very spurious models. This allows them to compute the tax and spending that would occur at this so-called full employment point. But it severely underestimates the tax revenue and overestimates the spending because typically the estimated NAIRU always exceeds a reasonable (non-neo-liberal) definition of full employment.

So the estimates of structural deficits provided by all the international agencies and treasuries etc all conclude that the structural balance is more in deficit (less in surplus) than it actually is – that is, bias the representation of fiscal expansion upwards.

As a result, they systematically understate the degree of discretionary contraction coming from fiscal policy.

The only qualification is if the NAIRU measurement actually represented full employment. Then this source of bias would disappear.

So in terms of the question, a rising fiscal deficit can accompany a contractionary fiscal position if the cuts in the discretionary net spending leads to a decline in economic growth and the automatic stabilisers then drive the cyclical component higher and more than offset the discretionary component.

Without delving further into the actual factors that are delivering the fiscal outcome in Britain one cannot make the conclusion implied in the question.

The following blogs may be of further interest to you:

• A modern monetary theory lullaby
• Saturday Quiz – April 24, 2010 – answers and discussion
• The dreaded NAIRU is still about!
• Structural deficits – the great con job!
• Structural deficits and automatic stabilisers
• Another economics department to close

Question 3

In Year 1, the economy plunges into recession with nominal GDP growth falling to minus 1 per cent. The inflation rate is subdued at 2 per cent per annum. The outstanding public debt to GDP ratio was 100 per cent at the start of the year and the nominal interest rate remains at 2 per cent (and this is the rate the government pays on all outstanding debt). The government’s fiscal balance net of interest payments goes into deficit during the year equivalent to 1 per cent of GDP and the public debt ratio rises by 4 per cent. In Year 2, the government stimulates the economy and pushes the primary fiscal deficit out to 4 per cent of GDP in recognition of the severity of the recession. In doing so it stimulates aggregate demand and the economy records a 4 per cent nominal GDP growth rate. The central bank holds the nominal interest rate constant but inflation falls to 1 per cent given the slack nature of the economy the previous year. Under these circumstances, the public debt ratio falls in Year 2, even though the fiscal deficit has risen because of the real growth in the economy.

The answer is False.

This question requires you to understand the key parameters and relationships that determine the dynamics of the public debt ratio. An understanding of these relationships allows you to debunk statements that are made by those who think fiscal austerity will allow a government to reduce its public debt ratio.

While Modern Monetary Theory (MMT) places no particular importance in the public debt to GDP ratio for a sovereign government, given that insolvency is not an issue, the mainstream debate is dominated by the concept.

The unnecessary practice of fiat currency-issuing governments of issuing public debt $-for-$ to match public net spending (deficits) ensures that the debt levels will rise when there are deficits.

Rising deficits usually mean declining economic activity (especially if there is no evidence of accelerating inflation) which suggests that the debt/GDP ratio may be rising because the denominator is also likely to be falling or rising below trend.

Further, historical experience tells us that when economic growth resumes after a major recession, during which the public debt ratio can rise sharply, the latter always declines again.

It is this endogenous nature of the ratio that suggests it is far more important to focus on the underlying economic problems which the public debt ratio just mirrors.

Mainstream economics starts with the flawed analogy between the household and the sovereign government such that any excess in government spending over taxation receipts has to be “financed” in two ways: (a) by borrowing from the public; and/or (b) by “printing money”.

Neither characterisation is remotely representative of what happens in the real world in terms of the operations that define transactions between the government and non-government sector.

Further, the basic analogy is flawed at its most elemental level. The household must work out the financing before it can spend. The household cannot spend first. The government can spend first and ultimately does not have to worry about financing such expenditure.

However, the mainstream framework for analysing these so-called “financing” choices is called the government budget constraint (GBC). The GBC says that the fiscal deficit in year t is equal to the change in government debt over year t plus the change in high powered money over year t. So in mathematical terms it is written as:

which you can read in English as saying that Budget deficit = Government spending + Government interest payments – Tax receipts must equal (be “financed” by) a change in Bonds (B) and/or a change in high powered money (H). The triangle sign (delta) is just shorthand for the change in a variable.

However, this is merely an accounting statement. In a stock-flow consistent macroeconomics, this statement will always hold. That is, it has to be true if all the transactions between the government and non-government sector have been corrected added and subtracted.

So in terms of MMT, the previous equation is just an ex post accounting identity that has to be true by definition and has not real economic importance.

But for the mainstream economist, the equation represents an ex ante (before the fact) financial constraint that the government is bound by. The difference between these two conceptions is very significant and the second (mainstream) interpretation cannot be correct if governments issue fiat currency (unless they place voluntary constraints on themselves to act as if it is).

Further, in mainstream economics, money creation is erroneously depicted as the government asking the central bank to buy treasury bonds which the central bank in return then prints money. The government then spends this money.

This is called debt monetisation and you can find out why this is typically not a viable option for a central bank by reading the Deficits 101 suite – Deficit spending 101 – Part 1 – Deficit spending 101 – Part 2 – Deficit spending 101 – Part 3.

The mainstream view claims that if governments increase the money growth rate (they erroneously call this “printing money”) the extra spending will cause accelerating inflation because there will be “too much money chasing too few goods”! Of-course, we know that proposition to be generally preposterous because economies that are constrained by deficient demand (defined as demand below the full employment level) respond to nominal demand increases by expanding real output rather than prices. There is an extensive literature pointing to this result.

So when governments are expanding deficits to offset a collapse in private spending, there is plenty of spare capacity available to ensure output rather than inflation increases.

But not to be daunted by the “facts”, the mainstream claim that because inflation is inevitable if “printing money” occurs, it is unwise to use this option to “finance” net public spending.

Hence they say as a better (but still poor) solution, governments should use debt issuance to “finance” their deficits. Thy also claim this is a poor option because in the short-term it is alleged to increase interest rates and in the longer-term is results in higher future tax rates because the debt has to be “paid back”.

Neither proposition bears scrutiny – you can read these blogs – Will we really pay higher taxes? and Will we really pay higher interest rates? – for further discussion on these points.

The mainstream textbooks are full of elaborate models of debt pay-back, debt stabilisation etc which all claim (falsely) to “prove” that the legacy of past deficits is higher debt and to stabilise the debt, the government must eliminate the deficit which means it must then run a primary surplus equal to interest payments on the existing debt.

A primary fiscal balance is the difference between government spending (excluding interest rate servicing) and taxation revenue.

The standard mainstream framework, which even the so-called progressives (deficit-doves) use, focuses on the ratio of debt to GDP rather than the level of debt per se. The following equation captures the approach:

So the change in the debt ratio is the sum of two terms on the right-hand side: (a) the difference between the real interest rate (r) and the real GDP growth rate (g) times the initial debt ratio; and (b) the ratio of the primary deficit (G-T) to GDP.

The real interest rate is the difference between the nominal interest rate and the inflation rate. Real GDP is the nominal GDP deflated by the inflation rate. So the real GDP growth rate is equal to the Nominal GDP growth minus the inflation rate.

This standard mainstream framework is used to highlight the dangers of running deficits. But even progressives (not me) use it in a perverse way to justify deficits in a downturn balanced by surpluses in the upturn.

MMT does not tell us that a currency-issuing government running a deficit can never reduce the debt ratio. The standard formula above can easily demonstrate that a nation running a primary deficit can reduce its public debt ratio over time.

Furthermore, depending on contributions from the external sector, a nation running a deficit will more likely create the conditions for a reduction in the public debt ratio than a nation that introduces an austerity plan aimed at running primary surpluses.

But if growth is not sufficient then the public debt ratio can rise.

Here is why that is the case.

While a growing economy can absorb more debt and keep the debt ratio constant or falling an increasing real interest rate also means that interest payments on the outstanding stock of debt rise.

From the formula above, if the primary fiscal balance is zero, public debt increases at a rate r but the public debt ratio increases at r – g.

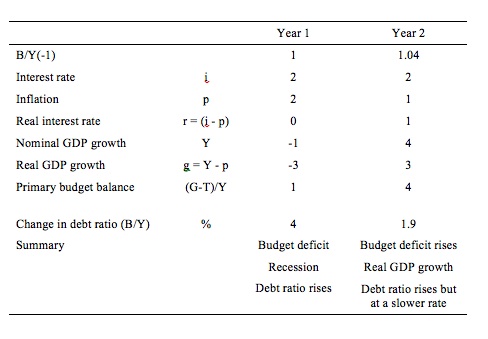
The following Table simulates the two years in question. To make matters simple, assume a public debt ratio at the start of the Year 1 of 100 per cent (so B/Y(-1) = 1) which is equivalent to the statement that “outstanding public debt is equal to the value of the nominal GDP”.

In Year 1, the nominal interest rate is 2 per cent and the inflation rate is 2 per cent then the current real interest rate (r) is 0 per cent.

If the nominal GDP grows at -1 per cent and there is an inflation rate of 2 per cent then real GDP is growing (g) at minus 3 per cent.

Under these conditions, the primary fiscal surplus would have to be equal to 3 per cent of GDP to stabilise the debt ratio (check it for yourself).

In Year 1, the primary fiscal deficit is actually 1 per cent of GDP so we know by computation that the public debt ratio rises by 4 per cent.

The calculation (using the formula in the Table) is:

Change in B/Y = (0 – (-3))*1 + 1 = 4 per cent.

The situation gets more complex in Year 2 because the inflation rate falls to 1 per cent while the central bank holds the nominal interest rate constant at 2 per cent. So the real interest rate rises to 1 per cent.

The data in Year 2 is given in the last column in the Table below. Note the public debt ratio at the beginning of the period has risen to 1.04 because of the rise from last year.

You are told that the fiscal deficit rises to 4 per cent of GDP and nominal GDP growth shoots up to 4 per cent which means real GDP growth (given the inflation rate) is equal to 3 per cent.

The corresponding calculation for the change in the public debt ratio is:

Change in B/Y = (1 – 3)*1.04 + 5 = 1.9 per cent.

That is, the public debt ratio rises but at a slower rate than in the last year. The real growth in the economy has been beneficial and if maintained would start to eat into the primary fiscal balance (via the rising tax revenues that would occur).

In a few years, the growth would not only reduce the primary fiscal deficit but the public debt ratio would start to decline as well.

So when the fiscal deficit is a large percentage of GDP then it might take some years to start reducing the public debt ratio as GDP growth ensures.

The best way to reduce the public debt ratio is to stop issuing debt. A sovereign government doesn’t have to issue debt if the central bank is happy to keep its target interest rate at zero or pay interest on excess reserves.

The discussion also demonstrates why a falling inflation rate makes it harder for the government to reduce the public debt ratio – which, of-course, is one of the more subtle mainstream ways to force the government to run surpluses.