Saturday Quiz – October 23, 2010 – answers and discussion

Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

A budget deficit equivalent to 3 per cent of GDP signals that the government is adopting a less expansionary policy than if the budget deficit outcome was equivalent to 5 per cent of GDP.

The answer is Maybe.

The question probes an understanding of the forces (components) that drive the budget balance that is reported by government agencies at various points in time.

In outright terms, a budget deficit that is equivalent to 5 per cent of GDP is more expansionary than a budget deficit outcome that is equivalent to 3 per cent of GDP. But that is not what the question asked. The question asked whether that signalled that the government is adopting a less expansionary policy – that is, whether its discretionary fiscal intent was expansionary.

In other words, what does the budget outcome signal about the discretionary fiscal stance adopted by the government.

To see the difference between these statements we have to explore the issue of decomposing the observed budget balance into the discretionary (now called structural) and cyclical components. The latter component is driven by the automatic stabilisers that are in-built into the budget process.

The federal (or national) government budget balance is the difference between total federal revenue and total federal outlays. So if total revenue is greater than outlays, the budget is in surplus and vice versa. It is a simple matter of accounting with no theory involved. However, the budget balance is used by all and sundry to indicate the fiscal stance of the government.

So if the budget is in surplus it is often concluded that the fiscal impact of government is contractionary (withdrawing net spending) and if the budget is in deficit we say the fiscal impact expansionary (adding net spending).

Further, a rising deficit (falling surplus) is often considered to be reflecting an expansionary policy stance and vice versa. What we know is that a rising deficit may, in fact, indicate a contractionary fiscal stance – which, in turn, creates such income losses that the automatic stabilisers start driving the budget back towards (or into) deficit.

So the complication is that we cannot conclude that changes in the fiscal impact reflect discretionary policy changes. The reason for this uncertainty clearly relates to the operation of the automatic stabilisers.

To see this, the most simple model of the budget balance we might think of can be written as:

Budget Balance = Revenue – Spending.

Budget Balance = (Tax Revenue + Other Revenue) – (Welfare Payments + Other Spending)

We know that Tax Revenue and Welfare Payments move inversely with respect to each other, with the latter rising when GDP growth falls and the former rises with GDP growth. These components of the budget balance are the so-called automatic stabilisers.

In other words, without any discretionary policy changes, the budget balance will vary over the course of the business cycle. When the economy is weak – tax revenue falls and welfare payments rise and so the budget balance moves towards deficit (or an increasing deficit). When the economy is stronger – tax revenue rises and welfare payments fall and the budget balance becomes increasingly positive. Automatic stabilisers attenuate the amplitude in the business cycle by expanding the budget in a recession and contracting it in a boom.

So just because the budget goes into deficit or the deficit increases as a proportion of GDP doesn’t allow us to conclude that the Government has suddenly become of an expansionary mind. In other words, the presence of automatic stabilisers make it hard to discern whether the fiscal policy stance (chosen by the government) is contractionary or expansionary at any particular point in time.

To overcome this uncertainty, economists devised what used to be called the Full Employment or High Employment Budget. In more recent times, this concept is now called the Structural Balance. The Full Employment Budget Balance was a hypothetical construct of the budget balance that would be realised if the economy was operating at potential or full employment. In other words, calibrating the budget position (and the underlying budget parameters) against some fixed point (full capacity) eliminated the cyclical component – the swings in activity around full employment.

So a full employment budget would be balanced if total outlays and total revenue were equal when the economy was operating at total capacity. If the budget was in surplus at full capacity, then we would conclude that the discretionary structure of the budget was contractionary and vice versa if the budget was in deficit at full capacity.

The calculation of the structural deficit spawned a bit of an industry in the past with lots of complex issues relating to adjustments for inflation, terms of trade effects, changes in interest rates and more.

Much of the debate centred on how to compute the unobserved full employment point in the economy. There were a plethora of methods used in the period of true full employment in the 1960s. All of them had issues but like all empirical work – it was a dirty science – relying on assumptions and simplifications. But that is the nature of the applied economist’s life.

As I explain in the blogs cited below, the measurement issues have a long history and current techniques and frameworks based on the concept of the Non-
Accelerating Inflation Rate of Unemployment (the NAIRU) bias the resulting analysis such that actual discretionary positions which are contractionary are seen as being less so and expansionary positions are seen as being more expansionary.

The result is that modern depictions of the structural deficit systematically understate the degree of discretionary contraction coming from fiscal policy.

So the data provided by the question could indicate a more expansionary fiscal intent from government but it could also indicate a large automatic stabiliser (cyclical) component.

Therefore the best answer is Maybe because there are circumstances where the proposition will not hold. It doesn’t always hold.

You might like to read these blogs for further information:

• Structural deficits and automatic stabilisers
• Structural deficits – the great con job!

Question 2:

When the government borrows from the private sector to match an increase in net public spending, the resulting increase in aggregate demand is less than would be the case if there was no bond sale.

The answer is false.

The mainstream macroeconomic textbooks all have a chapter on fiscal policy (and it is often written in the context of the so-called IS-LM model but not always).

The chapters always introduces the so-called Government Budget Constraint that alleges that governments have to “finance” all spending either through taxation; debt-issuance; or money creation. The writer fails to understand that government spending is performed in the same way irrespective of the accompanying monetary operations.

The textbook argument claims that money creation (borrowing from central bank) is inflationary while the latter (private bond sales) is less so. These conclusions are based on their erroneous claim that “money creation” adds more to aggregate demand than bond sales, because the latter forces up interest rates which crowd out some private spending.

All these claims are without foundation in a fiat monetary system and an understanding of the banking operations that occur when governments spend and issue debt helps to show why.

So what would happen if a sovereign, currency-issuing government (with a flexible exchange rate) ran a budget deficit without issuing debt?

Like all government spending, the Treasury would credit the reserve accounts held by the commercial bank at the central bank. The commercial bank in question would be where the target of the spending had an account. So the commercial bank’s assets rise and its liabilities also increase because a deposit would be made.

The transactions are clear: The commercial bank’s assets rise and its liabilities also increase because a new deposit has been made.

Further, the target of the fiscal initiative enjoys increased assets (bank deposit) and net worth (a liability/equity entry on their balance sheet).

Taxation does the opposite and so a deficit (spending greater than taxation) means that reserves increase and private net worth increases.

This means that there are likely to be excess reserves in the “cash system” which then raises issues for the central bank about its liquidity management. The aim of the central bank is to “hit” a target interest rate and so it has to ensure that competitive forces in the interbank market do not compromise that target.

When there are excess reserves there is downward pressure on the overnight interest rate (as banks scurry to seek interest-earning opportunities), the central bank then has to sell government bonds to the banks to soak the excess up and maintain liquidity at a level consistent with the target.

Some central banks offer a return on overnight reserves which reduces the need to sell debt as a liquidity management operation.

There is no sense that these debt sales have anything to do with “financing” government net spending. The sales are a monetary operation aimed at interest-rate maintenance.

So M1 (deposits in the non-government sector) rise as a result of the deficit without a corresponding increase in liabilities. It is this result that leads to the conclusion that that deficits increase net financial assets in the non-government sector.

What would happen if there were bond sales? All that happens is that the banks reserves are reduced by the bond sales but this does not reduce the deposits created by the net spending. So net worth is not altered. What is changed is the composition of the asset portfolio held in the non-government sector.

The only difference between the Treasury “borrowing from the central bank” and issuing debt to the private sector is that the central bank has to use different operations to pursue its policy interest rate target. If it debt is not issued to match the deficit then it has to either pay interest on excess reserves (which most central banks are doing now anyway) or let the target rate fall to zero (the Japan solution).

There is no difference to the impact of the deficits on net worth in the non-government sector.

Mainstream economists would say that by draining the reserves, the central bank has reduced the ability of banks to lend which then, via the money multiplier, expands the money supply.

However, the reality is that:

• Building bank reserves does not increase the ability of the banks to lend.
• The money multiplier process so loved by the mainstream does not describe the way in which banks make loans.
• Inflation is caused by aggregate demand growing faster than real output capacity. The reserve position of the banks is not functionally related with that process.

So the banks are able to create as much credit as they can find credit-worthy customers to hold irrespective of the operations that accompany government net spending.

This doesn’t lead to the conclusion that deficits do not carry an inflation risk. All components of aggregate demand carry an inflation risk if they become excessive, which can only be defined in terms of the relation between spending and productive capacity.

It is totally fallacious to think that private placement of debt reduces the inflation risk. It does not.

You may wish to read the following blogs for more information:

• Why history matters
• Building bank reserves will not expand credit
• Building bank reserves is not inflationary
• The complacent students sit and listen to some of that

Question 3:

If the external balance remains in surplus, then the national government will not impede economic growth by running a budget surplus.

The answer is false.

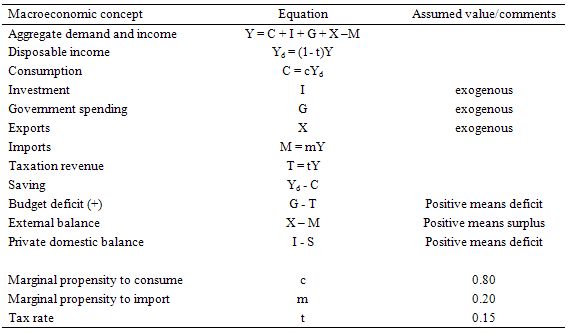
First, you need to understand the basic relationship between the sectoral flows and the balances that are derived from them. The flows are derived from the National Accounting relationship between aggregate spending and income. So:

(1) Y = C + I + G + (X – M)

where Y is GDP (income), C is consumption spending, I is investment spending, G is government spending, X is exports and M is imports (so X – M = net exports).

Another perspective on the national income accounting is to note that households can use total income (Y) for the following uses:

(2) Y = C + S + T

where S is total saving and T is total taxation (the other variables are as previously defined).

You than then bring the two perspectives together (because they are both just “views” of Y) to write:

(3) C + S + T = Y = C + I + G + (X – M)

You can then drop the C (common on both sides) and you get:

(4) S + T = I + G + (X – M)

Then you can convert this into the familiar sectoral balances accounting relations which allow us to understand the influence of fiscal policy over private sector indebtedness.

So we can re-arrange Equation (4) to get the accounting identity for the three sectoral balances – private domestic, government budget and external:

(S – I) = (G – T) + (X – M)

The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.

Another way of saying this is that total private savings (S) is equal to private investment (I) plus the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.

All these relationships (equations) hold as a matter of accounting and not matters of opinion.

Thus, when an external deficit (X – M < 0) and public surplus (G – T < 0) coincide, there must be a private deficit. While private spending can persist for a time under these conditions using the net savings of the external sector, the private sector becomes increasingly indebted in the process.

Second, you then have to appreciate the relative sizes of these balances to answer the question correctly.

Consider the following Table which depicts three cases – two that define a state of macroeconomic equilibrium (where aggregate demand equals income and firms have no incentive to change output) and one (Case 2) where the economy is in a disequilibrium state and income changes would occur.

Note that in the equilibrium cases, the (S – I) = (G – T) + (X – M) whereas in the disequilibrium case (S – I) > (G – T) + (X – M) meaning that aggregate demand is falling and a spending gap is opening up. Firms respond to that gap by decreasing output and income and this brings about an adjustment in the balances until they are back in equality.

So in Case 1, assume that the private domestic sector desires to save 2 per cent of GDP overall (spend less than they earn) and the external sector is running a surplus equal to 4 per cent of GDP.

In that case, aggregate demand will be unchanged if the government runs a surplus of 2 per cent of GDP (noting a negative sign on the government balance means T > G).

In this situation, the surplus does not undermine economic growth because the injections into the spending stream (NX) are exactly offset by the leakages in the form of the private saving and the budget surplus. This is the Norwegian situation.

In Case 2, we hypothesise that the private domestic sector now wants to save 6 per cent of GDP and they translate this intention into action by cutting back consumption (and perhaps investment) spending.

Clearly, aggregate demand now falls by 4 per cent of GDP and if the government tried to maintain that surplus of 2 per cent of GDP, the spending gap would start driving GDP downwards.

The falling income would not only reduce the capacity of the private sector to save but would also push the budget balance towards deficit via the automatic stabilisers. It would also push the external surplus up as imports fell. Eventually the income adjustments would restore the balances but with lower GDP overall.

So Case 2 is a not a position of rest – or steady growth. It is one where the government sector (for a given net exports position) is undermining the changing intentions of the private sector to increase their overall saving.

In Case 3, you see the result of the government sector accommodating that rising desire to save by the private sector by running a deficit of 2 per cent of GDP.

So the injections into the spending stream are 4 per cent from NX and 2 per cent from the deficit which exactly offset the desire of the private sector to save 6 per cent of GDP. At that point, the system would be in rest.

This is a highly stylised example and you could tell a myriad of stories that would be different in description but none that could alter the basic point.

If the drain on spending outweighs the injections into the spending stream then GDP falls (or growth is reduced).

So even though an external surplus is being run, the desired budget balance still depends on the saving desires of the private domestic sector. Under some situations, these desires could require a deficit even with an external surplus.

You may wish to read the following blogs for more information:

• Back to basics – aggregate demand drives output
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!
• Barnaby, better to walk before we run
• Saturday Quiz – June 19, 2010 – answers and discussion

Question 4:

Fiscal rules such as are embodied in the Stability and Growth Pact of the EMU will continually create conditions of slower growth because they deprive the government of fiscal flexibility to support aggregate demand when necessary.

The answer is False.

One word in the question renders this proposition false. I had originally worded the question (following EMU) “will bias the nations to slower growth” etc which is true and I considered that too easy.

The fiscal policy rules that were agreed in the Maastricht Treaty – budget deficits should not exceed 3 per cent of GDP and public debt should not exceed 60 per cent of GDP – clearly constrain EMU governments during periods when private spending (or net exports) are draining aggregate demand.

In those circumstances, if the private spending withdrawal is sufficiently severe, the automatic stabilisers alone will drive the budget deficit above the required limits. Pressure then is immediately placed on the national governments to introduce discretionary fiscal contractions to get the fiscal balance back within the limits.

Further, after an extended recession, the public debt ratios will almost always go beyond the allowable limits which places further pressure on the government to introduce an extended period of austerity to bring the ratio back within the limits. So the bias is towards slower growth overall.

It is also true that the fiscal rules clearly (and by design) “deprive the government of fiscal flexibility to support aggregate demand when necessary”. But that wasn’t the question. The question was will these rules continually create conditions of slower growth. The answer is no they will not.

Imagine a situation where the nation has very strong net exports adding to aggregate demand which supports steady growth and full employment without any need for the government to approach the Maastricht thresholds. In this case, the fiscal rules are never binding unless something happens to exports.

The following is an example of this sort of nation. It will take a while for you to work through but it provides a good learning environment for understanding the basic expenditure-income model upon with Modern Monetary Theory (MMT) builds its monetary insights. You might want to read this blog – Back to basics – aggregate demand drives output – to refresh your understanding of the sectoral balances.

The following Table shows the structure of the simple macroeconomic model that is the foundation of the expenditure-income model. This sort of model is still taught in introductory macroeconomics courses before the students get diverted into the more nonsensical mainstream ideas. All the assumptions with respect to behavioural parameters are very standard. You can download the simple spreadsheet if you want to play around with the model yourselves.

The first Table shows the model structure and any behavioural assumptions used. By way of explanation:

• All flows are in real terms with the price level constant (set at whatever you want it to be). So we are assuming that there is capacity within the supply-side of the economy to respond in real terms when nominal demand (which also equals real demand) changes.
• We might assume that the economy is at full employment in period 1 and in a state of excess capacity of varying degrees in each of the subsequent periods.
• Fiscal policy dominates monetary policy and the latter is assumed unchanged throughout. The central bank sets the interest rate and it doesn’t move.
• The tax rate is 0.15 throughout – so for every dollar of national income earned 15 cents is taken out in tax.
• The marginal propensity to consume is 0.8 – so for every dollar of disposable income 80 cents is consumed and 20 cents is saved.
• The marginal propensity to import is 0.2 – so for every dollar of national income (Y) 20 cents is lost from the expenditure stream into imports.

You might want to right-click the images to bring them up into a separate window and the print them (on recycled paper) to make it easier to follow the evolution of this economy over the 10 periods shown.

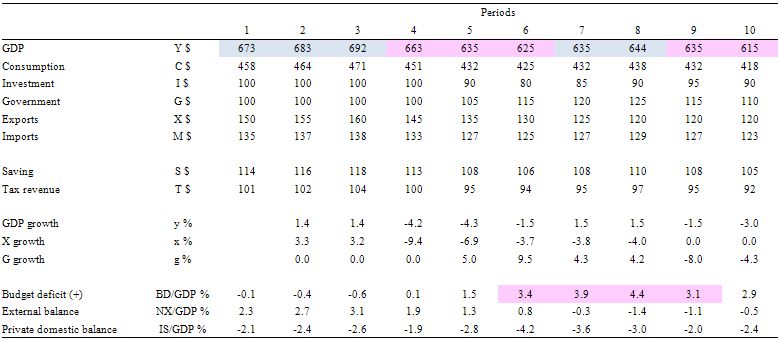
The next table quantifies the ten-period cycle and the graph below it presents the same information graphically for those who prefer pictures to numbers. The description of events is in between the table and the graph for those who do not want to print.

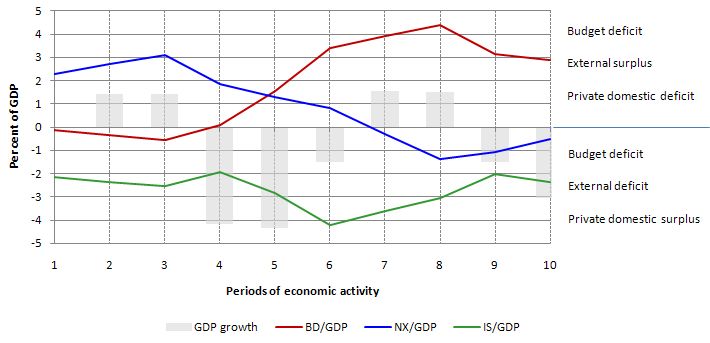
The graph below shows the sectoral balances – budget deficit (red line), external balance (blue line) and private domestic balance (green line) over the 10-period cycle as a percentage of GDP (Y) in addition to the period-by-period GDP growth (y) in percentage terms (grey bars).

Above the zero line means positive GDP growth, a budget deficit (G > T), an external surplus (X > M) and a private domestic deficit (I > S) and vice-versa for below the zero line.

This is an economy that is enjoying steady GDP growth (1.4 per cent) courtesy of a strong and growing export sector (surpluses in each of the first three periods). It is able to maintain strong growth via the export sector which permits a budget surplus (in each of the first three periods) and the private domestic sector is spending less than they are earning.

The budget parameters (and by implication the public debt ratio) is well within the Maastricht rules and not preventing strong (full employment growth) from occurring. You might say this is a downward bias but from in terms of an understanding of functional finance it just means that the government sector is achieving its goals (full employment) and presumably enough services and public infrastructure while being swamped with tax revenue as a result of the strong export sector.

Then in Period 4, there is a global recession and export markets deteriorate up and governments delay any fiscal stimulus. GDP growth plunges and the private domestic balance moves towards deficit. Total tax revenue falls and the budget deficit moves into balance all due to the automatic stabilisers. There has been no discretionary change in fiscal policy.

In Period 5, we see investment expectations turn sour as a reaction to the declining consumption from Period 4 and the lost export markets. Exports continue to decline and the external balance moves towards deficit (with some offset from the declining imports as a result of lost national income). Together GDP growth falls further and we have a technical recession (two consecutive periods of negative GDP growth).

With unemployment now rising (by implication) the government reacts by increasing government spending and the budget moves into deficit but still within the Maastricht rules. Taxation revenue continues to fall. So the increase in the deficit is partly due to the automatic stabilisers and partly because discretionary fiscal policy is now expanding.

Period 6, exports and investment spending decline further and the government now senses a crisis is on their hands and they accelerate government spending. This starts to reduce the negative GDP growth but pushes the deficit beyond the Maastricht limits of 3 per cent of GDP. Note the rising deficits allows for an improvement in the private domestic balance, although that is also due to the falling investment.

In Period 7, even though exports continue to decline (and the external balance moves into deficit), investors feel more confident given the economy is being supported by growth in the deficit which has arrested the recession. We see a return to positive GDP growth in this period and by implication rising employment, falling unemployment and better times. But the deficit is now well beyond the Maastricht rules and rising even further.

In Period 8, exports decline further but the domestic recovery is well under way supported by the stimulus package and improving investment. We now have an external deficit, rising budget deficit (4.4 per cent of GDP) and rising investment and consumption.

At this point the EMU bosses take over and tell the country that it has to implement an austerity package to get their fiscal parameters back inside the Maastricht rules. So in Period 9, even though investment continues to grow (on past expectations of continued growth in GDP) and the export rout is now stabilised, we see negative GDP growth as government spending is savaged to fit the austerity package agree with the EMU bosses. Net exports moves towards surplus because of the plunge in imports.

Finally, in period 10 the EMU bosses are happy in their warm cosy offices in Brussels or Frankfurt or wherever they have their secure, well-paid jobs because the budget deficit is now back inside the Maastricht rules (2.9 per cent of GDP). Pity about the economy – it is back in a technical recession (a double-dip).

Investment spending has now declined again courtesy of last period’s stimulus withdrawal, consumption is falling, government support of saving is in decline, and we would see employment growth falling and unemployment rising.

The following blogs may be of further interest to you:

• Back to basics – aggregate demand drives output
• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!

Question 5: Premium Question

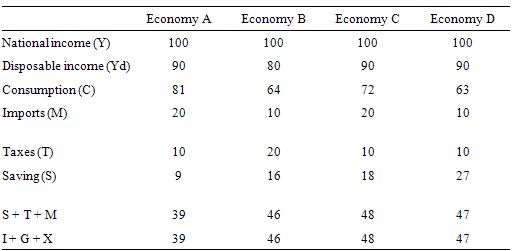
Consider the following table which describes four different economies in terms of the behavioural parameters relating to the leakages to aggregate demand.

Assume that in all four economies, there is idle capacity, the central bank holds all interest rates constant, inflation is constant and there is no changes in international competitiveness.

Which economy would deliver the largest national income bonus for a given discretionary expansion in government spending.

The answer is Economy A.

This question requires you to understand the impact of the different leakages (drains) to aggregate demand that arise from household saving, government taxation and import expenditure.

These leakages combine to determine the spending multiplier.

Students begin to learn about the expenditure multiplier in a very simple model without government or external sector. It sets them up immediately to disregard the crucial relationship between government and non-government sector that really drives the dynamics of the monetary system.

In the text book that Randy Wray and I are currently working on the government/non-government relationship is introduced at the beginning of the learning process to ensure students understand the importance of net positions etc.

So I don’t think it is too hard to explain the expenditure multiplier with government spending, taxes and imports introduced from the start.

The clue is to first of all realise that aggregate demand drives output with generates incomes (via payments to the productive inputs). I won’t go into controversies here about whether the productive inputs are rewarded fairly or whether surplus value is expropriated etc. That is a separate and not unimportant discussion but not germane here to understand the accounting and the dynamics.

Accordingly, what is spent will generate income in that period which is available for use. The uses are further consumption; paying taxes and/or buying imports. We consider imports as a separate category (even though they reflect consumption, investment and government spending decisions) because they constitute spending which does not recycle back into the production process. They are thus considered to be “leakages” from the expenditure system.

So if for every dollar produced and paid out as income, if the economy imports around 20 cents in the dollar, then only 80 cents is available within the system for spending in subsequent periods excluding taxation considerations.

However there are two other “leakages” which arise from domestic sources – saving and taxation. Take taxation first. When income is produced, the households end up with less than they are paid out in gross terms because the government levies a tax. So the income concept available for subsequent spending is called disposable income (Yd).

To keep it simple, imagine a proportional tax of 20 cents in the dollar is levied, so if $100 of income is generated, $20 goes to taxation and Yd is $80 (what is left). So taxation (T) is a “leakage” from the expenditure system in the same way as imports are.

Finally consider saving. Consumers make decisions to spend a proportion of their disposable income. The amount of each dollar they spent at the margin (that is, how much of every extra dollar to they consume) is called the marginal propensity to consume. If that is 0.80 then they spent 80 cents in every dollar of disposable income.

So if total disposable income is $80 (after taxation of 20 cents in the dollar is collected) then consumption (C) will be 0.80 times $80 which is $64 and saving will be the residual – $26. Saving (S) is also a “leakage” from the expenditure system.

It is easy to see that for every $100 produced, the income that is generated and distributed results in $64 in consumption and $36 in leakages which do not cycle back into spending.

For income to remain at $100 in the next period the $36 has to be made up by what economists call “injections” which in these sorts of models comprise the sum of investment (I), government spending (G) and exports (X). The injections are seen as coming from “outside” the output-income generating process (they are called exogenous or autonomous expenditure variables).

Investment is dependent on expectations of future revenue and costs of borrowing. Government spending is clearly a reflection of policy choices available to government. Exports are determined by world incomes and real exchange rates etc.

For GDP to be stable injections have to equal leakages (this can be converted into growth terms to the same effect). The national accounting statements that we have discussed previous such that the government deficit (surplus) equals $-for-$ the non-government surplus (deficit) and those that decompose the non-government sector in the external and private domestic sectors is derived from these relationships.

So imagine there is a certain level of income being produced – its value is immaterial. Imagine that the central bank sees no inflation risk and so interest rates are stable as are exchange rates and domestic wage levels (these simplifications are to to eliminate unnecessary complexity).

The question then is: what would happen if government increased spending by, say, $100? This is the terrain of the multiplier. If aggregate demand increases drive higher output and income increases then the question is by how much?

The spending multiplier is defined as the change in real income that results from a dollar change in exogenous aggregate demand (so one of G, I or X). We could complicate this by having autonomous consumption as well but the principle is not altered.

The spending multiplier is the extra spending that would occur when an autonomous expenditure source changes. So we ask the question: What would be the change in income if I or G or X changed by $1?

To derive the multiplier we need to write out the aggregate demand model and substitute the behavioural parameters into the model.

Aggregate demand (and income)

Y = C + I + G + X – M

Taxes

T = t*Y.

The little t is the marginal tax rate which in this case is the proportional rate. Note here taxes are taken out of total income (Y) which then defines disposable income.

The * sign denotes multiplication. You can do this example in a spreadsheet if you like.

Yd = (1-t)*Y

Consumption and Saving

We define the consumption relationship at the most simple level as a proportional relationship to disposable income (Yd).

C = c*Yd

where little c is the marginal propensity to consume (MPC) or the fraction of every dollar of disposable income consumed.

So using the Yd relationship we can write consumption as:

C = c*(1-t)*Y

Imports

Imports (M) are considered proportional to total income (Y):

M= m*Y

where little m is the marginal propensity to import which is the increase in imports for every real GDP dollar produced.

Multiplier

To derive the multiplier formula we can assemble the aggregate demand relationship with its individual behavioural components as follows:

Y = C + I + G + X – M

Y = c*(1-t)*Y + I + G + X – m*Y

Now, re-arrange the equation to collect the Y terms on the left-hand side:

Y – c*(1-t)*Y + m*Y = I + G + X

You can see the exogenous injections to aggregate demand (those not reliant on national income) are on the right-hand side and all the components of expenditure that rely on national income are collected on the left-hand side.

We simplify this as follows:

Y(1 – c*(1-t)*Y + m) = I + G + X

So the relationship between changes in Y and changes in the exogenous spending components is:

Y = [1/(1 – c*(1-t)*Y + m)]*(I + G + X)

The term in [] brackets on the right-hand side is the multiplier because it shows how much a given change in (I + G + X) multiply to national income Y.

We could write this as:

Y = k*(I + G + X)

where

k = [1/(1 – c*(1-t)*Y + m)]

Or using other symbols:

k = 1/(1 – MPC x (1-t) + MPM)

So the higher is the MPC the lower is the tax rate (t) and the lower is the MPM the higher is the multiplier. That makes sense because taxes and imports drain spending from the income generating system. So as income responds positively to an autonomous injection, the smaller are the drains via taxation and imports and the higher the induced consumption – the higher is the second round spending effect which then continues to generate further income increases.

We can then apply this knowledge to the four economies in the Table. The bottom row of the Table provide the solution to the multiplier for the given parameters.

We interpret the data as follows. If government spending increased by $1, then the total change in national income in Economy A would be $2.56, in Economy B $2.17, in Economy C $2.08, and in Economy D $2.13.

The question obviously requires you to think about the different impacts of varying the drains on aggregate demand. The drains are not all equal.

For example, a given change in the marginal propensity to import has a greater impact than a given change in the marginal propensity to consume as you can see by comparing Economy C to Economy D. This is because imports come out of pre-tax income whereas the consumption decision comes out of disposable income.

A rise in the marginal propensity to consume of 0.1 will more than offset the draining impact of an equal rise in the tax rate because the decline in saving is greater than the rise in taxes.

You can construct all sorts of different scenarios to understand the impacts. To give you an idea of the different compositions of aggregate demand and the different leakages and injections the following Table assumes national income is 100 and then solves the model for each economy given the parameters.

I could clearly make the model more complex but the results would not be very different. Some will suggest the model is overly simplistic because it is a “fixed price” model and assumes supply will just meet any new nominal spending. That is true by construction and is a reasonable description of the state of play at present.

There is no inflation threat at present due to the vast quantities of idle resources that can be brought into production should there be a demand for their services.

Some might argue the external sector is too simplistic and that the terms of trade (real exchange rate) should be included in the export and import relationships. In a complex model that is true but in the context of this model the likely changes would just reinforce the results I derive. There is no loss of insight by holding the terms of trade constant.

Some might argue that the interest rate should be modelled and I reply why? The implicit assumption is that the central bank sets the interest rate and it is currently low in most nations and has been for some years. With no real inflation threat, the short-term rates will remain low for some time yet.

As to long rates (and the rising budget deficit) – show me where the significant rises in budget deficits (for a sovereign nation) are driving up rates. They have actually been falling as a consequence of very strong demand for public debt issues (almost insatiable) by bond markets and the quantitative easing efforts of the large central banks.

For an EMU nation, long-rates are within the control of the ECB as has been demonstrated once it started buying government bonds in the secondary markets. So leaving monetary policy implicit and fixed in this model doesn’t lose any insight or “fix” the results in my favour.

You may wish to read the following blogs for more information:

• Spending multipliers
• Saturday Quiz – October 16, 2010 – answers and discussion

That is enough for today!