Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern…
Saturday Quiz – November 21, 2015 – answers and discussion
Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.
Question 1:
Assume that the current account deficit of a nation is on average over the business cycle equal to 2 per cent of GDP and that the government manages to run a balanced fiscal position when averaged over the same cycle. We can conclude that on average the private domestic sector overall is spending more than it is earning.
The answer is True.
Note that this question doesn’t investigate how the economy might get into this situation. But whatever behavioural forces were at play, the sectoral balances all have to sum to zero. Once you understand that, then deduction leads to the correct answer.
To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X – M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).
From the uses perspective, national income (GDP) can be used for:
GDP = C + S + T
which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.
Equating these two perspectives we get:
C + S + T = GDP = C + I + G + (X – M)
So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.
(I – S) + (G – T) + (X – M) = 0
That is the three balances have to sum to zero. The sectoral balances derived are:
- The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
- The Fiscal Deficit (G – T) – negative if in surplus, positive if in deficit.
- The Current Account balance (X – M) – positive if in surplus, negative if in deficit.
These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.
A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).
This is also a basic rule derived from the national accounts and has to apply at all times.
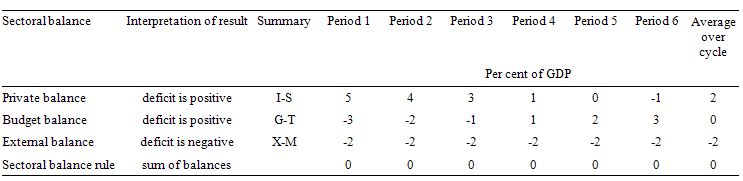
To help us answer the specific question posed, the following Table shows a stylised business cycle with some simplifications. The economy is running a surplus in the first three periods (but declining) and then increasing deficits. Over the entire cycle the balanced fiscal rule would be achieved as the fiscal balances average to zero. So the deficits are covered by fully offsetting surpluses over the cycle.
The simplification is the constant external deficit (that is, no cyclical sensitivity) of 2 per cent of GDP over the entire cycle. You can then see what the private domestic balance is doing clearly. When the fiscal balance is in surplus, the private balance is in deficit. The larger the fiscal surplus the larger the private deficit for a given external deficit.
As the fiscal position moves into deficit, the private domestic balance approaches balance and then finally in Period 6, the fiscal deficit is large enough (3 per cent of GDP) to offset the demand-draining external deficit (2 per cent of GDP) and so the private domestic sector can save overall. The fiscal deficits are underpinning spending and allowing income growth to be sufficient to generate savings greater than investment in the private domestic sector.
On average over the cycle, under these conditions (balanced public fiscal position) the private domestic deficit exactly equals the external deficit. As a result over the course of the business cycle, the private domestic sector is spending more than it is earning. This could be via increasing indebtedness or running down previous savings or asset accumulation.
The following blogs may be of further interest to you:
- Barnaby, better to walk before we run
- Stock-flow consistent macro models
- Norway and sectoral balances
- The OECD is at it again!
Question 2:
Trade unions that manage to push aggregate wages growth ahead of the inflation rate will ensure that workers gain a greater share of national income.
The answer is False.
Workers may enjoy a rising wage share as real wages rise but not necessarily.
The wage share in nominal GDP is expressed as the total wage bill as a percentage of nominal GDP. Economists differentiate between nominal GDP ($GDP), which is total output produced at market prices and real GDP (GDP), which is the actual physical equivalent of the nominal GDP. We will come back to that distinction soon.
To compute the wage share we need to consider total labour costs in production and the flow of production ($GDP) each period.
Employment (L) is a stock and is measured in persons (averaged over some period like a month or a quarter or a year.
The wage bill is a flow and is the product of total employment (L) and the average wage (w) prevailing at any point in time. Stocks (L) become flows if it is multiplied by a flow variable (W). So the wage bill is the total labour costs in production per period.
So the wage bill = W.L
The wage share is just the total labour costs expressed as a proportion of $GDP – (W.L)/$GDP in nominal terms, usually expressed as a percentage. We can actually break this down further.
Labour productivity (LP) is the units of real GDP per person employed per period. Using the symbols already defined this can be written as:
LP = GDP/L
so it tells us what real output (GDP) each labour unit that is added to production produces on average.
We can also define another term that is regularly used in the media – the real wage – which is the purchasing power equivalent on the nominal wage that workers get paid each period. To compute the real wage we need to consider two variables: (a) the nominal wage (W) and the aggregate price level (P).
We might consider the aggregate price level to be measured by the consumer price index (CPI) although there are huge debates about that. But in a sense, this macroeconomic price level doesn’t exist but represents some abstract measure of the general movement in all prices in the economy.
Macroeconomics is hard to learn because it involves these abstract variables that are never observed – like the price level, like “the interest rate” etc. They are just stylisations of the general tendency of all the different prices and interest rates.
Now the nominal wage (W) – that is paid by employers to workers is determined in the labour market – by the contract of employment between the worker and the employer. The price level (P) is determined in the goods market – by the interaction of total supply of output and aggregate demand for that output although there are complex models of firm price setting that use cost-plus mark-up formulas with demand just determining volume sold. We shouldn’t get into those debates here.
The inflation rate is just the continuous growth in the price level (P). A once-off adjustment in the price level is not considered by economists to constitute inflation.
So the real wage (w) tells us what volume of real goods and services the nominal wage (W) will be able to command and is obviously influenced by the level of W and the price level. For a given W, the lower is P the greater the purchasing power of the nominal wage and so the higher is the real wage (w).
We write the real wage (w) as W/P. So if W = 10 and P = 1, then the real wage (w) = 10 meaning that the current wage will buy 10 units of real output. If P rose to 2 then w = 5, meaning the real wage was now cut by one-half.
So the proposition in the question – that nominal wages grow faster than inflation – tells us that the real wage is rising.
Nominal GDP ($GDP) can be written as P.GDP, where the P values the real physical output.
Now if you put of these concepts together you get an interesting framework. To help you follow the logic here are the terms developed and be careful not to confuse $GDP (nominal) with GDP (real):
- Wage share = (W.L)/$GDP
- Nominal GDP: $GDP = P.GDP
- Labour productivity: LP = GDP/L
- Real wage: w = W/P
By substituting the expression for Nominal GDP into the wage share measure we get:
Wage share = (W.L)/P.GDP
In this area of economics, we often look for alternative way to write this expression – it maintains the equivalence (that is, obeys all the rules of algebra) but presents the expression (in this case the wage share) in a different “view”.
So we can write as an equivalent:
Wage share – (W/P).(L/GDP)
Now if you note that (L/GDP) is the inverse (reciprocal) of the labour productivity term (GDP/L). We can use another rule of algebra (reversing the invert and multiply rule) to rewrite this expression again in a more interpretable fashion.
So an equivalent but more convenient measure of the wage share is:
Wage share = (W/P)/(GDP/L) – that is, the real wage (W/P) divided by labour productivity (GDP/L).
I won’t show this but I could also express this in growth terms such that if the growth in the real wage equals labour productivity growth the wage share is constant. The algebra is simple but we have done enough of that already.
That journey might have seemed difficult to non-economists (or those not well-versed in algebra) but it produces a very easy to understand formula for the wage share.
Two other points to note. The wage share is also equivalent to the real unit labour cost (RULC) measures that Treasuries and central banks use to describe trends in costs within the economy. Please read my blog – Saturday Quiz – May 15, 2010 – answers and discussion – for more discussion on this point.
Now it becomes obvious that if the nominal wage (W) grows faster than the price level (P) then the real wage is growing. But that doesn’t automatically lead to a growing wage share. So the blanket proposition stated in the question is false.
If the real wage is growing at the same rate as labour productivity, then both terms in the wage share ratio are equal and so the wage share is constant.
If the real wage is growing but labour productivity is growing faster, then the wage share will fall.
Only if the real wage is growing faster than labour productivity , will the wage share rise.
Question 3:
If labour productivity is growing at 2 per cent per annum and the labour force is growing at 1.5 per cent per annum and the average working week is constant in hours, then real GDP growth must be greater than 3.5 per cent per annum or unemployment will rise.
The answer is False.
The facts are:
- Labour productivity growth (that is, growth in real output per person employed) growing at 2 per cent per annum. So as this grows less employment in required per unit of output.
- The labour force is growing by 1.5 per cent per annum. Growth in the labour force adds to the employment that has to be generated for unemployment to stay constant (or fall).
- The average working week is constant in hours. So firms are not making hours adjustments up or down with their existing workforce. Hours adjustments alter the relationship between real GDP growth and persons employed.
Real GDP growth doesn’t relate to the labour market in any direct way. The late Arthur Okun is famous (among other things) for estimating the relationship that links the percentage deviation in real GDP growth from potential to the percentage change in the unemployment rate – the so-called Okun’s Law.
The algebra underlying this law can be manipulated to estimate the evolution of the unemployment rate based on real output forecasts.
From Okun, we can relate the major output and labour force aggregates to form expectations about changes in the aggregate unemployment rate based on output growth rates. A series of accounting identities underpins Okun’s Law and helps us, in part, to understand why unemployment rates have risen.
Take the following output accounting statement:
(1) Y = LP*(1-UR)LH
where Y is real GDP, LP is labour productivity in persons (that is, real output per unit of labour), H is the average number of hours worked per period, UR is the aggregate unemployment rate, and L is the labour force. So (1-UR) is the employment rate, by definition.
Equation (1) just tells us the obvious – that total output produced in a period is equal to total labour input [(1-UR)LH] times the amount of output each unit of labour input produces (LP).
Using some simple calculus you can convert Equation (1) into an approximate dynamic equation expressing percentage growth rates, which in turn, provides a simple benchmark to estimate, for given labour force and labour productivity growth rates, the increase in output required to achieve a desired unemployment rate.
Accordingly, with small letters indicating percentage growth rates and assuming that the average number of hours worked per period is more or less constant, we get:
(2) y = lp + (1 – ur) + lf
Re-arranging Equation (2) to express it in a way that allows us to achieve our aim (re-arranging just means taking and adding things to both sides of the equation):
(3) ur = 1 + lp + lf – y
Equation (3) provides the approximate rule of thumb – if the unemployment rate is to remain constant, the rate of real output growth must equal the rate of growth in the labour force plus the growth rate in labour productivity.
It is an approximate relationship because cyclical movements in labour productivity (changes in hoarding) and the labour force participation rates can modify the relationships in the short-run. But it provides reasonable estimates of what happens when real output changes.
The sum of labour force and productivity growth rates is referred to as the required real GDP growth rate – required to keep the unemployment rate constant.
Remember that labour productivity growth (real GDP per person employed) reduces the need for labour for a given real GDP growth rate while labour force growth adds workers that have to be accommodated for by the real GDP growth (for a given productivity growth rate).
So in the example, the required real GDP growth rate is 3.5 per cent per annum.
The question therefore posed that if the real GDP growth equal to 3.5 per cent per annum or less would the unemployment rate rise.
All we can say from the information presented is that the unemployment rate would be constant if the real GDP growth rate was 3.5 per cent.
The unemployment rate will rise if real GDP growth is less than 3.5 per cent (given the facts) because real output growth would not be strong enough to absorb the new entrants into the labour market and offset the employment losses arising from labour productivity growth.
Similarly, the unemployment rate would fall if real GDP growth is more than 3.5 per cent for the opposite reasons.
But this tells us nothing about what is happening with unemployment. Unemployment would still be rising if employment growth was exactly equal to labour force growth even though the unemployment rate would be constant.
The following blog may be of further interest to you:
I don’t follow the explanation for the answer given to Q3.
If GDP growth rate is 3.5% then I see that given the assumptions the unemployment rate will remain constant and the actual number of unemployed will increase (unless the unemployment rate is 0%). To keep the number of unemployed constant you would need GDP rate somewhere above 3.5%. It is certain that (with your assumptions) that any rate of GDP growth 3.5% or less will lead to increased unemployment, while some (but not all) rates above 3.5% will lead to unemployment falling.
So the statement “the real GDP growth must be greater than 3.5 per cent per annum or unemployment will rise” is true. The fact that “some rates greater than 3.5 per cent will lead to rising unemployment” does not falsify it.
Hi Bill,
Not a question on the test, but is relevant to the identity expressions in Q1.
I would really like to know what you make of the 3-part “Fiscal fallacies and sectoral balances” posts made by Geoff Tily in his blog?
The latest is here…
http://touchstoneblog.org.uk/2015/11/fiscal-fallacies-and-sectoral-balances-response-to-the-critics/
NB: Geoff is currently the TUC’s Senior Economist, and was formerly a macroeconomic adviser to HM Treasury.
The reason I ask is that Geoff’s work has been cited by Ann Pettifor as evidence supporting her view that “The concept of sectoral balances belongs to the sphere of accounting, not economics”.
https://twitter.com/annpettifor/status/659724668513972224
Hi
Stephen Ferguson: “I would really like to know what you make of the 3-part “Fiscal fallacies and sectoral balances” posts made by Geoff Tily in his blog?”.
I very much second that request. If I recall correctly, others have stated that the sectoral balances framework has often proven a useful starting point in explaining to their families + friends about the logic of MMT and about the folly of arguments for austerity. If one of Jeremy Corbyn’s advisors (Anne Pettifor) is needlessly preventing the left from utilising such a persuasive argument, this is very troubling.
Stephen Ferguson, A.J. Miles,
While waiting for Bill to reply, I was reading Geoff Tily’s series of blog posts just now. I honestly believe he conjures up a spat where none exists.
His main point is that by themselves sectoral balances do not tell us about the interactions between sectors and therefore we should avoid extracting too many conclusions out of them. Indeed, this is true for all accounting identities.
He also points out that gross flows are more important (again, they usually are) than the balances themselves, as (let’s say) a rise in government spending (G) can in itself regenerate higher tax revenues (T) and leave the public sector balance unchanged while still stimulating the economy. The example he gives is the opposite: Osborne may cut G but this can express itself as a reduction in T rather than the other balances moving. But then the economy would slow. He underscores Keynes’ point was never about balances (“deficit spending”) but rather fiscal multipliers.
Again, this is creating controversy where none should exist. I don’t believe Bill (or Hyman Minsky for that matter) ever said sectoral balances explain causal phenomenons of any kind (neither do current account relationships between countries for that matter, but that’s another story). Rather, they uncover logical fallacies when they are violated.
So Osborne CLAIMS he can at the same time cut G and reduce the government budget balance to zero. If he is right, other balances (current account, businesses, households) must by definition change. So either:
a) Current account deficit will fall.
b) Business balance surplus will narrow.
c) Household budget deficit will widen.
d) A combination of the three above.
e) Osborne will fail to reduce the government budget deficit. That is, GDP growth will tank.
Again, we don’t know which will happen. If somebody using sectoral balance analysis claims he/she does he/she is bullshitting. Bur what cannot happen is a cut in any gross flow with no change.
Excuse my confusion; I am only beginning to study MMT. Question 1 leaves me with this head scratcher: I seem to have learned that surpluses must be offset by deficits among the sectors. So if the external sector is in deficit, and the government sector is balanced (showing neither a surplus nor a deficit), then would not the private sector have to show a surplus? Where have I got things wrong?
Lector, I believe it’s the use of the “external sector is in deficit” phrase that confuses you. In this case, Bill uses the phrase to mean the domestic economy is in deficit with the rest of the world (current account balance is negative). That is, the rest of the world has a surplus, it is accumulating financial assets in the domestic economy.
If the public sector doesn’t provide those assets in form of government bonds (or central bank reserves, if spending is not sterilized via bond sales), then they must be getting them on a net basis from the private sector. That is, the private sector must be in deficit.
Mnementh,
Thank you for your reply.
I still have difficulties. The first question of the Saturday quiz above refers to a three sector model. However, you seem to add a fourth sector: “the rest of the world.”
A total beginner concerning MMT, at the moment, I am reading Wray’s excellent “Modern Money Theory,” where he stresses on page 14 of the 2015 edition
“the important accounting principle that if we sum the deficits run by one or more sectors, this must equal the surpluses run by the other sector(s).”
This is what lingered in my mind when I posted my above admission of being confused.
Mnementh,
Apologies: you are not introducing a new sector, unlike I had presumed in my last comment. Your explanation is convincing.
Thanks for help.