Saturday Quiz – July 12, 2014 – answers and discussion

July 13, 2014
bill
Saturday quiz
0 Comments

Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

Over a given business cycle (peak to peak), if a nation’s external sector is on average balanced and the government gap between its tax revenue and spending is, on average, equal to 1 per cent of GDP, then the private domestic sector’s spending-income balance will on average be in:

(a) Deficit of 1 per cent of GDP

(b) Surplus of 1 per cent of GDP

The answer is Deficit of 1 per cent of GDP.

This is a question about sectoral balances. Skip the derivation if you are familiar with the framework.

First, you need to understand the basic relationship between the sectoral flows and the balances that are derived from them. The flows are derived from the National Accounting relationship between aggregate spending and income. So:

(1) Y = C + I + G + (X – M)

where Y is GDP (income), C is consumption spending, I is investment spending, G is government spending, X is exports and M is imports (so X – M = net exports).

Another perspective on the national income accounting is to note that households can use total income (Y) for the following uses:

(2) Y = C + S + T

where S is total saving and T is total taxation (the other variables are as previously defined).

You than then bring the two perspectives together (because they are both just “views” of Y) to write:

(3) C + S + T = Y = C + I + G + (X – M)

You can then drop the C (common on both sides) and you get:

(4) S + T = I + G + (X – M)

Then you can convert this into the familiar sectoral balances accounting relations which allow us to understand the influence of fiscal policy over private sector indebtedness.

So we can re-arrange Equation (4) to get the accounting identity for the three sectoral balances – private domestic, government fiscal balance and external:

(S – I) = (G – T) + (X – M)

The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.

Another way of saying this is that total private savings (S) is equal to private investment (I) plus the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.

All these relationships (equations) hold as a matter of accounting and not matters of opinion.

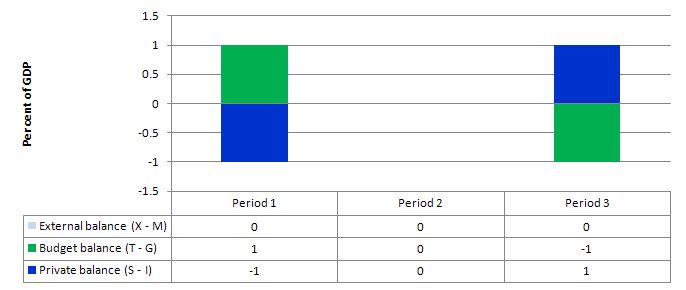
Consider the following graph which shows three situations where the external sector is in balance.

Period 1, is the case in point with the fiscal balance in surplus (T – G = 1) and the private balance is in deficit (S – I = -1). With the external balance equal to 0, the general rule that the government surplus (deficit) equals the non-government deficit (surplus) applies to the government and the private domestic sector. In other words, the private domestic sector must be spending ore than it is earning (a deficit).

In Period 3, the fiscal balance is in deficit (T – G = -1) and this provides some demand stimulus in the absence of any impact from the external sector, which allows the private domestic sector to save (S – I = 1).

Period 2, the fiscal balance is in balance (T – G = 0) and so the private domestic sector must also be in balance (spending equals its earning).

The movements in income associated with the spending and revenue patterns will ensure these balances arise. The problem is that if the private domestic sector desires to save overall then this outcome will be unstable and would lead to changes in the other balances as national income changed in response to the decline in private spending.

So under the conditions specified in the question, the private domestic sector cannot save. The government would be undermining any desire to save by not providing the fiscal stimulus necessary to increase national output and income so that private households/firms could save.

You may wish to read the following blogs for more information:

Question 2:

Considering only the initial impact on national income (ignoring multiplier effects), fiscal austerity will have a greater negative effect on real GDP if it manifests as a spending cut of $x than if the government chose to raise a value added tax to generate $x revenue at the current level of national income.

The answer is True.

The question is only seeking an understanding of the initial drain on the spending stream rather than the fully exhausted multiplied contraction of national income that will result. It is clear that the tax increase increase will have two effects: (a) some initial demand drain; and (b) it reduces the value of the multiplier, other things equal.

We are only interested in the first effect rather than the total effect. But I will give you some insight also into what the two components of the tax result might imply overall when compared to the impact on demand motivated by an decrease in government spending.

To give you a concrete example which will consolidate the understanding of what happens, imagine that the marginal propensity to consume out of disposable income is 0.8 and there is only one tax rate set at 0.20. So for every extra dollar that the economy produces the government taxes 20 cents leaving 80 cents in disposable income. In turn, households then consume 0.8 of this 80 cents which means an injection of 64 cents goes into aggregate demand which them multiplies as the initial spending creates income which, in turn, generates more spending and so on.

Government spending cut

A cut in government spending (say of $1000) is what we call an exogenous withdrawal from the aggregate spending stream and this directly reduces aggregate demand by that amount. So it might be the cancellation of a long-standing order for $1000 worth of gadget X. The firm that produces gadget X thus reduces production of the good or service by the fall in orders ($1000) (if they deem the drop in sales to be permanent) and as a result incomes of the productive factors working for and/or used by the firm fall by $1000. So the initial fall in aggregate demand is $1000.

This initial fall in national output and income would then induce a further fall in consumption by 64 cents in the dollar so in Period 2, aggregate demand would decline by $640. Output and income fall further by the same amount to meet this drop in spending. In Period 3, aggregate demand falls by 0.8 x 0.8 x $640 and so on. The induced spending decrease gets smaller and smaller because some of each round of income drop is taxed away, some goes to a decline in imports and some manifests as a decline in saving.

Tax-increase induced contraction

The contraction coming from a tax-cut does not directly impact on the spending stream in the same way as the cut in government spending.

First, imagine the government worked out a tax rise cut that would reduce its initial fiscal deficit by the same amount as would have been the case if it had cut government spending (so in our example, $1000).

In other words, disposable income at each level of GDP falls initially by $1000. What happens next?

Some of the decline in disposable income manifests as lost saving (20 cents in each dollar that disposable income falls in the example being used). So the lost consumption is equal to the marginal propensity to consume out of disposable income times the drop in disposable income (which if the MPC is less than 1 will be lower than the $1000).

In this case the reduction in aggregate demand is $800 rather than $1000 in the case of the cut in government spending.

What happens next depends on the parameters of the macroeconomic system. The multiplied fall in national income may be higher or lower depending on these parameters. But it will never be the case that an initial fiscal equivalent tax rise will be more damaging to national income than a cut in government spending.

Note in answering this question I am disregarding all the nonsensical notions of Ricardian equivalence that abound among the mainstream economists. I am also ignoring the empirically-questionable mainstream claims that tax increases erode work incentives which force workers to supply less labour. In this case, I avoid those issues by imposing a value-added tax increase.

You may wish to read the following blogs for more information:

Spending multipliers

Question 3:

During a recession, if the government uses expansionary fiscal policy to restore trend real GDP growth it will restore full employment.

The answer is False.

To see why, we might usefully construct a scenario that will explicate the options available to a government:

Trend real GDP growth rate is 3 per cent annum.
Labour productivity growth (that is, growth in real output per person employed) is growing at 2 per cent per annum. So as this grows less employment in required per unit of output.
The labour force is growing by 1.5 per cent per annum. Growth in the labour force adds to the employment that has to be generated for unemployment to stay constant (or fall).
The average working week is constant in hours. So firms are not making hours adjustments up or down with their existing workforce. Hours adjustments alter the relationship between real GDP growth and persons employed.

We can use this scenario to explore the different outcomes.

The trend rate of real GDP growth doesn’t relate to the labour market in any direct way. The late Arthur Okun is famous (among other things) for estimating the relationship that links the percentage deviation in real GDP growth from potential to the percentage change in the unemployment rate – the so-called Okun’s Law.

The algebra underlying this law can be manipulated to estimate the evolution of the unemployment rate based on real output forecasts.

From Okun, we can relate the major output and labour force aggregates to form expectations about changes in the aggregate unemployment rate based on output growth rates. A series of accounting identities underpins Okun’s Law and helps us, in part, to understand why unemployment rates have risen.

Take the following output accounting statement:

(1) Y = LP*(1-UR)LH

where Y is real GDP, LP is labour productivity in persons (that is, real output per unit of labour), H is the average number of hours worked per period, UR is the aggregate unemployment rate, and L is the labour force. So (1-UR) is the employment rate, by definition.

Equation (1) just tells us the obvious – that total output produced in a period is equal to total labour input [(1-UR)LH] times the amount of output each unit of labour input produces (LP).

Using some simple calculus you can convert Equation (1) into an approximate dynamic equation expressing percentage growth rates, which in turn, provides a simple benchmark to estimate, for given labour force and labour productivity growth rates, the increase in output required to achieve a desired unemployment rate.

Accordingly, with small letters indicating percentage growth rates and assuming that the average number of hours worked per period is more or less constant, we get:

(2) y = lp + (1 – ur) + lf

Re-arranging Equation (2) to express it in a way that allows us to achieve our aim (re-arranging just means taking and adding things to both sides of the equation):

(3) ur = 1 + lp + lf – y

Equation (3) provides the approximate rule of thumb – if the unemployment rate is to remain constant, the rate of real output growth must equal the rate of growth in the labour force plus the growth rate in labour productivity.

It is an approximate relationship because cyclical movements in labour productivity (changes in hoarding) and the labour force participation rates can modify the relationships in the short-run. But it provides reasonable estimates of what happens when real output changes.

The sum of labour force and productivity growth rates is referred to as the required real GDP growth rate – required to keep the unemployment rate constant.

Remember that labour productivity growth (real GDP per person employed) reduces the need for labour for a given real GDP growth rate while labour force growth adds workers that have to be accommodated for by the real GDP growth (for a given productivity growth rate).

So in the example, the required real GDP growth rate is 3.5 per cent per annum and if policy only aspires to keep real GDP growth at its trend growth rate of 3 per cent annum, then the output gap that emerges is 0.5 per cent per annum.

The unemployment rate will rise by this much (give or take) and reflects the fact that real output growth is not strong enough to both absorb the new entrants into the labour market and offset the employment losses arising from labour productivity growth.

So the appropriate fiscal strategy does not relate to “trend output” but to the required real GDP growth rate given labour force and productivity growth. The two growth rates might be consistent but then they need not be. That lack of concordance makes the proposition false.

The following blog may be of further interest to you: