I am still catching up after being away in the UK last week. I will…
The ARRA created 1.503 million jobs
Econometricians seek to use sample data (that is, data drawn from some population) to derive (estimate) unknown parameters that define a relationship between two or more variables. So we might say that consumption (C) depends on income (Y) subject to some constant amount of consumption (a). We initially do not know what the dependency between C and Y is except we hypothesise it is positive and logically lies between 0 and 1 over a long period. We might write this as C = a + bY. The parameter b tells us how much consumption rises when income rises by say a dollar. If b = 0.8, then for every extra dollar received a consumer will spend 80 cents of it. Economists refer to this parameter as the marginal propensity to consume. The econometrician is then hired to estimate the value of the parameters a and b that the economist has theorised about (the two roles are usually embedded in the same person!). So the econometrician seeks to obtain what are called point estimates of the “unknown” parameters (a, b). Given statistical techniques are used, sampling variation is taken into account by the standard error of the point estimate and it is the measure of the precision of the point estimate. A small standard error relative to the estimated parameter value indicates higher precision. The standard errors are used in two ways. First, statisticians have formulated “tests of significance” with appropriate summary test statistics which measure (broadly) when we might consider the estimated parameters (or coefficients) to be the value gained as against zero. We say a coefficient is statistically significant if the “test statistic” passes some criteria. If an estimate is found to be not statistically significant then we conclude the value is zero (no relationship) despite the value obtained in the regression. Second, the standard errors form the basis of confidence intervals – that is, how strongly we feel about the point estimates. A narrow confidence interval is better than a wider interval. We derive interval estimates which are a range of values that we feel will contain the “true” parameter based on an arbitrary, pre-assigned probability. Note the term – pre-assigned probability. I will come back to it. There are many methods of estimating the unknown parameters (these methods are called estimators) and each has different properties, relevance to different situations, data types etc. Irrespective of the estimator used, the estimates derived of the unknown parameters will vary from sample to sample. To help us provide some level of confidence in the results gained we construct these interval estimates. The wider the interval the more confident we become that the true parameter value (the one that exists in the population irrespective of the sample taken) lies within the interval. I won’t go into how the confidence intervals are derived but the width of the interval is proportional to the standard error of the estimate – so a larger standard error the wider is the interval. The larger the standard error the less sure we are about the true value of the unknown parameter. This is why we call the standard error a measure of the precision of the estimate – how closely it measures the true population value. To be specific, lets say that we want to be 95 per cent sure that the interval we derive around the point estimate contains the true value (which is tantamount to saying we are interested in knowing just how close the estimate is to the true population value). We use a confidence interval to make that assessment. The confidence interval is constructed after selecting a pre-assigned probability (like 95 per cent or 99 per cent). The interval is demarcated by the upper and lower confidence limits which allow us to compute the range of the interval. We define this interval for a particular level of significance – so for a 95 per cent probability range we adopt a 0.05 level of significance. The lower the level of significance the higher the probability that the estimate will lie within the interval but also the interval becomes narrower. In the trade we say that if the level of significance is 0.05 (or 5 per cent), the probability that the interval so derived contains the true value of the parameter is 95 per cent. That is, in repeated sampling 95 out of 100 intervals constructed will contain the true value. We thus seek to formulate statements expressing our level of confidence. We usually pick some pre-assigned significance value to calculate our interval. But what should that level of significance be? The outcome of our testing (whether an estimated coefficient is of use or not) depends in part on this choice. Here statistical literature gets complicated and talks about Type I (probability of rejecting a true hypothesis) and Type II (probability of accepting a false hypothesis) errors. The choice of the significance is dealt with in depth in the literature on statistical decision making. If we want to reduce a Type I error we increase the chance of committing a Type II error (and vice versa). If we make it easier to avoid a Type I error (by widening the confidence interval) we run the danger of falling into a Type II error (like, the US fiscal initiative – ARRA didn’t create any net jobs). How do we deal with this trade-off? What are the relative costs of committing each type of error? We usually don’t know these relative costs so conventions are used. Econometricians typically use 1 or 5 per cent levels of significance which reduce the confidence interval and the chance of making a Type II error. The bias is typically to make sure we minimise the chance of a Type I error (see here). In my experience, 5 per cent is the norm for my profession. A level of significance of 10 per cent is considered too large because it creates too wide an interval and exposes one to Type II errors too easily. We tell our econometric students to use 5. This has precedence in the early literature – here is an interesting and readable article – Stigler S (2008) “Fisher and the 5% level”. Chance, 21 (4):12. The other point to note is that a researcher usually decides on a level of significance and uses it throughout their career. One gets suspicious when you see a particular individual swapping levels in different papers. If we go back to the hypothesis testing angle – the higher the level of significance the easier it is to accept the null hypothesis that the point estimate is what it is. So if you are really bent on “proving” something then the higher the significance level the more likely you will find the coefficient estimates “statistically significant”. That is why professionals like me get suspicious when you see someone use the 10 per cent level – which is not the industry norm. The first question I ask then is why are they using that level of significance? Often I suspect their motives (especially when in previous papers the same authors use lower levels (typically 5 per cent). While this might have all seemed somewhat opaque I had a purpose. If you were assessing whether a major government fiscal response had been beneficial in terms of providing a net employment boost at a time of crisis you would want to be reasonably confident that you were providing good advice to the government. This is especially the case when the policy space is so contested in political and/or ideological terms. What would you expect to happen in the current climate if you “found” that the major stimulus actually destroyed jobs overall? This sort of conclusion would fuel the conservative fiscal antagonists and probably lead to more politicians calling for austerity (fiscal cutbacks). What happens if you had made a Type II error – you had accepted a false hypothesis – which in this instance could be interpreted as the stimulus was damaging to private employment? I would think that given the gravity of this sort of study, you would want to be very certain that your results were robust. At the very least a 5 per cent level of significance (the norm) would be chosen. Going to a 10 per cent level would be a very odd decision indeed. Which brings me to the recent paper by US academic economists Timothy Conley and Bill Dupor entitled – The American Recovery and Reinvestment Act: Public Sector Jobs Saved, Private Sector Jobs Forestalled – which Greg Mankiw is promoting on his blog without the slightest comment or promotion of rival papers. Mankiw’s motives are clear. If he was to be balanced in disseminating information that provided a debate he would reference other work which has found the opposite results. Conley and Dupor seek to “estimate how many jobs were created/saved” by the spending component of the The American Recovery and Reinvestment Act (ARRA). So they ignore the tax cut component. They rather starkly conclude:
Our benchmark results suggest that the ARRA created/saved approximately 450 thousand state and local government jobs and destroyed/forestalled roughly one million private sector jobs. State and local government jobs were saved because ARRA funds were largely used to oset state revenue shortfalls and Medicaid increases rather than boost private sector employment. The majority of destroyed/forestalled jobs were in growth industries including health, education, professional and business services. This suggests the possibility that, in absence of the ARRA, many government workers (on average relatively well-educated) would have found private-sector employment had their jobs not been saved.So a net loss of 650 thousand jobs. If that was true then we should be very concerned about the capacity of the US government to implement a well-designed fiscal stimulus package. In the light of the above discussion lets consider their results. I could go on about their econometric techniques which are dubious to say the least but I think I would leave the bulk of my readership behind. So for the purposes of discussion lets assume that there are no issues with the way they derived their estimates. Their principle claim is that the ARRA spending was prone to fungability – which as Wikipedia notes “is the property of a good or a commodity whose individual units are capable of mutual substitution”. I will come back to that. The authors say that:
A large fraction of the Federal ARRA dollars was channeled through and controlled by state and local governments … [which] … creates an environment where Federal dollars might be used to replace state and local spending … Upon acquisition of ARRA funds for a specific purpose, a state or local government could cut its own expenditure on that purpose. As a result, these governments could treat the ARRA dollars as general revenue, i.e. the dollars were eectively fungible.That is their main hypothesis. The sub-national levels of government in the US spent the ARRA money “for the same purpose it would have spent its just lost tax dollar. Under this scenario, the relevant treatment is ARRA funding net of state budget shortfalls”. They use this assertion to structure their modelling experiment – which is beyond the discussion of this blog. They claim they test this “restriction” (see Table 5) but provide no information about the significance of that test. At what level do they accept that restriction? It is always poor practice to hide your test diagnostics (significance, degress of freedom etc). But as I said I will leave those quibbles out of this discussion. The following Table is take from Table 4 of the Conley and Dupor paper and shows their main results upon which they draw their principal conclusions.
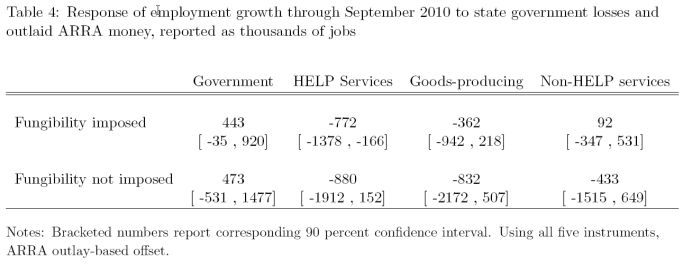If we play by their rules and construct the 90 per cent confidence interval using the bracketed numbers they provide we would come up with this sort of Table. There are several statements we can make about the results.
First, we can be as equally confident that the ARRA produced 1.503 millions jobs overall (which would include nearly a million government jobs) as we would be that it destroyed 2.7 million jobs. That is a very wide confidence interval – and useless for any definitive policy purposes.
Second, anywhere in between -2.7 million and +1.5 million jobs carries equal certainty (at the 10 per cent level). So we could be 90 per cent sure that the ARRA created or destroyed no net jobs just as it created 1.5 million.
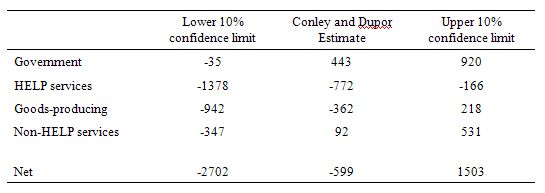What this means is that if we were to conjecture that the ARRA created 1.503 million jobs net then Conley and Dupor’s results would support that conjecture. We would not be able to reject it.
We would also not be able to reject the hypothesis that ARRA created no net jobs. And so on.
The other point is that they depart from the convention and use 10 per cent significance levels for their analysis. Why do they do that? Perhaps to lay claim to more than their results can provide at the conventional level (which is a much more robust test on a model)? Further, why in earlier papers (not about ARRA) do the authors use conventional significance levels?
The later results that the authors present (Tables 7 and 9) do not alter these conclusions.
Further, if you then examine their elasticity results (Table 5) which they say is a “second way to report the jobs effect” you will find that most of their estimates are not statistically significant by conventional standards. That means the estimated coefficients are not different to zero – meaning no statistical effect is found.
The point is that the authors are not entitled to make the conclusions they provide based on the results presented in this paper.
The most extraordinary statement the authors make is that “(i)n the absence of the ARRA, many government employees would have found jobs in the private sector.” So here is a prior question: Why were the private employers laying off workers and creating “vacancies” that could have been filled by the workers who lost their jobs in the public sector?
Conley and Dupor might say because the states were cutting back road construction spending and the like. But then the argument becomes circular.
Why did the states lose revenue in the first place that was “replaced” by ARRA funding which enabled them to maintain public employment levels but cut back private contracts?
The story seems to be something like this. The states lose revenue and cut back public employment and presumably programs. The private sector is hurt and lays of workers. ARRA comes along and provides the top up to the states lost revenue and they use this to substitute for spending they would have already made which allows them to maintain public employment but somehow the private sector still loses its contracts. Why?
What were the public employees doing who presumably serviced these contracts once the states had reduced their contractual exposure?
And – to complete the circle – why did the states lose revenue in the first place
The plausible story which Conley and Dupor avoid is that aggregate demand collapsed in the wake of the financial meltdown. This caused state revenue to collapse and the state to cut back on spending. The federal government refused to provide enough stimulus to match that collapse (by way of a per capita state by state injection) and replace the initial collapse in private spending.
As a consequence, the economy goes into recession and national unemployment rises. The ARRA injection helped put a floor in that collapse in demand but was insufficient to stop the significant decline in economic activity.
The other interesting implication of their paper which they do not comment on is that government spending creates millions of jobs. If their assertions are true, then the only reason the ARRA was ineffective is because the state/local governments substituted the spending. That would be a problem of program design and the rules that accompanied the state-level grants. So it is not a criticism of fiscal policy per se but just the way it was implemented.
I am not saying I agree with that proposition but I was critical of the composition of spending that the US government provided. It was too focused on the top-end-of-town and not employment-centred.
The final point I would make relates to the reason why we study macroeconomics in the first place. Micro-based studies fall prey to fallacy of composition. Please read my blog – Fiscal austerity – the newest fallacy of composition – for more discussion on this point.
Conley and Dupor’s paper is incapable of examining national impacts because it excludes the possibility that stimulus in one state may stimulate activity in another state. Those of us who estimate regional data know full well the problem of so called spatial spillover effects present to researchers trying to isolate regionally-specific and national impacts of policy changes.
So to really understand the overall employment impact of ARRA you have to be able to estimate the state-level effects plus the spatial spillovers.
Conley and Dupor only fleetingly acknowledge this limitation of their work (in their conclusion as a passing comment). They say by way of future research:
The most promising avenue in this regard is to allow for cross-state positive spillovers. This might result in estimates of a large positive jobs effect. Suppose, for example, that Georgia received relatively more ARRA aid, which in turn stimulated that state’s economy. If, as a result, Georgia residents’ vacation spending in Florida increased, then the increased vacationing might generate jobs in Florida. Our methodology cannot pick up this effect. If this type of spillover from interstate trade is widespread nationally, then the economy-wide jobs effect of the ARRA may be actually larger than what we find.The only question that one would ask in this context is this: If you knew your results were incapable of saying anything about the macroeconomic effects of the fiscal stimulus package why provide to the public debate partial estimates only and purport them to be saying something important about the “the causal effect on employment of the government spending component of the ARRA”. That question would remain even if their reported results said more than nothing. Conclusion Econometrics is an inexact art. But there are conventions and norms employed by practitioners such as myself in an effort to take the “con” out of econometrics. Conley and Dupor have bent the rules to make their point. Presumably they want to add to the conservative groundswell against the fiscal intervention. They could have done a better job. As it stands the paper says nothing of interest and cannot be used as an authority by those who wish to discredit the fiscal stimulus. That is enough for today!]]>
Thanks. A very fine and accessible analysis. Me thinks it is obvious why the authors choose a level of significance of 0.1 By doing so they maximize their professional utility. The paper – or better only the abstract – is already all over the place. Most people won’t bother to further scrutinize their “findings”. Mankiw starts his advertising machine. Mission accomplished. 15 minutes of fame for some obscure guys.
Good discussion.
But I was a bit confused at times, you write: “In my experience, 5 per cent is the norm for my profession. A level of significance of 10 per cent is considered too large because it creates too wide an interval”
Wouldn’t the 5 percent significance produce a wider, not narrower, confidence interval? At 95% the range could be from -4 to +3 million jobs, instead of -2.7 to +1.5 : we gain confidence at the price of precision (if we want 100% confidence we lose all the precision: the interval is -infinity to +infinity with 100% confidence).
It is true that 95% confidence would make the result look much less credible, and consistent with total lack of dependence: jobs vs stimulus, so your diagnosis stands, I was just confused at wording, but maybe I am not used to the jargon.
@ Peter
“Wouldn’t the 5 percent significance produce a wider, not narrower, confidence interval?”
I’m treading in deep water here — but I think that you’ve misunderstood.
From what I can see Bill is saying that a 5% significance would produce a result that is MORE accurate — not less, as you seem to suggest (if I’ve understood you correctly). The trade-off being that it has more chance of excluding a possibly true result.
This leads Bill to point out that if the authors are using a larger percentage point significance than they usually do (in this case 10%), they may well be allowing their analysis to be less accurate because they are trying to allow for a more ‘ominous’ outcome. To put it in more colloquial language, they’re casting a wider net and this leads them to take in more range — at the expense of accuracy.
This leads Bill to write:
“If we go back to the hypothesis testing angle – the higher the level of significance the easier it is to accept the null hypothesis that the point estimate is what it is. So if you are really bent on “proving” something then the higher the significance level the more likely you will find the coefficient estimates “statistically significant”. That is why professionals like me get suspicious when you see someone use the 10 per cent level – which is not the industry norm.”
You see when he says “the higher the level of significance the easier it is to accept the null hypothesis”? In my understanding that means that because the authors use a 10% rather than a 5% level of significance they are more likely to accept a dodgy conclusion (“null hypothesis”). So, they have given up on accuracy in favour of a more ‘generalised’ result. Bill asks why they do this — it’s a good question.
At least, that’s what I’ve taken from the post — but I’m not econometrician… not by a long shot. Hell, I can barely get the ‘anti-spam math answer’ correct half the time!
I can only assume that the authors used a 10 percent level because their results would not meet the 5 percent standard. This reflects very bad on them, because I’ve always been told that the 5 percent level is the norm in the social sciences. Forgive me if things are different in the econometric world, but my basic statistics class taught me that the results of a number of statistical tests like chi-square, simple regression, multiple regression, etc. have to meet a certain level to be considered statistically significant. Like I said, in the social sciences it is usually 5 percent. If the test statistic is less than 0.05 then we can say that the results are statistically significant (there is a relationship between the variables) and we reject the null hypothesis (the null hypothesis is that the variables are NOT related). This means that there is only a 5 percent chance that we have erroneously rejected the null hypothesis. An answer at the 10 percent level means there is a 1 chance in 10 that the null hypothesis was rejected in error. So the only reason to use a 10 percent level is because their results are not up to the standard which is normally used in the social sciences.
But maybe econometrics is completely different!
Peter and Philip,
Because the estimated coefficient is based on observations of a random variable, it will have a sampling distribution. If you take a different sample, you will end up with a different estimate. In other words, in general, the estimate does not equal the true population coefficient. The significance level is the probability that you end up with the estimate at least as extreme as the one that you’ve ended up with, taking the null hypothesis as a given.
E.g., imagine that the null is that there is no relationship between two variables x and y, and that you think true or population model can be described by a linear regression model like y = a + bx + u, where u is an error term. Call the estimate of b that you derive from your sample b*. What are the odds that b* does not equal zero even though, according to the null, b equals zero? That’s what significance levels tell you. A result that is significant at the 5% level means that in repeated samples, 5% of the time or less you will end up with a non-zero coefficient even though the true coefficient is zero. The lower this level, then, the lower the chance you have of falsely rejecting the null.
Vimothy,
5% and 10% do not refer to probability that b is not equal zero, they are probabilities that the true parameter lies outside the confidence interval. That is why the 95% confidence (significance 0.05) is a WIDER interval, not narrower: if you want larger prob that your range contains the true parameter (95% vs 90%), you gotta widen the range.
Peter,
Say that Y~Normal(μ,1) and that {Y_1,…,Y_n} is a random sample from the population. The sample average, Y ̅, has a normal distribution with mean µ and variance 1/n. We can take the sample outcome of the average, y ̅, and construct a 95% confidence interval for µ as follows,
It’s also important to note that the correct interpretation of the interval estimate is not “the probability that µ is in the above interval is 0.95”. It is that, in 95% of repeated samples, the constructed interval estimate will contain µ.
This has nothing to do with significance levels per se. Significance levels relate to hypothesis testing, i.e. statistical inference. They arise when we are interested in the answer to specific questions. For example, is a particular coefficient greater than zero? The significance level of a test is the probability of committing a Type I error. Denoting the level as α, formally we define it as,
Or, the probability of rejecting H_0 given that H_0 is true. We can test a variety of nulls using different statistical tests. We aren’t limited to only testing whether a particular individual coefficient is different from zero.
“The lower the level of significance the higher the probability that the estimate will lie within the interval but also the interval becomes narrower.”
I was confused for the same reason as Peter. It would be great if the width of the interval got narrower as you lowered the level of significance – your precision would increase with your confidence in the accuracy of the statistic! The problem with this paper was that even after *increasing* the level of significance to 10%, the interval was still so wide that it spanned zero. So it tells you precisely nothing.
But I don’t know, maybe economists use different confidence intervals to biologists.
Vimothy: You say: This has nothing to do with significance levels per se
It has a lot to do. If I take 10% significance level, my conf interval is [y ̅-1.64/√n,y ̅+1.64/√n]. it is a NARROWER interval, not wider, do you agree? I will reject or accept depending if b=0 is in this interval.
Haha – posted without seeing vimothy’s last comment, I may be talking bollocks!
If you specify a 10% significance level, it just means that your tolerance for Type I error is higher than in the alternate case with a 5% level. It doesn’t affect the computation of a 95% confidence interval at all.
Vimothy,
So what confidence interval are you using for the hypothesis testing with 10% significance level? I think that you are using the [y ̅-1.64/√n,y ̅+1.64/√n] interval.
If I was using the CI to carry out the test, then yeah.
Maybe I was missing your point above.
In fact, I agree with you:
“Wouldn’t the 5 percent significance produce a wider, not narrower, confidence interval”
Sorry, revising at the moment and seemingly can’t think write or read straight!
Dear Bill,
I managed to skim through 60% of the paper and I have enough. I have skipped the statistics not because I can’t understand it (I can if I have to but I am not going to waste my time tonight).
The main issue is much more fundamental. They see certain correlations between the numbers of jobs lost in the private sector (services and manufacturing) , these gained in the public sector and the (net) size of the stimulus. Then on that basis they try to prove the thesis that the stimulus has caused the job loss.
This is what forms the central axis of the argument:
“Figure 5: Growth in HELP services employment versus ARRA outlays net of budget loss, by state.
corr = −0.35”
So there is negative correlation between the size of the assistance minus budget loss and the growth of employment in the private services sector.
They use the following formulae to estimate job losses:
EM P LOY = a × (OF F SET − LOSS) + c × AN C + e (without fungibility)
and
EM P LOY = b × OF F SET − d × LOSS + k × AN C + e (with fungibility)
“The corresponding elasticity for the HELP service sector is negative -0.096.” (Fungibility restriction imposed) or -0.109 (without that restriction)
see Table 5.
The meaning of the first statement in the context of the paper is that 1% of increase in ARRA outlays relative to the state’s pre-recession revenue results in employment in the HELP sector that is 9.6% lower in September 2010.
This is exactly what is wrong – not the low confidence levels in the estimated coefficients but that element. “Correlation does not imply causation.”
I will illustrate that point.
Let’s imagine that high positive correlation has been established between smoking and lung cancer. The behaviour of the humans can be best explained using the rational expectations hypothesis. Everyone knows what is going to happen in the future and acts in a rational way in order to maximise the integral of his/her utility function over time.
These who know that they will die because of the cancer, choose to smoke in order to help their lungs to deal with the disease. Knowing the correlation determined by the statistical study we have proven that lung cancer expectations cause smoking.