Investment and profits

I am now using Friday’s blog space to provide draft versions of the Modern Monetary Theory textbook that I am writing with my colleague and friend Randy Wray. We expect to complete the text by the end of this year. Comments are always welcome. Remember this is a textbook aimed at undergraduate students and so the writing will be different from my usual blog free-for-all. Note also that the text I post is just the work I am doing by way of the first draft so the material posted will not represent the complete text. Further it will change once the two of us have edited it.

The role of Investment in Profit Generation

1. Investment in a Capitalist Monetary Economy

In Chapter 5 National Income and Product Accounts, we learned that investment spending – or Gross fixed capital expenditure – is a major component of aggregate demand. In Chapter 6 Sectoral Accounting, we noted that investment formed one row in the Transactions matrix as did the term Profits.

In this Chapter, we tie those two aspects of business activity together.

Profits and investment spending are intrinsically linked in a Capitalist economy, which we described in Chapter 2. In this Chapter we examine the behaviour of private investment spending and seek to explain where profits come from in a macroeconomic sense.

We prioritise a study of investment for three main reasons.

• It fluctuations help to account for the business cycle. Movements in economic activity and hence employment are strongly driven by fluctuations in private investment. The other main components of aggregate demand being relatively stable.
• Investment spending is an important determinant of total profits in the economy.
• Investment spending can be significantly altered by government policy, which means that policy can “manage” the economic cycle somewhat through its influence on private investment growth.

Economists use the term investment differently to the common usage, which might include people placing their saving in the form of financial assets, real estate and other speculative vehicles.

In the financial papers and reports you will often read or hear, for example, that “investors have become more pessimistic” in relation to bond prices or other financial assets. Use of the term “investors” in this context if different to the way we use it in macroeconomics.

Investment is defined in macroeconomics to be that spending which is devoted to increasing or maintaining the stock of productive capital.

The capital stock is comprised of factories, machines, offices, and other durable products that are used up in the production process, inventories and residential housing.

Investment spending is a flow of expenditure which adds to the stock of productive capital.

The Volatility of Investment

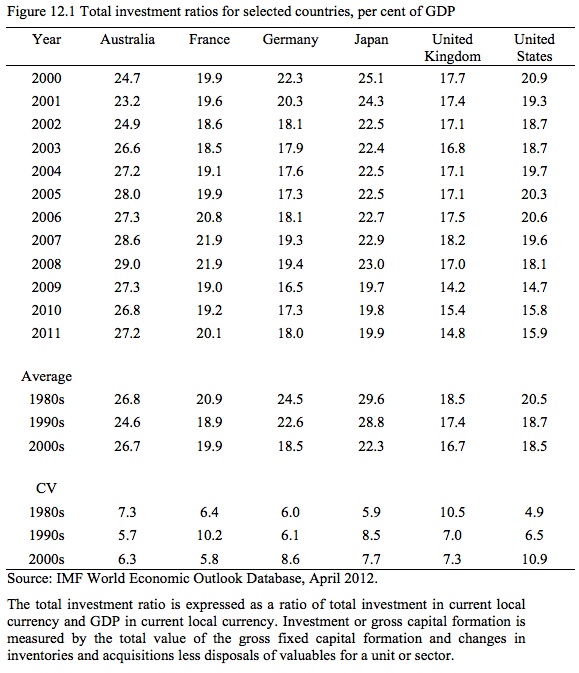
Figure 12.1 shows Total Investment ratios for selected countries from 2000 with decade averages provided for the 1980s, 1990s and 2000s. CV is the coefficient of variation which is defined as the ratio of the standard deviation to the mean and provides what statisticians call a normalised measure of dispersion. The coefficient of variation allows one to compare dispersion across very different samples without recourse to information about the underlying average.

Except for Australia, the investment ratios have been falling. For Germany, Japan and the United States, the investment ratio has also become more volatile.

Gross and Net Investment

Gross Investment is defined as the total addition to the existing capital stock. However, in any given period, some of the existing capital will become inoperative due to wear and tear and have to be replaced. This component of spending is termed depreciation.

Net Investment subtracts depreciation from Gross Investment. Depreciation is the reduction in the capital stock that occurs each period through wear and tear.

Thus net investment is the increase in the capital stock per period. In any given period, net investment could be negative. If firms decide they have too much capital given their expected sales then they will invest less than is necessary to maintain the size of the existing capital stock. Thus the depreciation will be larger than the gross investment which means net investment would be negative.

What determines the decision by firms to invest?

The most elementary explanation is based on the observation that business firms require stocks of capital on hand to produce output. In this context, they have to consider two broad aspects of the production decision:

• 1. Will the size and composition of the capital stock in place allow them to produce at the lowest cost?
• 2. Is the capital stock adequate to produce the expected output in the coming periods?

The analysis that business firms engage in to answer these questions then determines their investment decision.

Investment attempts to bridge the gap between the current capital stock and the desired capital stock based on their analysis of future expected output. Investment will be high when the current capital stock is low relative to expected needs. Conversely, investment will be low when the current capital stock is high relative to expected needs.

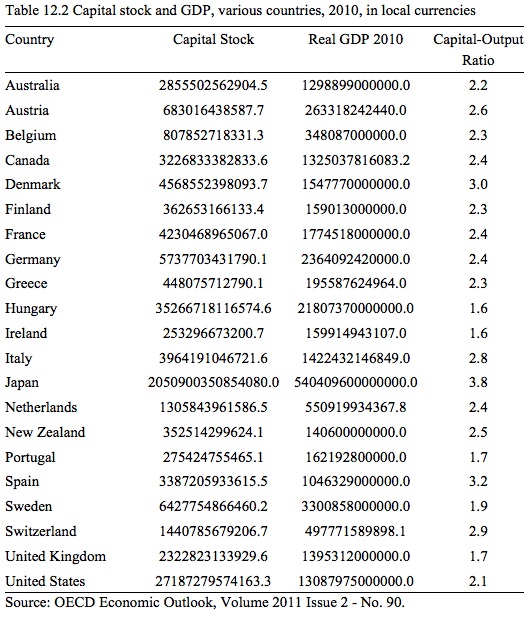
Given that capital goods last for many years, the capital stock will typically be large relative to current national income (GDP) and current investment (I). Figure 12.2 compares the estimated capital stock and GDP for various countries in 2010. The average capital stock for the OECD nations shown for 2010 was 2.4.

[NOTE – THIS TABLE IS TO BE REVISED]

If business firms maintain these typical ratios then small changes in GDP will lead to large changes in the amount of capital goods required. So when the change in GDP (ΔY) triggers the desire to change the capital stock, large fluctuations in investment usually occur.

This observation is the basis of the Accelerator model of investment.

The Accelerator model of Investment

The Accelerator model of investment is based on the observation that increases in GDP lead to increases in the desired stock of capital (denoted K*).

The desired stock of capital (K*) is the amount of capital that business firms would like to have in place given the current and expected economic conditions. As a result of the capital stock (K) being carried over from the previous period and increase in GDP which leads to an increase in K* will lead to a discrepancy or gap between the actual capital stock in place and K*.

Investment behaviour is characterised as the attempt by the business firms to close this gap. The accelerator terminology is based on the fact that small changes in GDP will drive larger or accelerated changes in investment demand (spending).

Simple accelerator model

With a given production technology (that is, state of art) we consider the capital to output ratio (K/Y) to be fixed. This means that it takes a fixed collection of capital (K) to produce a given output level (Y

We use this simple assumption to define the desired capital stock (K*) as:

(12.4) K* = vY

Where the fixed multiple, v is the desired capital to output ratio (K/Y). This means that to produce Y firms have to have K/v in place.

For example, if the capital to output ratio was 2 and output was expected to increase by $10 billion then firms would revise their desired capital stock upwards by $20 billion to ensure they had enough productive capacity in place to meet the expected increase in demand for goods and services.

In order to increase the capital stock to meet the change in desired capital stock, firms will invest. While this model of investment is too simple and we will complicate it further later in the Chapter, it does provide some essential and useful insights that describe investment behaviour in most economies.

These insights are:

• Investment demand will be much more variable than GDP because investment is a multiple of the change in income (GDP).
• In an actual economy, investment starts to decline before an economy goes into recession. In other words, we can use turning points in the flow of investment spending to make predictions about the direction of the business cycle. It is clear that when GDP is rising in the early stages of a recovery, then the change in income will be positive and investment will be high. But as the growth in GDP tapers off, the change in income decreases which means that investment starts to decline even though the level of GDP may still be rising.

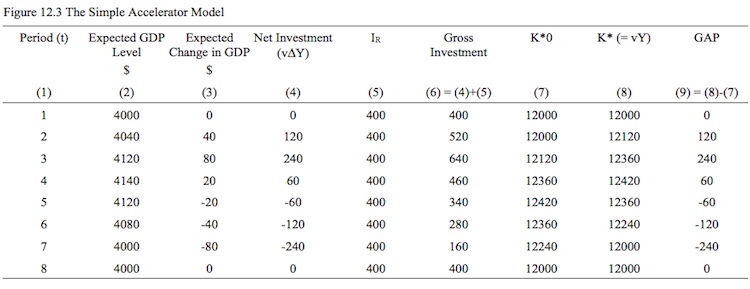
A practical example will help you understand how this model works. Assume that the accelerator coefficient (v) is equal to 3 and replacement investment is a constant $400 per period. Assume the economy has an initial capital stock of $12,000.

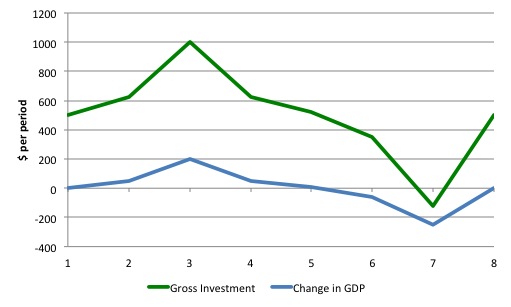
Figure 12.3 shows the Simple Accelerator Model of investment spending in action for 8 hypothetical periods where income initially grows from $4,000 to a peak of $4140 then declines back to $4000.

You might like to create a spreadsheet yourselves to replicate the table and then start varying the key inputs (expected aggregate demand, the capital-output ratio) to see what happens to investment.

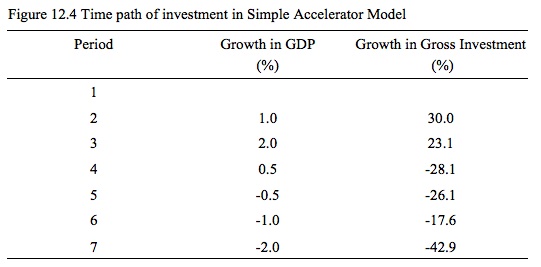
Figure 12.4 shows the time path of investment spending described in Figure 12.3? You can observe that fluctuations in GDP growth drive much larger fluctuations in investment spending growth.

Figure 12.5 captures the relationship between the change in GDP and Gross Investment. The increased variability of investment for a given change in GDP is very stark.

Figure 12.5 Relationship between change in GDP and Gross Investment, Simple Accelerator Model

Limitations of Simple Accelerator Model

While the Simple Accelerator Model is a useful guide it is too simplistic for the following reasons:

• The desired capital stock K* is unlikely to remain a fixed proportion of GDP. That is, the accelerator coefficient v is likely to be variable in the real world.
• Following a change in GDP, business firms to not attempt to close the gap between their actual and desired capital stocks immediately. That is, like most adjustment process in the real world, adjustment takes place gradually over time.

These observations led economists to develop the Flexible Accelerator Model, which adds some complexity to the explanation of investment.

The Flexible Accelerator Model

This model of investment behaviour assumes that for a time, business firms can continue to function adequately with a capital stock that is not exactly equal to its desired capital stock.

There are several reasons why firms might want to adjust gradually to their desired capital stock:

• Adjusting the capital stock is very costly especially as suppliers usually charge premiums for faster delivery.
• There are intrinsic time lags involved. It take time to undertake project evaluation to consider the type of capital, the likely suppliers, the financing arrangements, the delivery details and the installation and training associated with the new equipment.

For these reasons, while investment is motivated to closing the gap between the actual capital stock and the desired capital stock (K* – K), there is incomplete adjustment in the short-run.

Business firms employ alternative strategies to maintain operations and production with a less than desired capital stock. These include running extra shifts – that is, spreading more labour resources over the existing capital stock; providing opportunities for over-time and extended working weeks.

The Flexible Accelerator Model thus conceives that business firms adjust to increased output by employing a combination of more labour and some investment which augments the capital stock. Over time, they catch up with their desired K*, although in a growing economy, they are always likely to fall short, given the incomplete adjustment process conceived here.

Rate of Adjustment in Flexible Accelerator Model

The additional question that then arises is what is the speed of adjustment (which we might denote as d)?

The rate of adjustment (d) is the fraction or proportion of the gap (K* – K) that is closed by the flow of investment per period. If the gap is mostly closed (that is, firms get close to their desired capital stock quickly) then d will be large and we consider the rate of adjustment to be fact. The speed of adjustment is slow is the gap persists over a long period.

What does the rate of adjustment depend upon? There are several determinants that economists have identified:

• Adjustment costs – the costs of financing (for example, determined by the interest rate).
• Time factors – how long does it take for new capital equipment to be evaluated, designed, ordered, produced, delivered and installed.
• Economic conditions – interest rates, expected returns on production, animal spirits (business sentiment).

We might say that the higher the interest rates the higher the costs of financing capital equipment purchases (other things being equal) and so the slower the adjustment will be.

Further, bouts of pessimism will slow down adjustment. We will return to this issue later in the Chapter when we consider the asymmetric nature of investment demand.

We will return to the impact of higher interest rates presently.

Implications of incomplete adjustment

By comparison with the Simple Accelerator Model, if in each period the adjustment to the desired capital stock is less than 100 per cent then the gap between K* and K will remain non-zero. That is, the actual capital stock will not equal the desired capital stock.

In the Flexible Accelerator Model, the flow of investment demand (spending) is dependent not only on the gap between K* and K but also the speed of adjustment.

What affect does this have on investment spending?

The partial adjustment smooths out the impact of a change in GDP on the flow of investment demand over several periods. Thus sustains investment even when output growth falls.

The Simple Accelerator Model posited what we might term an explosion-contraction pattern of investment demand which is clearly unrealistic. The Flexible Accelerator Model predicts a smoother investment path but still highly variable.

Consider the case of a growing economy. Investment spending will be positive because the actual capital stock is below the desired capital stock (K*). Business firms use investment to adjust towards their desired capital stock. So investment demand depends on two factors:

• The amount needed to replace the capital that has been worn out (depreciation), I_R.
• The positive or negative amount necessary to adjust for the change in GDP.

[NOTE = A TABLE AND GRAPH COMPARING THE SAM AND THE FAM TO COME HERE]

Expectations and Interest rate impacts on investment demand.

We saw in the discussion of the Flexible Accelerator Model of investment demand that economic conditions have an impact on the estimates of desired capital stock by business firms.

Two factors were identified as being important:

• Expectations of future economic conditions.
• The interest rate

Business firms are continually forming expectations about future output. Firms have to make resource commitments (working capital, labour etc) well in advance of realisation (sales) and so the scale of production at any point in time reflects the guesses they make in a highly uncertain world.

The extent to which investment demand follows the Flexibile Accelerator model of capital stock adjustment depends on these expectations.

Managers wonder whether a change in output that they observe in the current period will be sustained or not. They consider whether observed changes in output are the result of transitory (ephemeral) factors or a likely to be enduring. The wonder whether a rise in demand (output) today might not be followed by a fall tomorrow.

The Flexible Accelerator Model of investment is called a partial adjustment model (PAM) and the lack of complete adjustment to the desired capital stock reflects, in part, the uncertainty about the duration of the change in income.

When output is unusually high, business firms might form the view that it will taper off and so they will allow the current capital stock to depreciate more than usual (that is, net investment will be negative).

Alternatively, when they consider output levels to be unusually low, a reasonable expectation is that it will rise and so firms overinvest in the short-run to ensure they have enough capital in place to meet their expected future demand. In other words, they create productive capacity that is beyond their immediate requirements.

What about the interest rate?

[NOTE DISCUSSION HERE ABOUT KEYNES and MARGINAL EFFICIENCY OF CAPITAL ETC]

Cyclical Asymmetries in Investment Spending

Another aspect of investment behaviour that we observe in the real world is asymmetry. Investment in new capital stock usually requires firms to make large irreversible capital outlays.

Capital is not a piece of putty that can be remoulded in whatever configuration that might be appropriate (that is, different types of machines and equipment). Once the firm has made a large-scale investment in a new technology they will be stuck with it for some period.

In an environment of endemic uncertainty, firms become cautious in times of pessimism and employ broad safety margins when deciding how much investment they will spend.

Accordingly, they form expectations of future profitability by considering the current capacity utilisation rate against their normal usage.

They will only invest when capacity utilisation, exceeds its normal level. So investment varies with capacity utilisation within bounds and therefore productive capacity grows at rate which is bounded from below and above.

The asymmetric investment behaviour thus generates asymmetries in capacity growth because productive capacity only grows when there is a shortage of capacity.

This insight has major implications for the way in which economies recover and the necessity for strong fiscal support when a deep recession is encountered. We will consider these issues in Chapter 13 Government and Fiscal Policy.

Investment and Profits

What is the relationship between investment spending and the profits that a firm receives? The origin of profits has been an on-going debate among economists since Capitalism succeeded Feudal modes of production.

[NOTE DISCUSSION OF MARX AND SURPLUS VALUE AS THE ORIGIN OF PROFITS]

In this section we consider the theory of profits that was developed by Polish economist, Michal Kalecki, who was one of the early pioneers in developing an understanding of the origins of profits from a macroeconomic perspective.

There were two versions of Kalecki’s theory – a simplified version which outlined the fundamental profits equation and the more realistic expanded version which outlined the generalised profits equation.

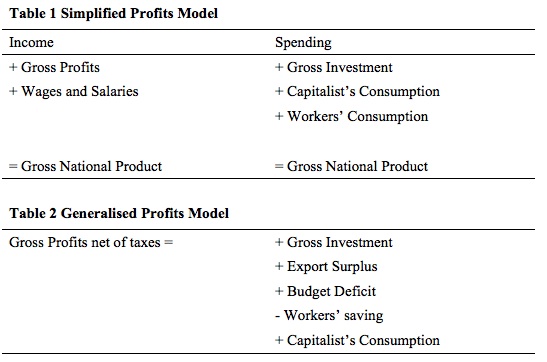
Figure 12.6 shows the tables that were originally published in Kalecki’s 1952 book – Theory of Economic Dynamics – which was republished in 1965 by Allen and Unwin, London.

The tables show the simplified and generalised versions of the Kalecki’s profits equations.

Figure 12.6 Kalecki’s Simplified and Generalised Profits equations

Kalecki was trained under a Marxist system and so had an advanced understanding of how the production of surplus value pre-dated but determined profit realisation. The mainstream idea that profits were generated in the “exchange” process (where goods and services are bought and sold) and reflected the marginal contribution of capital was dismissed.

[NOTE – brief section here differentiating Kalecki’s effective demand emphasis from Marx’s surplus value focus]

What Marx didn’t show in his approach to profits was how the total volume of profits in a monetary economy was determined in any given period. That was the question that Kalecki sought to answer.

When students first confront the question of the determination of profits from a macroeconomics view they have trouble reconciling it with the more normal approach to accounting at the firm level.

As we have learned in earlier chapters it is easy to fall into the trap of the fallacy of composition where we apply what we observe at the individual level to the macroeconomic level. In this case, attempting to formulate a macroeconomic theory of profits by applying the logic that an individual firm might apply to calculate their profits will lead us astray.

Think about this example. Wage costs are a significant proportion of total costs at the firm level. So if an individual firm was to achieve significant reductions in its wage costs, then it might expect to enjoy increased profits.

Imagine if all firms simultaneously attempted the same strategy. What would you expect to happen?

Given wage costs are also worker incomes and as we have learned spending is driven by income, we would expect the total revenue for firms to decline as they cut wage costs. There is no reason to expect that overall profits would rise in the economy.

Further, investment may also decline as total spending declines, which would further damage the revenue side of the business sector.

The first task then is to determine what factors are important for creating the overall level of profits in the economy.

Kalecki’s simplified model

In his simplified model, Kalecki assumed that the economy was comprised of two groups:

• Workers who earned wages and did not save; and
• Capitalists who produced and earned profits.

He also assumed that the economy was closed and that there was no government sector.

Under these highly simplistic assumptions, Kalecki concluded that “workers spend what they get” and “capitalists get what they spend” which means that capitalist profits are determined by their own propensity to invest and consume which reverses the way people normally consider the causation.

That is, profits are determined by investment not the other way around.

While Kalecki clearly knew that workers also save, he was able to show that by adopting the restrictive “workers do not save” assumption the basic insights were not altered but rendered more easy to understand.

To reach that conclusion, Kalecki began with the familiar National Accounting identity, which we developed in full in Chapter 8. In his simplified model, the basic aggregate demand equation is written as:

(12.5) GNP = C + I

Where GNP is Gross National Product or total output and national income, C is total private (household) consumption, and I is total private investment spending per period. These aggregates are all flows of expenditure (and hence income).

Note he used GNP rather than Gross Domestic Product (GDP) because he assumed the economy was closed. Refer back to Chapter 5 National Income and Product Accounts if you need to refresh your memories of the difference between these two aggregates.

Private investment is the sum of spending (output) of new productive capital plus changes in inventories.

In terms of analysing how the total income produced was distributed, Kalecki assumed that there were two “classes” – workers and capitalists – which shared the national income such that total wages and salaries (V) plus total profits (P) equals GNP.

Kalecki expressed the distribution of national income in this way:

(12.6) GNP = V + P

P is gross profits which includes depreciation, retained profits, dividends, drawings from unincorporated firms, rent and interest.

Equation (12.5) describes the national product from the spending (demand) side, while Equation (12.6) considers the same aggregate from the perspective of how it is distributed.

If we set the two different views of the National Accounts equal we get:

(12.7) V + P = C + I

Or:

(12.8) P = C + I – V

Note that (C – V) is that component of consumption that is attributed to the capitalists (given workers’ consumption is equal to V – that is, they “spend what they get”).

Equation (12.8) can be read as saying that gross profits (P) is equal to capitalists’ consumption (C-V) plus gross investment. That is, the capitalists “get what they spend”.

This is the model presented in the first segment (Table 1) es in Figure 12.6.

Clearly, the simplified (fundamental) profits equation was derived from the national accounts and so is true by definition. Kalecki sought to expand his analysis further by explaining the causal dynamics that led to the existence of profits overall (at the macroeconomic level) – which linked the two sides of the fundamental equation.

The question of interest is which way the causality flows – from left to right – Do profits determine capitalist consumption and investment? – which is the intuitive way of thinking – or from right to left – Do capitalist consumption and investment determine profits? Kalecki clearly considered the latter causality to be the valid way of understanding profits.

He said (in his 1965 book Theory of Economic Dynamics, pages 45-46):

The answer to this question depends on which of these items is directly subject to the decisions of capitalists. Now, it is clear that capitalists may decide to consume and to invest more in a given period than in the preceding one, but they cannot decide to earn more. It is, therefore, their investment and consumption decisions which determine profits, and not vice versa.

He recognised that there was a time-lag involved between spending and profits. It is the recognition of this time lag that allowed Kalecki to derive his business cycle model, which we consider later in this Chapter.

The essential insight is that investment spending depends on expectations of future aggregate demand that are formed in some prior period.

These spending decisions then drive economic activity and so profits are a function of investment in some prior period and these flows can be variable.

In effect, he foresaw an accelerator type process operating. Later in the Chapter we will consider how the accelerator interacts with the expenditure multiplier, which we derived in Chapter 8, as part of a broader explanation of business cycles.

It is clear that in the simplified profits model – capitalist’s gross saving equals gross investment. Kalecki (like Keynes) demonstrated that the equality of saving and investment was totally independent of the level of interest rates which were determined in the money market. But remember the simplified model assumes only two sectors – households and firms.

The neoclassical approach considered interest rates adjusted to equilibrate (real) saving and investment and thus ensure that aggregate demand would always be equal to aggregate supply – thus negating the possibility that the economy could suffer from a shortage of demand. This denial of unemployment was the basis of Say’s Law (later Walras’ Law).

However, Keynes and Kalecki clearly understood that saving and investment were brought into equilibrium (in a closed economy without a government sector) by variations in national income driven by changes in effective (aggregate) demand. That insight provided the fundamental break with neoclassical thinking that dominated economics (and policy) at the onset of the Great Depression and which, when applied, worsened the depression.

So in Kalecki’s model, fluctuations in spending drive fluctuations in output and income which ensure the demand drain (saving) comes into equality with spending injections (investment).

This is also the basic idea that drives the spending multiplier model. Thus increased investment spending stimulates aggregate demand and firms respond by increasing production.

This, in turn, leads to higher wage and salary payments and higher induced consumption which feeds back into the spending stream and promotes further output and income. At each stage of the process, some of the income generated goes to saving and so the successive consumption spending flows become smaller and smaller until they exhaust. At that point, the sum of the saving generated by the income responses will equal the initial investment injection and the economy regains equilibrium.

A person thinking from a micro perspective might think the profits equation is odd – after all, if the capitalist consumes more the volume of funds they have at the end of some period should be less. It is here that the fallacy of composition enters the fray.

Kalecki asked “what would be the sources of financing this investment if capitalists do not simultaneously reduce their consumption and release some spending power for investment activity?” He responded as such (in his 1966 book – Studies in the Theory of the Business Cycle (Blackwell, Oxford), page 46):

It may sound paradoxical, but according to the above, investment is ‘financed by itself’.

While that might be true for an individual business firm, acting in isolation, it cannot be true for the economy as a whole. This is because the consumption of one capitalist becomes the source of profits for another capitalist. This insight allows us to understand the statement that capitalist investment brings forth its own saving!

Kalecki clearly understood that counter-intuitive notion that investment “automatically furnishes the savings required to finance it” as long as their is idle capacity. That is, as long as increasing aggregate demand does not outstrip the real capacity of the economy to produce.

Kalecki’s Generalised Model of Profits

[NOTE: next time]

Saturday Quiz

The Saturday Quiz will be back again tomorrow. It will be of an appropriate order of difficulty (-:

That is enough for today!

(c) Copyright 2012 Bill Mitchell. All Rights Reserved.