It’s Wednesday and I just finished a ‘Conversation’ with the Economics Society of Australia, where I talked about Modern Monetary Theory (MMT) and its application to current policy issues. Some of the questions were excellent and challenging to answer, which is the best way. You can view an edited version of the discussion below and…
Introducing economic dynamics
I am now using Friday’s blog space to provide draft versions of the Modern Monetary Theory textbook that I am writing with my colleague and friend Randy Wray. We expect to complete the text by the end of this year. Comments are always welcome. Remember this is a textbook aimed at undergraduate students and so the writing will be different from my usual blog free-for-all. Note also that the text I post is just the work I am doing by way of the first draft so the material posted will not represent the complete text. Further it will change once the two of us have edited it.
The material today continues the derivation and significance of Michel Kalecki’s theory of profits and then considers the issue of economic fluctuations. The consideration of economic dynamics brings together the concept of the expenditure multiplier which demonstrated how an injection of spending into the economy would, if there was excess capacity, multiply as the extra income generated was re-spent, and the accelerator model of investment spending, which was introduced earlier in this chapter.
Kalecki’s Generalised Model of Profits
Kalecki subsequently complicated his simplified two-sector model to include a foreign sector, a government sector and a recognition that workers do save. He considered this generalised theory to be applicable to the real world.
He sought to sought to examine the influence of the budget deficit, the external sector and workers’ savings on total profits.
In Chapter 8 we introduced the real expenditure model of national income determination and derived the aggregate demand equation as:
(12.9) Y = C + I + G + NX
where Y is national income (aggregate spending), G is government spending and NX is net exports (total exports minus total imports). In Kalecki’s model where workers and profit recipients were distinguished, C is taken now to be the aggregate of capitalists’ consumption (Cp) and workers’ consumption. Workers’ consumption is equal to total worker income post tax (Vn) minus workers’ saving (Sw).
To recognise the different sources of total consumption, Equation (12.9) could thus be written as:
(12.10) Y = Cp + (Vn – Sw) + I + G + NX
Total income claimants on national income (Y) are:
(12.11) Y = Pn + Vn + T
where P and V are as before (profits and total wages and salaries) but the subscript n denotes these flows are net of taxes paid, and T is total taxes.
Thus (setting the expenditure components of total income equal to the claims on total income) we get:
(12.12) Cp + (Vn – Sw) + I + G + NX = Pn + Vn + T
We can solve this for Gross Profits after tax (Pn) to get:
(12.13) Pn = I + (G – T) + NX + Cp + Vn – Sw – Vn
So:
(12.14) Pn = I + (G – T) + NX + Cp – Sw
which says that gross profits after tax (Pn) equals gross investment (I), plus the budget deficit (G – T), plus the export surplus (NX), plus capitalists’ consumption (Cp) minus workers’ saving (Sw).
This is the model shown in Figure 12.6 as Table 2.
Gross profits after tax will be higher, the higher is gross investment (I), the larger the budget deficit (G – T), the higher is capitalists’ consumption (Cp) and the lower is workers’ saving (Sw).
[NOTE: A SECTION ON THE BEHAVIOURAL FACTORS THAT INFLUENCE Cp and Sw TO BE INSERTED HERE]
Kalecki identified some interesting features of this model.
For example, when there are positive net exports and/or budget deficits, then gross net profits (Pn) will rise higher than the level that would be generated by gross investment and capitalist consumption (as in the simplified model).
So an individual domestic capitalist who is able to increase their net exports will be able to glean extra profits “at the expense of their foreign rivals” [NOTE: GET EXACT QUOTE FROM Kalecki, 1964:51).
Kalecki said (in his 1965 book noted above, page 51):
It is from this point of view that the fight for foreign markets may be viewed.
[NOTE – A FURTHER ELABORATION OF THE FOREIGN SECTOR WILL APPEAR IN CHAPTER 15 THE OPEN ECONOMY]
Anticipating the discussion of fiscal policy in Chapter 13, Kalecki’s generalised model of the determination of aggregate profits considered budget deficits added to capitalist profits through their positive effect on national income. The budget deficit leads to the private sector receiving more dollar flows from government spending than it is returning to the government via taxes. Budget deficits thus provide an increased capacity for capitalists to realise their production plans and sell output because they expand the total aggregate demand in the economy.
Kalecki said that budget deficits allow the capitalists to make profits (net exports constant) over and above what their own spending will generate.
Government spending not only directly stimulates aggregate demand but through the multiplier effect it also increases the incomes of household, who, in turn, purchase goods and services from firms.
The opposite is the case. If the government runs a budget surplus – where spending is less than taxation revenue – then aggregate profits are reduced. There are two ways in which this occurs. Aggregate spending falls which reduces the revenue that firms receive. Further, if the surplus is achieved with increased business tax rates, then the firms have less after tax profit.
The only time that a rising budget deficit will not add to real profits is if there is full capacity and the rising deficits push nominal aggregate demand beyond the real capacity of the economy to increase output and real income.
A recurrent theme in the public debate which we will consider in Chapter 18 Policy Debates is the issue of crowding out. We also consider the concept of crowding out in Chapter 13 Fiscal Policy.
Basically, many economists think that government spending and private investment compete for a finite pool of saving and this competition has to be resolved by higher interest rates, which damages private investment.
Accordingly, budget deficits are said to “crowd out” private spending. The same economists typically add a further argument to justify their claim that budget deficits are damaging. They allege that public spending is generally wasteful in comparison to private spending because the latter is allegedly “disciplined” by the market. This is in reference to their belief that the self-regulating market results in the most efficient allocation of resources because inefficient uses of resources are priced out of use by demand and supply forces.
As a preliminary insight into why the crowding out argument is without substance, we can reflect on Kalecki’s profit determination model.
The crowding out argument relies on the claim that savings are finite and borrowers have to compete with each other to gain access to that finite pool.
Consider the conclusion that rising private saving (lower propensity to consume) and/or falling deficits impact negatively on profits. The impact is via declines in national income overall. It is probable that when firms are experiencing a reduction in profits as the conditions in the goods and services market deteriorate that they will reduce their rate of investment.
Equally, private investment adds to private profits and brings forth its own saving via the expansion of national income. In the same way, budget deficits add to private profits and, if accompanied by debt issuance, merely borrow back the funds they spend and stimulate growth in saving via the expansion of national income.
These are fundamental insights of a modern monetary economy that were well understood by Kalecki in his work on the determination of profits and the dynamics of a capitalist economy.
References
The key articles/books that outline Kalecki’s approach to profits are:
- Essai d’une theorie du mouvement cyclique des affaires, Revue d’economie politique, 1935.
- A Macrodynamic Theory of Business Cycles, Econometrica, 1935.
- Essays in the Theory of Economic Fluctuations, 1939.
- A Theory of Profits, Economic Journal , 1942.
- Studies in Economic Dynamics, 1943.
Business cycles – Fluctuations in Economic Activity
In the last section, we considered Michel Kalecki’s theory of aggregate profit determination. We gained an understanding of the way in which profits vary as national income fluctuates in response to variations in capitalist consumption and investment, workers’ saving, the budget balance and the external balance.
The fluctuations in economic activity and the resulting changes in national income are refered to as the business cycle. When economists refer to the business cycle they are considering fluctuations in economic activity that arise from variations in overall spending.
As a matter of terminology, economists often reference an economic variable in terms of the business cycle. There are three broad relationships:
- Counter-cyclical – which occur when a variable rises (falls) when the level of economic activity falls (rises). That is, we would observe a negative correlation between the variable and economic activity.
- Pro-cyclical – which occur when a variable rises (falls) when the level of economic activity rises (falls). That is, we would observe a positive correlation between the variable and economic activity.
- Acyclical – there is no relationship between the variable and economic activity. That is, there would be a zero correlation between the two variables.
Typical pro-cyclical variables are household consumption, business investment, imports and employment. Typical counter-cyclical variables are unemployment and underemployment, and the budget balance (we will explain this in more detail in Chapter 13 when we consider fiscal policy).
Economists also consider macroeconomic variables in terms of the timing of the business cycle. The points in time when the cycle moves expansion to contraction (the peak) or contraction to expansion (the trough) are referred to as turning points.
A variable that demonstrates cyclical behaviour before real GDP has “turned” is referred to as a leading indicator because its movement pre-dates the change in direction of the cycle.
Well-known leading indicators include new housing starts; new spending (orders) on plant and equipment by firms; purchase of consumer durables by households; and new job creation by firms.
Conversely, a variable that demonstrates cyclical behaviour after real GDP has “turned” is referred to as a lagging indicator because its movement post-dates the change in direction of the cycle.
Well-known lagging indicators include the rate of inflation; the change in persons employed; and the rate of wage inflation.
[NOTE A TABLE HERE SHOWING THE KEY MACROECONOMIC VARIABLES IN TERMS OF THEIR LAG/LEAD STATUS AND THEIR CYCLICALITY]
Figure 12.7 depicts a stylised business cycle detailing the essential elements that economists identify. These elements include the recovery or growth phase where real GDP is increasing period after period until it reaches the peak – the point at which real GDP reaches its localised maximum.
The economy then goes into a downturn of some severity – sometimes moderate and other times severe – where the real GDP declines overall. If this phase lasts for two or more successive quarters then the economy is said to be in recession. At some point the economy reaches the trough, which is the lowest point real GDP reaches of that particular cycle.
The trend real GDP growth rate depicts the underlying direction of real GDP by ignoring the cyclical fluctuations.
Note also that the real GDP growth can accelerate or decelerate while still remaining positive. For a recession to occur the level of real GDP has to decline (that is, negative growth must occur).
Figure 12.7 A Stylised Business Cycle
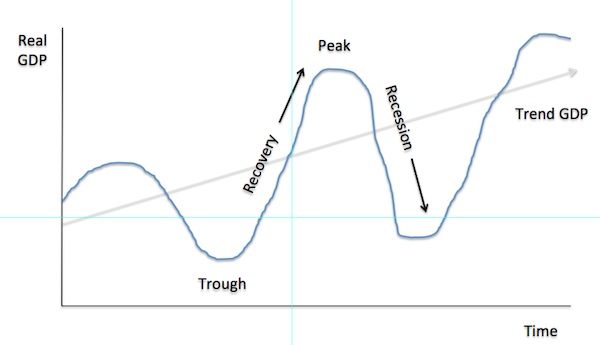
[NOTE: a more professional drawing will be inserted in the final textbook]
Figure 12.8 shows the evolution of annual percentage growth in real GDP for Australia from 1960 to the first-quarter 2012. The data is derived from the Australian National Accounts available from the Australian Bureau of Statistics and is quarterly in frequency. The formula used to calculate the annualised growth rate from quarterly data is as follows:
(12.15) Annual Growth = 100*(Real GDPt – Real GDPt-4)/Real GDPt-4
where the t subscript refers to the quarter in question. So if t was March 2012, then t-4 would be March 2011 and so on.
The graph depicts several business cycles over this period of different intensities. While each nation experiences different intensities of growth and contraction between peaks, the Australian experience is representative of the general pattern of economic development.
Figure 12.8 Australian real GDP growth, 1960-2012, per cent per annum
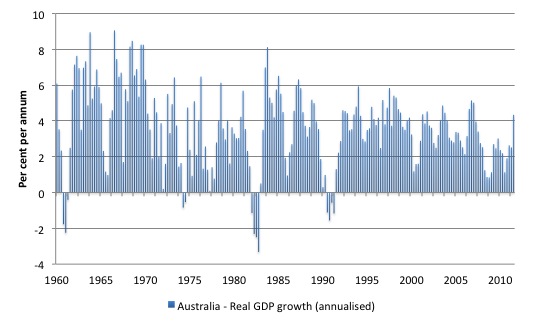
Source: Australian Bureau of Statistics, National Accounts data.
Economic fluctuations are not regular occurrences by which we mean the time span between peaks and troughs and the depth (amplitude) of the cycle are variable over time. While Figure 12.7 depicted peaks that increased over time it is possible to envisage a peak that falls below the previous peak.
The point to understand is that economic activity moves over time in these wave like patterns oscillating between peaks and trough as aggregate demand fluctuates.
We refer to a single business cycle as the time between two peaks because that period contains a completed upswing and downswing.
Other terminology has been used in relation to the business cycle. For example, economists sometimes differentiate between an recovery (upswing) and a boom in terms of the relationship to real GDP to its trend. So a recovery (from a trough) becomes a boom, once real GDP exceeds its current trend value.
Further, a downturn might describe the fall in real GDP between the peak and the trend line, whereas the economy might be considered to be in recession once real GDP moves below its current trend level.
A very deep and drawn out recession is sometimes referred to as a depression and, fortunately, governments have a good understanding of the policy tools at their disposable (fiscal and monetary policy) to ensure we rarely encounters recessions so harsh that we consider them to be depressions.
The Interaction of the Expenditure Multiplier and the Investment Accelerator
In Chapter 8, we introduced the concept of the expenditure multiplier which demonstrated how an injection of spending into the economy would, if there was excess capacity, multiply as the extra income generated was re-spent.
In this Chapter, we introduced the accelerator model of investment spending, whereby a firm would augment its capital stock through investment spending in order to have enough capital available to produce the expected demand for its output.
In this section we bring the two concepts together to show how a business cycle might evolve.
The material that follows is considered advanced and is based on the work by Roy Harrod [NOTE REFERENCE HERE]. The essential idea can be described in a relatively straightforward way.
The accelerator theory of investment spending is based on the notion that net investment is driven by expected changes in output demand. Firms thus seek to put in place capital stock which will be sufficient to produce the expected demand for their output at current technology and practice.
The multiplier concept indicates that when there is an exogenous boost in aggregate spending (for example, from government, investment and/or exports) the initial spending increase is multiplied through the expenditure system as consumers are induced by the rising income to increase their consumption.
The two concepts can thus interact. A multiplied spending increase and growth in output will, in turn, increase investment via the accelerator principle.
Given investment is a component of aggregate spending, the rise in net investment will, in turn, have a multiplied impact on total spending and output and so the economy moves into an upward phase in the business cycle.
But once the economy reaches a peak in real GDP, the accelerator becomes a negative influence on net investment which then via the multiplier generates a decline in total spending.
So there is an interaction between investment as an exogenous driver of the multiplier and investment as an induced spending reaction as a result of the accelerator principle.
This was the basic insight that underpinned the Harrod-Domar model of economic cycles (and growth) and supports the notion developed by Keynes that we considered in Chapters 10 and 11 on the labour market, that the economy has no natural full employment level that it gravitates towards.
In those chapters, we learned that because the capitalist economy is prone to under-full employment equilibrium positions which have to be disturbed by government policy stimulus.
|
Advanced Material
The Flexible Accelerator was defined as: (12.5) It = d[vYt – K*t-1] + IR If we only consider net investment we can ignore replacement investment (IR) because it is likely to change slowly and not be a significant determinant of the business cycle. We also ignored inventory investment to keep the model simple. More elaborate accelerator models would consider firms adjust their inventories to ensure they can meet unexpected demand changes subject to carrying costs. To add an element of reality to the model we would hypothesises that when making their net investment decisions, firms respond to changes in output last period rather than the current period. Further, in the real world, households adjust their consumption with a lag and so in the following model we use last period’s disposable income as the decision-making variable for households. Combining the acceleration theory of investment with these assumptions, we can write the aggregate expenditure model as: (12.15) Yt = cYt-1 + It = d[vYt-1 – K*t-1] + G + NX where cYt-1 is household consumption and It = d[vYt – K*t-1] is net private investment. For simplicity we assume that the tax rate is zero so we can ignore it and that the propensity to import is zero so NX is just exports. These assumptions allow us to simplify the calculation of the multiplier. We defined K* earlier in the Chapter as being equal to vYt-1. It follows then that K*t-1 = vYt-2. Accordingly, Equation (12.15) can be re-written as: (12.16) Yt = cYt-1 + It = dv[Yt-1 – Yt-2] + G + NX If we had equilibrium, then real GDP is constant which means that Yt = Yt-1 = Yt-2 = Y*. So we can solve Equation (12.16) for its equilibrium or steady-state properties as: (12.16) Y* = cY* + G + NX Note that the Accelerator term drops out when real GDP is constant. We re-arrange Equation (12.16) as follows (calling G + NX = A) (12.16) Y* = 1/(1-c)A Equation (12.16) says that total real income will be a multiple [1/(1-c)] of autonomous spending A. We could have expressed this in terms of the full expenditure multiplier that we derived in Chapter 8, but we lose no explanatory power here by using a simplified expression. As an example, assume the marginal propensity to consume was 0.8 and A was 100. From Equation (12.16) we would solve the equilibrium level of real income to be Y* = 5 x 100 = 500. If, for example, the government increased its autonomous spending and A rose to 120, then the new higher equilibrium national income would be 600. The understanding you gain from these results is that:
So what role does the investment accelerator play? The answer is that once we consider the dynamics of the macroeconomy – the way in which it moves over time – the interaction between the expenditure multiplier and the accelerator becomes relevant. The previous example merely considered two snapshots where the economy was (temporarily) at rest. How it traversed between those two steady-states is the domain of economic dynamics and business cycle analysis. [NOTE – A TABLE IS COMING HERE TO SHOW THE DYNAMICS OF THE SYSTEM] |
Conclusion
That is all I have time for today.
The next section shows the interaction between the multiplier and the accelerator using a numerical and graphical example.
Alternative Olympic Games Medal Tally
My Alternative Olympic Games Medal Tally is now active.
I update it early in the day and again around lunchtime when all the sports are concluded for the day.
That is enough for today!
(c) Copyright 2012 Bill Mitchell. All Rights Reserved.
This is off-topic, but… wouldn’t the message of MMT be more easily understood if it were clearly stated that every financial asset is accompanied by financial liabilty elsewhere in the system? That is why public debt is accompanied by equal amounts of non-government sector wealth. Like mirror image. And when companies go more deeply into debt there must be some couterparty that is gaining assets. When households go into debt to buy property that produces not only debt but equal amounts of financial assets, deposits in the banks. In accounting sense it can be said that all these financial assets net to zero, but in this property buying example households still gain value of their new house, whose value does not net to zero because it is not financial asset.
Logical conclusion is that economy that demands lot of financial assets must have also lots of financial liabilities, i.e. debt. If the demand for financial assets can not be satisfyed aggregate demand falls sort and there is unemployment. Government by issuing its own liabilities can satisfy this demand for financial assets.
And if demand for financial assets is enhanced by government sponsored saving schemes it can be quite huge, overwhelming.
“Kalecki said that budget deficits allow the capitalists to make profits (net exports constant) over and above what their own spending will generate.
Government spending not only directly stimulates aggregate demand but through the multiplier effect it also increases the incomes of household, who, in turn, purchase goods and services from firms.
The opposite is the case.”
The opposite is the case?
Bill, in general I’m suspicious of economic theories based on an equation like your 12.14, where the profit variable is conveniently put on the left side. In my experience, when economists designate one variable to be on the left side of an equation such as this, that is generally followed by some assertion of causality where that left-side variable is claimed to be dependent on the values on the right side, which are generally assumed to be independent of each other. You come very close to at least suggesting, if not claiming, such causal relationships here. I’m sure you understand that the variables in that equation are not independent of each other. The equation as a whole describes mutual constraints among the variables, but says nothing about causality. Causality arguments, it seems to me, should require a completely different sort of theory based on the dynamics of real-world transactions. I’m not a fan of using differential equations for economic modeling because I think they require too many simplifying assumptions about conditions and actions which invalidate them. But I do think there might be other forms of discrete event dynamic modeling that might prove enlightening. In a highly dynamic system with lots of feedback paths, demonstrably accurate models are obviously tough to create. Whether or not the causal relationships you claim here are accurate could, for all we know, be highly dependent on the actual state trajectory of the system at any given point in time.
It seems to me that what you’ve done is to describe in a fairly non-specific way a dynamic theory that seems to be consistent with the constraints described by the equation, but is not really a necessary consequence of them. Note that I’m not actually in any disagreement with your conclusion, because I strongly suspect there is also enough empirical evidence that it is true, at least during some time periods. I’m just wondering about exactly what constitutes a reliable and convincing argument / proof and I’m not sure that I saw that here. I’m also pretty sure that I never would have picked up on that as an undergraduate …
Best of luck on your book, we’re all looking forward to it.
There’s an obvious problem with your writing. In contrast to other macro textbooks, it’s easy to read and makes sense.
“The only time that a rising budget deficit will not add to real profits is if there is full capacity and the rising deficits push nominal aggregate demand beyond the real capacity of the economy to increase output and real income.”
I understand this but the emphasis needs to be on REAL profits since the aggregate nominal profits are not affected by the state of the economy since the sectoral balance law must be satisfied at all times. The real profits are not added to only if there is corresponding inflation. Also, I think we are talking only about monetary profits here. As I understand it, real profits in the form of real goods as opposed to money are a different thing and not subject to the sectoral balance law.
On another point, I find the classificaton of entities as capitalists or householders/workers hard to accept. All capitalists are householders and many, if not most, householders are capitalists because they are shareholders, either directly or through their superannuation. A more natural classification seems to me to be firms and householders. Self employed people would then have a foot in each camp. In any case, I don’t understand properly how share ownership and dividends fit into the formulae for GDP/GNP. I quess I will have to work on that question.
On Laws and Causes
My answer to Paul Krueger would go as follows. Of course, I cannot presume to answer for Bill Mitchell and Randy Wray.
Argument about causes is not relevant in the case of first order MMT description. MMT at this level is an empirical project seeking to discover the empirical facts and Laws of the system and not causes. In terms of the search for knowledge, it is vitally important to distinguish between the search for “Laws” and the search for causes. Taking the example of hard science, the Laws of Physics describe only the apparent invariable relationships between certain quantifiable phenomena. These relationships are discovered by the process of hypothesis-making and hypothesis-testing by experiment; in other words discovered from repeated and verifiable empirical observations and measurements. These apparent invariable relationships we call Laws. We do so once we are sufficiently confident they consistently hold true (within an acceptable range of error) under all observable and conceivable conditions or in a carefully defined range of conditions.
Thus, the famous equation e = mc2, for example, does not assert anything about causality. There is no way we can extract, from Einstein’s famous equation, any notion that matter “causes” energy nor that energy “causes” matter nor even that the interaction of mass and the speed of light “cause” energy. The equation is of mass-energy equivalence (an identity) not of mass-energy conversion. Mass-energy equivalence does not in any way imply that mass is “converted” to energy as mass is always preserved. The three quantities are simply related in an identity statement. (It perhaps allows for matter to be converted to energy but this leads us into very difficult areas, physically and philosophically.) Overall, ontological causality (what causes something to exist) is a non sequitur. Equations like e = mc2 (an identity) from relativity physics or Y = C + I + G + NX (an identity) from MMT do not suggest a temporal relation of before and after nor of progress from cause to effect. They simply assert a point-in-time or a non-temporal (unchanging across time) identity, empirically derived. Mathematically this is expressed in an equation where the equation is satisfied for all values of the involved variables.
So Paul Krueger is strictly correct in saying that the identity equations of MMT “say nothing about causality”. (I am not saying that other parts of MMT say nothing about causality.) In the same way, e=mc2 (an identity equation) also says absolutely nothing about causality. Laws of this kind never say anything about causality, in and of themselves, precisely because they are ontological and mathematical identities. This is not to say these laws are useless or meaningless for later considerations of causality. The real case is far from this. Such Laws, once discovered, are profoundly important to us. They allow the next steps, which are our algorithmically or heuristically guided searches and actions seeking to cause changes in specific quantities over time (for example the quantity of unemployed persons in the economy).
If I might request the indulgence of readers of this blog, I think I can answer the following crucial questions.
How can a seemingly arbitrary and formal human invented system (like the modern financial system) have dependable laws (like physics for example)? Surely, an arbitrary, invented system can take any form and be changed at will thus obviating any chance of its possessing dependable Laws?
Formal invented systems of the class known as models still have dependable internal Laws. Good models even have Laws of relation to the real system being modelled. My particular path to this discovery lay through game system theory and AI theory, particularly the theory of RTS (Real Time Strategy) games. In essence, the issue is to do with systems modelling where the formal system (an actual game or an actual financial economy) attempts to model, quantify and relate by dependable calculations (identities, laws and algorithms) some aspects of the real world.
To ensure we are clear what we are talking about we must note this. The extant financial economy models the real economy. Financial transactions of money units have to model real transactions of goods and services. If there were not some degree of congruency and approach to accuracy, the result would be chaos for the system of individual and national finances and real transfers of goods and services. The financial economy interacts with the real economy too, which is a second order concern and where analysis becomes more complicated. The financial economy even develops its own devices and imperatives and this becomes a third order concern foranalysis.
A macroeconomic model (like MMT) seeks to understand the formal features of the first order financial model of the economy and then seeks to further analyse second order concerns (feedback interactions) and third order concerns which we might call term endogenous financial artifices, expedients and imperatives. So, the extant financial economy is a model of the real economy. MMT, or any macroeconomic theory, is a both a model where it models the real economy and a meta-model (a model of a model) where it models the extant financial economy’s model of the real economy.
All models abstract, simplify and distort real world phenomena. That is the essence of what a model is. It is important to include consideration of the various phenomena of distortion in the analysis. Sometimes, making a model work requires specific intentional distortions (of relativities, values etc) as well as abstraction and simplification. Abstraction and simplification, in and of themselves, imply a degree of unavoidable distortion. By “abstraction” I mean abstracting a discrete quantifiable modelling value from a real world phenomenon which is complex and often at least partly qualitative. Assigning a money value to a real world item or value (a process we undertake ubiquitously and repeatedly in running a money economy) is “abstracting”.
What I have found from game system modelling and AI theory is that all internally consistent model systems have Laws as well as rules. Rules are “the rules of the game”. For example chess has rules; rules that govern the size of the board (a two dimensional delimited of array 8×8), the moves of the pieces and the rights and obligations of players and bystanders. Though these are formally called the Laws of Chess it is better for our purposes to call them the Rules of Chess. The word “Laws” must be reserved for a another, clearly defined use. Chess is part of a genre of games which we might call turn based array games. Chess, draughts, noughts-and-crosses, tic-tac-toe (3 dimensional noughts-and-crosses) and 3 dimensional chess are all examples of this genre. What we find is that games of this genre exhibit consistent and dependable laws which are unaffected by rule changes or parameter changes provided the fundamental nature of the genre (games of dimensioned, delimited arrays, with alternate turns and movement by discrete quanta) remains intact. An example of such a Law is that any piece with any kind of omni-directional move or influence “controls” more array elements (squares in chess) from the centre of the array than it does from a side or corner of the array. This would not be true for a “wrap-around array” game which thus by definition would belong to a different genre.
What MMT theorists have done in essence (from my point of view) is take a model with relatively consistent and delineable rules, the Modern Monetary System, and first enumerate the rules and parameters of the genre (MMS mixed economy capitalism) and then second, derive the consistent Laws of this genre of models.
In game theory, it is clear that each genre of game models partakes of the same essential law-bound nature as the real physical world, though genre does so in its own particular way. There are clear reasons for this. The physical (and even biological) Laws of the real world impose both “hard” and “elastic” constraints on the game world; on the model world in other words. The Laws of the real world (some of them) ineluctably push into and impose themselves on the models. A very central example is dimensionality. We are familiar with the notion that we live in a world of four obvious dimensions. These are height, width and depth (the x, y and z axes of 3D space) plus time. A game with a geometric basis, like chess as mentioned above, need not model all the space dimensions but it must model some (two in the case of chess). A chess board models two space dimensions and is a finite two-dimensional array (8 x 8). Thus, the internal Laws of chess consistently reflect some aspects of the physical dimension-conditioned Laws of the real world.
An example of an in-game “Law” in chess, given above, is that a piece will “control” more squares from the centre of the board than it does from the corner of the board. This is mathematically and geometrically axiomatic. This “control” is a movement potential dependent on the movement rules of chess and on obstacles imposed by other pieces on the board and the board’s array limits. This Law has its direct physical analogue in the real world where, for example, I can sweep more horizontal area with my arms while standing in the centre of the room than I can while standing in a corner of the room. The crucial thing about all such in-model Laws, where the model models the real world in some way, is that they are mathematically/geometrically axiomatic in-model and their direct analogues are also empirically true in the real world.
Thus, asserting (for example) that all models of a game genre like RTS have the same reliable basic internal Laws is really asserting no more than the following. RTS games are all of a structure which models the three space dimensions plus time as the arena of action and then models and places simulacra of materials, energies and units (machine or human representations) within that 3D, time-dependent world. All these features can be, and indeed must be, quantified. They are governed by mathematical-geometric Laws analogous to the classical Laws of physics of the real world. These laws are explicitly analogous in those modern games which use Newtonian physics engines.
To sum up we can state;
• Laws describe the invariable relationships in a system. Hence Laws (correctly derived) are unchallengeable.
• RTS computer games are mathematically, geometrically and algorithmically governed systems models of the real world and as such they have invariable relationships both internally and with regard to the real world which they model. These relationships can be described by Laws.
We then find, for example, that simplistic Euclidean laws like “the shortest distance between two points is a straight line” are true in the real world and in the game world provided the (local) geometry is of a precisely or closely approximate Euclidean nature in both cases. At a slightly more complex level, we then find that the military law of strategic attenuation (it gets harder to project military power over greater distances) applies equally in the real world and in the modelled world of the game (provided the model is accurate in its essentials).
Where this theory gets really interesting and could cross over into good macroeconomic modelling, in my opinion, is when we discover that each genre model, be it a game model of the real world or an economic model of the real world, begins to demonstrate what I call System Meta-Laws (SMLs). The idea of using this word for this new concept is suggested by the term “metadata”. Simplistically, “metadata” means data about data but it can also mean the discipline of creating structures for data. The structural metadata field is concerned with the design and specification of data structures.
Similarly, System Meta-Law (SML) is concerned with the design, specification, building and use of complex mathematic-geometric-algorithmic (MGA) systems. RTS (Real Time Strategy) is such a system. The Modern Monetary System (MMS) is such a system. Each discrete, though complex, MGA system will have its own unique set of System Meta-Laws and these must be derived from the Laws of the particular MGA system under consideration. System Meta-Laws will allow us to;
• Guide goal-seeking design of a complex MGA system from concept design onwards.
• Guide goal-seeking construction (or amendment) of a complex MGA system.
• Guide the fit of the complex MGA system to desires, needs and abilities of human users.
• Guide goal-seeking execution of tasks in the completed complex MGA system itself.
To reiterate, System Meta-Laws (SMLs) must be derived from the intrinsic laws of the mathematical-geometrical-algorithmic (MGA) system in question. Thus deriving SMLs is a two stage process. First the intrinsic Laws of the MGA system must be discovered and proven logically and mathematically. Second, the SMLs must be derived and expressed in a form which I describe as a “Firm Heuristic” (as opposed to a rough or loose heuristic). A firm heuristic is a firm and dependable goal-seeking guide. What we are saying when we derive a firm heuristic from MGA System Laws is this. The MGA Laws of this system (provable in mathematical terms) comprehensively suggest this Meta-Law heuristic to us and further suggest that it is substantially correct, to the point where we can deduce that it too (the SML) would be provable mathematically if it were not for the exponential problems of combinatorial mathematics and/or the sometimes necessary inclusion of qualitative terms and goals. In summary, each MGA system genre (including RTS or the MMS) has intrinsic Laws and thus design, re-design and execution (game-play or economic activity) must have System Meta-laws or what could also be called Structure-Conditioned Meta-Laws.
Now obviously I have not done MMT work nor have I done the work of formally proving that the MMS (the Modern Monetary System or actual money and financial system) as a first order model of the real economy is a model with internal invariable laws and certain invariable relations (also laws) with the real economy. Nor have I enumerated the MMS’s comprehensive and relatively consistent internal rule set nor the empirical reasons for MMS having not these only internal laws but also (some) laws of invariable relation with the real world. Yet I am confident that these laws exist and are discoverable. One clear law of relation between the extant financial system (which I call the MMS model) and the real world economy of real materials, energies, agents, goods, processes and services is that both exhibit time dependency. This point is fundamental, not trivial. There will be inflexible laws of time dependency linking the two. Accounting would not be possible if this were not so.
Finally, I am no expert on MMT, but Bill Mitchell’s derivation of this fact – that a capitalist economy of the MMS mixed economy variety will exhibit ineluctably either a requirement for unemployment buffer stocks or employment buffer stocks of the form defined and implemented by a job guarantee – is indeed a System Meta-Law. That is to say, the MGA (mathematic-geometric-algorithmic) Laws of the system (provable in mathematical terms) comprehensively suggest this Meta-Law firm heuristic to us and further suggest that it is very substantially correct, to the point where we can deduce that it too (the System Meta-Law) would be provable mathematically were it not for the exponential problems of combinatorial mathematics and/or the sometimes necessary inclusion of qualitative terms and goals.