The Weekend Quiz – September 28-29, 2019 – answers and discussion

September 28, 2019
bill
Saturday quiz
0 Comments

Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

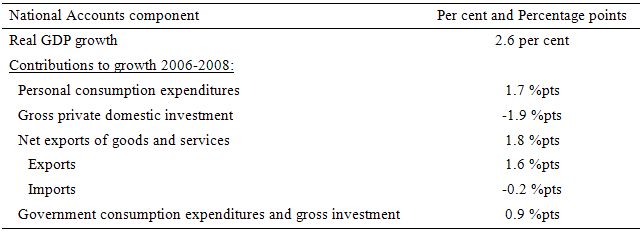
From the US National Accounts, you find that in 2006, the share of Personal consumption expenditure in real GDP was 69.9 per cent and by 2008 it had fallen to 69.8 per cent. Similarly, the share of Gross private domestic investment on real GDP was 17.2 per cent in 2006 and by 2008 had fallen to 14.9 per cent (and further to 11.8 per cent in 2009). The net export deficit over the same period (2006 to 2008) fell from -5.7 per cent of real GDP to -4.9 per cent in 2008. Finally, the share of Government consumption expenditures and gross investment in real GDP rose from 18.8 per cent in 2006 to 18.9 per cent in 2008 (and 19.7 per cent in 2009). These relative changes tell you that real GDP was lower in 2008 compared to 2006 because the increase in Government spending and the falling negative contribution of net exports were not sufficient to offset the declining contribution from consumption and investment.

The answer is False.

The detail in the question relates to expenditure shares in real GDP and clearly does not tell you anything about the growth in GDP. All that you are being told are that the shares are changing over the period 2006 to 2008 in favour of public spending.

The shares are given by the following equation:

where A(t) is the value of aggregate A in quarter under consideration (say Personal consumption expenditure) and GDP(t) is the value of GDP in the same quarter.

So a change in the public spending share from 18.8 per cent in 2006 to 18.9 per cent in 2008 just says that in 2008 the flow of public spending is a greater proportion of the flow of real output in 2008 than it was in 2006. The rising share could be associated with a declining, constant or growing real GDP.

The fact you know that over this time that real GDP growth in the US was falling is irrelevant – the question asks whether you can conclude from the information before you.

The other related measure is the contributions to GDP growth which tell you each quarter what the expenditure components contributed to the GDP growth in that quarter.

From the Australian National Accounts – December 2009 you can find the definition of the contributions to GDP growth which is represented by the following equation:

where A(t) is as before; A(t-1) – value of aggregate A in previous quarter; and GDP(t-1) – value of GDP in previous quarter.

The ABS indicate that “the contributions to growth of the components of GDP do not always add exactly to the growth in GDP. This can happen as a result of rounding and the lack of additivity of the chain volume estimates prior to the latest complete financial year.

From the US National Accounts data you see that real GDP grew in 2005-06 by 2.7 per cent; then slowed to 2.1 per cent in 2006-07, 0.4 per cent in 2007-08 and plunged to -2.4 per cent in 2008-09. Over the period 2006-2008, real GDP grew overall by 2.6 per cent. The following table breaks down the contributions to that growth by the individual spending components (computed as per the Equation above).

The point of the question (if any) is to warn you into being careful to clarify the concepts being used before drawing conclusions. Too many people think they know what these terms mean and either mis-use them themselves to reach erroneous conclusions or allow themselves to be fooled by others who are touting erroneous conclusions.

If you are interested in more detail on national accounts then the 5216.0 – Australian National Accounts: Concepts, Sources and Methods, 2000 – is the place to go. Recommended reading if you want to get all the concepts and stock-flow relationships really sorted out. The system is universal and used by all statistical agencies.

Question 2:

Assume that a standard monthly Labour Force data release showed that employment grew by only 400 in net terms during the last month. Other highlights were that unemployment rose by 10,700 and that the labour force participation rate fell by 0.1 per cent indicating a rise in the proportion leaving the labour force. Taken together this data tells you that:

(a) The labour force grew faster than employment but not as fast the working age population.

(b) The working age population grew faster than employment and offset the decline in the labour force arising from the drop in the participation rate.

(c) The labour force grew faster than employment but you cannot tell what happened to the working age population from the information provided. ‘

The answer is Option (a) The labour force grew faster than employment but not as fast the working age population.

If you didn’t get this correct then it is likely you lack an understanding of the labour force framework which is used by all national statistical offices.

The labour force framework is the foundation for cross-country comparisons of labour market data. The framework is made operational through the International Labour Organization (ILO) and its International Conference of Labour Statisticians (ICLS). These conferences and expert meetings develop the guidelines or norms for implementing the labour force framework and generating the national labour force data.

The rules contained within the labour force framework generally have the following features:

an activity principle, which is used to classify the population into one of the three basic categories in the labour force framework;
a set of priority rules, which ensure that each person is classified into only one of the three basic categories in the labour force framework; and
a short reference period to reflect the labour supply situation at a specified moment in time.

The system of priority rules are applied such that labour force activities take precedence over non-labour force activities and working or having a job (employment) takes precedence over looking for work (unemployment). Also, as with most statistical measurements of activity, employment in the informal sectors, or black-market economy, is outside the scope of activity measures.

Paid activities take precedence over unpaid activities such that for example ‘persons who were keeping house’ as used in Australia, on an unpaid basis are classified as not in the labour force while those who receive pay for this activity are in the labour force as employed.

Similarly persons who undertake unpaid voluntary work are not in the labour force, even though their activities may be similar to those undertaken by the employed. The category of ‘permanently unable to work’ as used in Australia also means a classification as not in the labour force even though there is evidence to suggest that increasing ‘disability’ rates in some countries merely reflect an attempt to disguise the unemployment problem.

The following diagram shows the complete breakdown of the categories used by the statisticians in this context. The yellow boxes are relevant for this question.

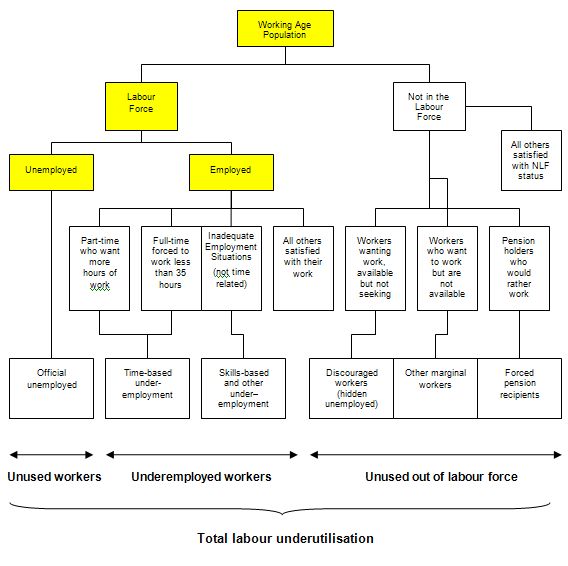
So the Working Age Population (WAP) is usually defined as those persons aged between 15 and 65 years of age or increasing those persons above 15 years of age (recognising that official retirement ages are now being abandoned in many countries).

As you can see from the diagram the WAP is then split into two categories: (a) the Labour Force (LF) and; (b) Not in the Labour Force – and this divisision is based on activity tests (being in paid employed or actively seeking and being willing to work).

The Labour Force Participation Rate is the percentage of the WAP that are active. So in the case above, if the current Australian participation rate overall is 65.2 per cent. This means that 65.2 per cent of those persons above the age of 15 are actively engaged in the labour market (either employed or unemployed).

You can also see that the Labour Force is divided into employment and unemployment. Most nations use the standard demarcation rule that if you have worked for one or more hours a week during the survey week you are classified as being employed.

If you are not working but indicate you are actively seeking work and are willing to currently work then you are considered to be unemployed. If you are not working and indicate either you are not actively seeking work or are not willing to work currently then you are considered to be Not in the Labour Force.

So you get the category of hidden unemployed who are willing to work but have given up looking because there are no jobs available. The statistician counts them as being outside the labour force even though they would accept a job immediately if offered.

The question gave you information about employment, unemployment and the labour force participation rate and you had to deduce the rest based on your understanding.

In terms of the Diagram the following formulas link the yellow boxes:

Labour Force = Employment + Unemployment = Labour Force Participation Rate times the Working Age Population

It follows that the Working Age Population is derived as Labour Force divided by the Labour Force Participation Rate (appropriately scaled in percentage point units).

So if both Employment and Unemployment is growing then you can conclude that the Labour Force is growing by the sum of the extra Employment and Unemployment expressed as a percentage of the previous Labour Force.

The Labour Force can grow in one of four ways:

Working Age Population growing with the labour force participation rate constant;
Working Age Population growing and offsetting a falling labour force participation rate;
Working Age Population constant and the labour force participation rate rising;
Working Age Population falling but being offset by a rising labour force participation rate.

So in our case, if the Participation Rate is falling then the proportion of the Working Age Population that is entering the Labour Force is falling. So for the Labour Force to be growing the Working Age Population has to be growing faster than the Labour Force.

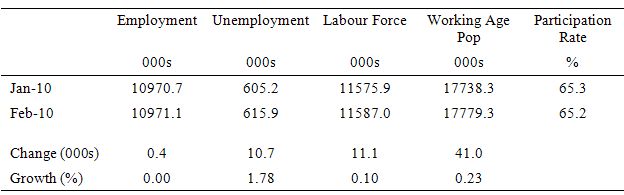
Now consider the following Table which shows the Australian labour force aggregates for January and February 2010 (the same that were used in the question).

You can see added information which demonstrates the point.

So the correct answer is as above.

Of the second option:

The working age population grew faster than employment and offset the decline in the labour force arising from the drop in the participation rate.

Clearly impossible if both employment and unemployment both rose.

And of the third option:

The labour force grew faster than employment but you cannot tell what happened to the working age population from the information provided.

Clearly you can tell what happened to the working age population by deduction.

Question 3:

If the household saving ratio rises and there is an external deficit then Modern Monetary Theory tells us that the government must increase net spending or else national output and income will fall.

The answer is False.

This question tests one’s basic understanding of the sectoral balances that can be derived from the National Accounts. The secret to getting the correct answer is to realise that the household saving ratio is not the overall sectoral balance for the private domestic sector.

In other words, if you just compared the household saving ratio with the external deficit and the fiscal balance you would be leaving an essential component of the private domestic balance out – private capital formation (investment).

To understand that, in macroeconomics we have a way of looking at the national accounts (the expenditure and income data) which allows us to highlight the various sectors – the government sector and the non-government sector (and the important sub-sectors within the non-government sector).

To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

(1) GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.

We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all tax revenue minus total transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).

Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).

Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):

(2) GNP = C + I + G + (X – M) + FNI

To render this approach into the sectoral balances form, we subtract total net taxes (T) from both sides of Expression (3) to get:

(3) GNP – T = C + I + G + (X – M) + FNI – T

Now we can collect the terms by arranging them according to the three sectoral balances:

(4) (GNP – C – T) – I = (G – T) + (X – M + FNI)

The the terms in Expression (4) are relatively easy to understand now.

The term (GNP – C – T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.

The left-hand side of Equation (4), (GNP – C – T) – I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP – C – T).

In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.

The term (G – T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.

Finally, the other right-hand side term (X – M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.

In English we could say that:

The private financial balance equals the sum of the government financial balance plus the current account balance.

We can re-write Expression (6) in this way to get the sectoral balances equation:

(5) (S – I) = (G – T) + CAB

which is interpreted as meaning that government sector deficits (G – T > 0) and current account surpluses (CAB > 0) generate national income and net financial assets for the private domestic sector.

Conversely, government surpluses (G – T < 0) and current account deficits (CAB < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets.

Expression (5) can also be written as:

(6) [(S – I) – CAB] = (G – T)

where the term on the left-hand side [(S – I) – CAB] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance.

This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit).

The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers.

All these relationships (equations) hold as a matter of accounting and not matters of opinion.

You can then manipulate these balances to tell stories about what is going on in a country.

For example, when an external deficit (X – M < 0) and a public surplus (G – T < 0) coincide, there must be a private domestic deficit.

So if X = 10 and M = 20, X – M = -10 (a current account deficit) and if G = 20 and T = 30, G – T = -10 (a fiscal surplus), then the right-hand side of the sectoral balances equation (5) above, will equal (20 – 30) + (10 – 20) = -20.

As a matter of accounting then (S – I) = -20 which means that the domestic private sector is spending more than they are earning because I > S by 20 (whatever $ units we like).

So the fiscal drag from the public sector is coinciding with an influx of net savings from the external sector.

While private spending can persist for a time under these conditions using the net savings of the external sector, the private sector becomes increasingly indebted in the process. It is an unsustainable growth path.

So if a nation usually has a current account deficit (X – M < 0) then if the private domestic sector is to net save (S – I) > 0, then the public deficit has to be large enough to offset the current account deficit.

Say, (X – M) = -20 (as above). Then a balanced fiscal position (G – T = 0) will force the domestic private sector to spend more than they are earning (S – I) = -20.

But a government deficit of 25 (for example, G = 55 and T = 30) will give a right-hand solution of (55 – 30) + (10 – 20) = 15. The domestic private sector can net save.

So by only focusing on the household saving ratio in the question, I was only referring to one component of the private domestic balance. Clearly in the case of the question, if private investment is strong enough to offset the household desire to increase saving (and withdraw from consumption) then no spending gap arises.

In the present situation in most countries, households have reduced the growth in consumption (as they have tried to repair overindebted balance sheets) at the same time that private investment has fallen dramatically.

As a consequence a major spending gap emerged that could only be filled in the short- to medium-term by government deficits if output growth was to remain intact.

The reality is that the fiscal deficits were not large enough and so income adjustments (negative) occurred and this brought the sectoral balances in line at lower levels of economic activity.

The following blog posts may be of further interest to you:

That is enough for today!