The Weekend Quiz – June 9-10, 2018 – answers and discussion

Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

Real wages growth has been non-existent or low in many advanced nations in recent years. However, if workers succeed in gaining real wages increases then this will squeeze the share of profits in national income.

The answer is False.

The question requires you to understand what determines the real wage and what the relationship between earnings and labour productivity growth is. When economists do not specify the unit you should always assume they are talking in nominal terms. So the reference to the “rate of growth of earnings” is in terms of the monetary unit which is the common understanding that people would have of the term.

In terms of the logic of the question, that would also be the only sensible interpretation.

The real wage is defined as the purchasing power equivalent on the nominal wage that workers get paid each period. To compute the real wage we need to consider two variables: (a) the nominal wage (W) and the aggregate price level (P).

We might consider the aggregate price level to be measured by the consumer price index (CPI) although there are huge debates about that. But in a sense, this macroeconomic price level doesn’t exist but represents some abstract measure of the general movement in all prices in the economy.

Macroeconomics is hard to learn because it involves these abstract variables that are never observed – like the price level, like “the interest rate” etc. They are just stylisations of the general tendency of all the different prices and interest rates.

Now the nominal wage (W) – that is paid by employers to workers is determined in the labour market – by the contract of employment between the worker and the employer. The price level (P) is determined in the goods market – by the interaction of total supply of output and aggregate demand for that output although there are complex models of firm price setting that use cost-plus mark-up formulas with demand just determining volume sold. We shouldn’t get into those debates here.

The inflation rate is just the continuous growth in the price level (P). A once-off adjustment in the price level is not considered by economists to constitute inflation.

So the real wage (w) tells us what volume of real goods and services the nominal wage (W) will be able to command and is obviously influenced by the level of W and the price level. For a given W, the lower is P the greater the purchasing power of the nominal wage and so the higher is the real wage (w).

We write the real wage (w) as W/P. So if W = 10 and P = 1, then the real wage (w) = 10 meaning that the current wage will buy 10 units of real output. If P rose to 2 then w = 5, meaning the real wage was now cut by one-half.

The relationship between the real wage and labour productivity relates to movements in the unit costs, real unit labour costs and the wage and profit shares in national income.

The wage share in nominal GDP is expressed as the total wage bill as a percentage of nominal GDP. Economists differentiate between nominal GDP ($GDP), which is total output produced at market prices and real GDP (GDP), which is the actual physical equivalent of the nominal GDP. We will come back to that distinction soon.

To compute the wage share we need to consider total labour costs in production and the flow of production ($GDP) each period.

Employment (L) is a stock and is measured in persons (averaged over some period like a month or a quarter or a year.

The wage bill is a flow and is the product of total employment (L) and the average wage (w) prevailing at any point in time. Stocks (L) become flows if it is multiplied by a flow variable (W). So the wage bill is the total labour costs in production per period.

So the wage bill = W.L

The wage share is just the total labour costs expressed as a proportion of $GDP – (W.L)/$GDP in nominal terms, usually expressed as a percentage. We can actually break this down further.

Labour productivity (LP) is the units of real GDP per person employed per period. Using the symbols already defined this can be written as:

LP = GDP/L

so it tells us what real output (GDP) each labour unit that is added to production produces on average.

Nominal GDP ($GDP) can be written as P.GDP, where the P values the real physical output.

Now if you put of these concepts together you get an interesting framework. To help you follow the logic here are the terms developed and be careful not to confuse $GDP (nominal) with GDP (real):

• Wage share = (W.L)/$GDP
• Nominal GDP: $GDP = P.GDP
• Labour productivity: LP = GDP/L
• Real wage: w = W/P

By substituting the expression for Nominal GDP into the wage share measure we get:

Wage share = (W.L)/P.GDP

In this area of economics, we often look for alternative way to write this expression – it maintains the equivalence (that is, obeys all the rules of algebra) but presents the expression (in this case the wage share) in a different “view”.

So we can write as an equivalent:

Wage share – (W/P).(L/GDP)

Now if you note that (L/GDP) is the inverse (reciprocal) of the labour productivity term (GDP/L). We can use another rule of algebra (reversing the invert and multiply rule) to rewrite this expression again in a more interpretable fashion.

So an equivalent but more convenient measure of the wage share is:

Wage share = (W/P)/(GDP/L) – that is, the real wage (W/P) divided by labour productivity (GDP/L).

I won’t show this but I could also express this in growth terms such that if the growth in the real wage equals labour productivity growth the wage share is constant. The algebra is simple but we have done enough of that already.

That journey might have seemed difficult to non-economists (or those not well-versed in algebra) but it produces a very easy to understand formula for the wage share.

Two other points to note. The wage share is also equivalent to the real unit labour cost (RULC) measures that Treasuries and central banks use to describe trends in costs within the economy. Please read my blog – Saturday Quiz – May 15, 2010 – answers and discussion – for more discussion on this point.

Now it becomes obvious that if the nominal wage (W) and the price level (P) are growing at the pace the real wage is constant. And if the real wage is growing at the same rate as labour productivity, then both terms in the wage share ratio are equal and so the wage share is constant.

The wage share was constant for a long time during the Post Second World period and this constancy was so marked that Kaldor (the Cambridge economist) termed it one of the great “stylised” facts. So real wages grew in line with productivity growth which was the source of increasing living standards for workers.

The productivity growth provided the “room” in the distribution system for workers to enjoy a greater command over real production and thus higher living standards without threatening inflation.

Since the mid-1980s, the neo-liberal assault on workers’ rights (trade union attacks; deregulation; privatisation; persistently high unemployment) has seen this nexus between real wages and labour productivity growth broken. So while real wages have been stagnant or growing modestly, this growth has been dwarfed by labour productivity growth.

The following blogs may be of further interest to you:

• The origins of the economic crisis
• The fiscal stimulus worked but was captured by profits

Question 2:

The government has to issue debt to match an on-going fiscal deficit if the central bank is targetting, say a 2 per cent short-term interest rate and declines to pay a return on excess bank reserves.

The answer is True.

I am using the term government here in the Modern Monetary Theory (MMT) sense of the consolidation of the central bank and treasury operations.

Central banks conducts what are called liquidity management operations for two reasons. First, they have to ensure that all private cheques (that are funded) clear and other interbank transactions occur smoothly as part of its role of maintaining financial stability. Second, they must maintain aggregate bank reserves at a level that is consistent with their target policy setting given the relationship between the two.

So operating factors link the level of reserves to the monetary policy setting under certain circumstances. These circumstances require that the return on “excess” reserves held by the banks is below the monetary policy target rate. In addition to setting a lending rate (discount rate), the central bank also sets a support rate which is paid on commercial bank reserves held by the central bank.

Commercial banks maintain accounts with the central bank which permit reserves to be managed and also the clearing system to operate smoothly. In addition to setting a lending rate (discount rate), the central bank also can set a support rate which is paid on commercial bank reserves held by the central bank (which might be zero).

Many countries (such as Australia, Canada and zones such as the European Monetary Union) maintain a default return on surplus reserve accounts (for example, the Reserve Bank of Australia pays a default return equal to 25 basis points less than the overnight rate on surplus Exchange Settlement accounts). Other countries like Japan and the US have typically not offered a return on reserves until the onset of the current crisis.

If the support rate is zero then persistent excess liquidity in the cash system (excess reserves) will instigate dynamic forces which would drive the short-term interest rate to zero unless the government sells bonds (or raises taxes). This support rate becomes the interest-rate floor for the economy.

The short-run or operational target interest rate, which represents the current monetary policy stance, is set by the central bank between the discount and support rate. This effectively creates a corridor or a spread within which the short-term interest rates can fluctuate with liquidity variability. It is this spread that the central bank manages in its daily operations.

In most nations, commercial banks by law have to maintain positive reserve balances at the central bank, accumulated over some specified period. At the end of each day commercial banks have to appraise the status of their reserve accounts. Those that are in deficit can borrow the required funds from the central bank at the discount rate.

Alternatively banks with excess reserves are faced with earning the support rate which is below the current market rate of interest on overnight funds if they do nothing. Clearly it is profitable for banks with excess funds to lend to banks with deficits at market rates. Competition between banks with excess reserves for custom puts downward pressure on the short-term interest rate (overnight funds rate) and depending on the state of overall liquidity may drive the interbank rate down below the operational target interest rate. When the system is in surplus overall this competition would drive the rate down to the support rate.

The main instrument of this liquidity management is through open market operations, that is, buying and selling government debt. When the competitive pressures in the overnight funds market drives the interbank rate below the desired target rate, the central bank drains liquidity by selling government debt. This open market intervention therefore will result in a higher value for the overnight rate. Importantly, we characterise the debt-issuance as a monetary policy operation designed to provide interest-rate maintenance. This is in stark contrast to orthodox theory which asserts that debt-issuance is an aspect of fiscal policy and is required to finance deficit spending.

So the fundamental principles that arise in a fiat monetary system are as follows.

• The central bank sets the short-term interest rate based on its policy aspirations.
• Government spending is independent of borrowing which the latter best thought of as coming after spending.
• Government spending provides the net financial assets (bank reserves) which ultimately represent the funds used by the non-government agents to purchase the debt.
• Budget deficits put downward pressure on interest rates contrary to the myths that appear in macroeconomic textbooks about ‘crowding out’.
• The “penalty for not borrowing” is that the interest rate will fall to the bottom of the “corridor” prevailing in the country which may be zero if the central bank does not offer a return on reserves.
• Government debt-issuance is a “monetary policy” operation rather than being intrinsic to fiscal policy, although in a modern monetary paradigm the distinctions between monetary and fiscal policy as traditionally defined are moot.

Accordingly, debt is issued as an interest-maintenance strategy by the central bank. It has no correspondence with any need to fund government spending. Debt might also be issued if the government wants the private sector to have less purchasing power.

Further, the idea that governments would simply get the central bank to “monetise” treasury debt (which is seen orthodox economists as the alternative “financing” method for government spending) is highly misleading. Debt monetisation is usually referred to as a process whereby the central bank buys government bonds directly from the treasury.

In other words, the federal government borrows money from the central bank rather than the public. Debt monetisation is the process usually implied when a government is said to be printing money. Debt monetisation, all else equal, is said to increase the money supply and can lead to severe inflation.

However, as long as the central bank has a mandate to maintain a target short-term interest rate, the size of its purchases and sales of government debt are not discretionary. Once the central bank sets a short-term interest rate target, its portfolio of government securities changes only because of the transactions that are required to support the target interest rate.

The central bank’s lack of control over the quantity of reserves underscores the impossibility of debt monetisation. The central bank is unable to monetise the federal debt by purchasing government securities at will because to do so would cause the short-term target rate to fall to zero or to the support rate. If the central bank purchased securities directly from the treasury and the treasury then spent the money, its expenditures would be excess reserves in the banking system. The central bank would be forced to sell an equal amount of securities to support the target interest rate.

The central bank would act only as an intermediary. The central bank would be buying securities from the treasury and selling them to the public. No monetisation would occur.

However, the central bank may agree to pay the short-term interest rate to banks who hold excess overnight reserves. This would eliminate the need by the commercial banks to access the interbank market to get rid of any excess reserves and would allow the central bank to maintain its target interest rate without issuing debt.

The following blogs may be of further interest to you:

• Saturday Quiz – May 1, 2010 – answers and discussion
• Understanding central bank operations
• Building bank reserves will not expand credit
• Building bank reserves is not inflationary
• Deficit spending 101 – Part 1
• Deficit spending 101 – Part 2
• Deficit spending 101 – Part 3

Question 3:

Suppose that the government announced it intended to cut its deficit from 4 per cent of GDP to 2 per cent in the coming year and during that year net exports were projected to move from a deficit of 1 per cent of GDP to a surplus of 1 per cent of GDP. If private sector deleveraging resulted in it spending less than it earned to the measure of 5 per cent of GDP, then the fiscal austerity plans will undermine growth even if the net export surplus was realised.

The answer is True.

This question requires an understanding of the sectoral balances that can be derived from the National Accounts. But it also requires some understanding of the behavioural relationships within and between these sectors which generate the outcomes that are captured in the National Accounts and summarised by the sectoral balances.

From an accounting sense, if the external sector goes into surplus (positive net exports) there is scope for the government balance to move into surplus without compromising growth as long as the external position (injection of spending) more than offsets any actual private domestic sector net saving.

In that sense, the strategy requires net exports adding more to aggregate demand than is destroyed by the government via its fiscal austerity. But it also implicitly assumes the private domestic sector will not undermine the strategy via increased saving overall.

To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

(1) GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.

We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all tax revenue minus total transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).

Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).

Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):

(2) GNP = C + I + G + (X – M) + FNI

To render this approach into the sectoral balances form, we subtract total net taxes (T) from both sides of Expression (3) to get:

(3) GNP – T = C + I + G + (X – M) + FNI – T

Now we can collect the terms by arranging them according to the three sectoral balances:

(4) (GNP – C – T) – I = (G – T) + (X – M + FNI)

The the terms in Expression (4) are relatively easy to understand now.

The term (GNP – C – T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.

The left-hand side of Equation (4), (GNP – C – T) – I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP – C – T).

In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.

The term (G – T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.

Finally, the other right-hand side term (X – M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.

In English we could say that:

The private financial balance equals the sum of the government financial balance plus the current account balance.

We can re-write Expression (6) in this way to get the sectoral balances equation:

(5) (S – I) = (G – T) + CAD

which is interpreted as meaning that government sector deficits (G – T > 0) and current account surpluses (CAD > 0) generate national income and net financial assets for the private domestic sector.

Conversely, government surpluses (G – T < 0) and current account deficits (CAD < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets.

Expression (5) can also be written as:

(6) [(S – I) – CAD] = (G – T)

where the term on the left-hand side [(S – I) – CAD] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance.

This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit).

The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers.

All these relationships (equations) hold as a matter of accounting and not matters of opinion.

If the nation is running an external surplus it means that the contribution to aggregate demand from the external sector is positive – that is net spending injection – providing a boost to domestic production and income generation.

The extent to which this allows the government to reduce its deficit (by the same amount as the run a surplus equal to the external balance and not endanger growth depends on the private domestic sector’s spending decisions (overall). If the private domestic sector runs a deficit, then the EU/IMF/ECB strategy will work under the assumed conditions – inasmuch as the goal is to reduce the fiscal deficit without compromising growth.

But this strategy would be unsustainable as it would require the private domestic sector overall to continually increase its indebtedness.

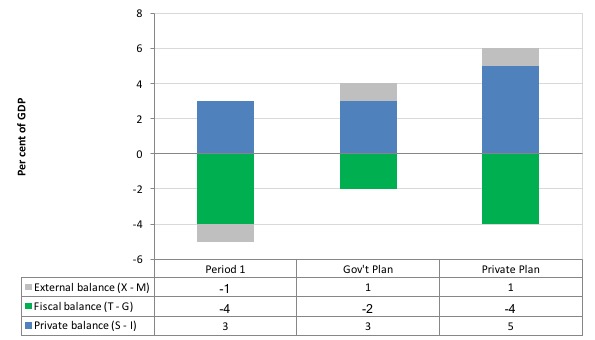
The following graph captures what might happen if the private domestic sector (households and firms) seeks to increase its overall saving at the same time the net exports are rising and the government deficit is falling.

In Period 1, there is an external deficit of 1 per cent of GDP and a fiscal deficit of 4 per cent of GDP which generates income sufficient to allow the private domestic sector to save 3 per cent of GDP.

The Government plans to cut its deficit to 2 per cent of GDP by cutting spending. To achieve that at the same time that net exports is rising to 1 per cent of GDP then the government would be implicitly assuming that the private domestic sector would not change its saving behaviour overall.

However, what happens if the private sector, fearing the contractionary forces coming from the announced cuts in public spending and not really being in a position to assess what might happen to net exports over the coming period, decides to increase its saving. In other words, they plan to increase net saving to 5 per cent of GDP – the situation captured under the Private Plan option.

In this case, if the private domestic sector actually succeeded in reducing its spending and increasing its saving balance to 5 per cent of GDP, the income shifts would ensure the government could not realise its planned deficit reduction.

The public and private plans are clearly not compatible and the resolution of their competing objectives would be achieved by income shifts.

In other words, as the private domestic sector and the public sector reduced their spending in pursuit of their plans, income would contract even though net exports were rising.

The situation is that unless private domestic sector behaviour remains constant the government cannot rely on an increase in net exports to provide the space for them to cut their own net spending.

So in general, with the government net spending contracting, the only way the private domestic sector could successfully increase its net saving is if the injection from the external sector offset the drain from the domestic sector (public and private).

Otherwise, income will decline and both the government and private domestic sector will find it difficult to reduce their net spending positions.

Take a balanced fiscal position, then income will decline unless the private domestic sector’s saving overall is just equal to the external surplus. If the private domestic sector tried to push its position further into surplus then the following story might unfold.

Consistent with this aspiration, households may cut back on consumption spending and save more out of disposable income. The immediate impact is that aggregate demand will fall and inventories will start to increase beyond the desired level of the firms.

The firms will soon react to the increased inventory holding costs and will start to cut back production. How quickly this happens depends on a number of factors including the pace and magnitude of the initial demand contraction. But if the households persist in trying to save more and consumption continues to lag, then soon enough the economy starts to contract – output, employment and income all fall.

The initial contraction in consumption multiplies through the expenditure system as workers who are laid off also lose income and their spending declines. This leads to further contractions.

The declining income leads to a number of consequences. Net exports improve as imports fall (less income) but the question clearly assumes that the external sector remains in deficit. Total saving actually starts to decline as income falls as does induced consumption.

So the initial discretionary decline in consumption is supplemented by the induced consumption falls driven by the multiplier process.

The decline in income then stifles firms’ investment plans – they become pessimistic of the chances of realising the output derived from augmented capacity and so aggregate demand plunges further. Both these effects push the private domestic balance further towards and eventually into surplus

With the economy in decline, tax revenue falls and welfare payments rise which push the public fiscal balance towards and eventually into deficit via the automatic stabilisers.

If the private domestic sector persists in trying to increase its saving ratio then the contracting income will clearly push the fiscal balance into deficit.

So the external position has to be sufficiently strong enough to offset the domestic drains on expenditure.

The following blogs may be of further interest to you:

• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!

That is enough for today!

(c) Copyright 2018 William Mitchell. All Rights Reserved.