The Weekend Quiz – February 3-4, 2018 – answers and discussion

Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

When an economy is running a current account deficit, only one of the two remaining sectors (government or private domestic) can be in surplus, irrespective of the GDP growth rate.

The answer is True.

Once again it is a test of one’s basic understanding of the sectoral balances that can be derived from the National Accounts.

When the external sector is in deficit, then it is impossible for both the private domestic sector and government sector to run surpluses. At least one of those two has to also be in deficit to satisfy the accounting rules.

National income movements will always deliver that outcome and the balances that each sector records will be determined by a combination of their own spending decisions and the spillovers from the other sectors that impact on their respective incomes.

It also follows that it doesn’t matter how fast GDP is growing.

To refresh your memory the sectoral balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.

We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all taxes and transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).

Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).

Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):

(2) GNP = C + I + G + (X – M) + FNI

To render this approach into the sectoral balances form, we subtract total taxes and transfers (T) from both sides of Expression (3) to get:

(3) GNP – T = C + I + G + (X – M) + FNI – T

Now we can collect the terms by arranging them according to the three sectoral balances:

(4) (GNP – C – T) – I = (G – T) + (X – M + FNI)

The the terms in Expression (4) are relatively easy to understand now.

The term (GNP – C – T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.

The left-hand side of Equation (4), (GNP – C – T) – I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP – C – T).

In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.

The term (G – T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.

Finally, the other right-hand side term (X – M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.

In English we could say that:

The private financial balance equals the sum of the government financial balance plus the current account balance.

We can re-write Expression (6) in this way to get the sectoral balances equation:

(5) (S – I) = (G – T) + CAD

which is interpreted as meaning that government sector deficits (G – T > 0) and current account surpluses (CAD > 0) generate national income and net financial assets for the private domestic sector.

Conversely, government surpluses (G – T < 0) and current account deficits (CAD < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets.

Expression (5) can also be written as:

(6) [(S – I) – CAD] = (G – T)

where the term on the left-hand side [(S – I) – CAD] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance.

This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit).

The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers.

All these relationships (equations) hold as a matter of accounting and not matters of opinion.

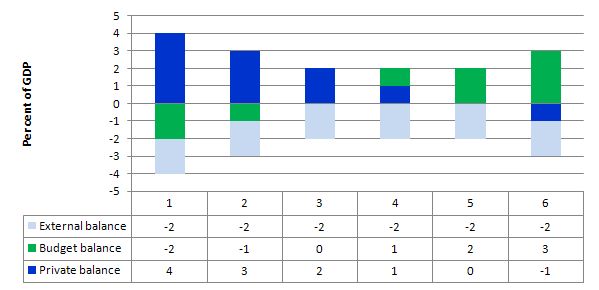
Consider the following graph and associated table of data which shows six states. All states have a constant external deficit equal to 2 per cent of GDP (light-blue columns).

State 1 show a government running a surplus equal to 2 per cent of GDP (green columns). As a consequence, the private domestic balance is in deficit of 4 per cent of GDP (royal-blue columns).

State 2 shows that when the fiscal surplus moderates to 1 per cent of GDP the private domestic deficit is reduced. State 3 is a fiscal balance and then the private domestic deficit is exactly equal to the external deficit. So the private sector spending more than they earn exactly funds the desire of the external sector to accumulate financial assets in the currency of issue in this country.

States 4 to 6 shows what happens when the fiscal balance goes into deficit – the private domestic sector (given the external deficit) can then start reducing its deficit and by State 5 it is in balance. Then by State 6 the private domestic sector is able to net save overall (that is, spend less than its income).

Note also that the government balance equals exactly $-for-$ (as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances). This is also a basic rule derived from the national accounts.

Most countries currently run external deficits. The crisis was marked by households reducing consumption spending growth to try to manage their debt exposure and private investment retreating. The consequence was a major spending gap which pushed the fiscal balance into deficits via the automatic stabilisers.

The only way to get income growth going in this context and to allow the private sector surpluses to build was to increase the deficits beyond the impact of the automatic stabilisers. The reality is that this policy change hasn’t delivered large enough fiscal deficits (even with external deficits narrowing). The result has been large negative income adjustments which brought the sectoral balances into equality at significantly lower levels of economic activity.

The following blogs may be of further interest to you:

• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!

Question 2:

Unlike a household which not only has to service its debt obligations over the course of the loan but also has to repay them at the due date, a national government debt, which issues its own currency can always roll over its “own currency” debt obligations and never has to pay them back.

The answer is False.

As a matter of clarification, note we are discussing debt issued in the currency of issue and not debt denominated in foreign currencies.

First, households do have to service their debts and repay them at some due date or risk default. The other crucial point is that households also have to forego some current consumption, use up savings or run down assets to service their debts and ultimately repay them.

Second, a sovereign government also has to service their debts and repay them at some due date or risk default. There is no difference there. The crucial difference is that unlike a household it does not have to forego any current spending capacity (or privatise public assets) to accomplish these financial transactions.

But the public debt is a legal obligation on government and so is a liability that has to be managed.

Now can it just roll-it over continuously? Well the question was subtle because the government can always keep issuing new debt when the old issues mature. But as the previous debt-issued matures it is paid out as per the terms of the issue.

The other point is that the liability on a sovereign government is legally like all liabilities – enforceable in courts the risk associated with taking that liability on is zero which is very different to the risks attached to taking on private debt.

There is zero financial risk that a holder of a public bond instrument will not be paid principle and interest on time.

The other point to appreciate is that the original holder of the public debt might not be the final holder who is paid out. The market for public debt is the most liquid of all debt markets and trading in public debt instruments of all nations is conducted across all markets each hour of every day.

While I am most familiar with the Australian institutional structure, the following developments are not dissimilar to the way bond issuance (in primary markets) is organised elsewhere. You can access information about this from the Australian Office of Financial Management, which is a Treasury-related public body that manages all public debt issuance in Australia.

It conducts the primary market, which is the institutional machinery via which the government sells debt to the non-government sector. In a modern monetary system with flexible exchange rates it is clear the government does not have to finance its spending so the fact that governments hang on to primary market issuance is largely ideological – fear of fiscal excesses rather than an intrinsic need. In this blog – Will we really pay higher interest rates? – I go into this period more fully and show that it was driven by the ideological calls for “fiscal discipline” and the growing influence of the credit rating agencies. Accordingly, all net spending had to be fully placed in the private market $-for-$. A purely voluntary constraint on the government and a waste of time.

A secondary market is where existing financial assets are traded by interested parties. So the financial assets enter the monetary system via the primary market and are then available for trading in the secondary. The same structure applies to private share issues for example. The company raises funds via the primary issuance process then its shares are traded in secondary markets.

Clearly secondary market trading has no impact at all on the volume of financial assets in the system – it just shuffles the wealth between wealth-holders. In the context of public debt issuance – the transactions in the primary market are vertical (net financial assets are created or destroyed) and the secondary market transactions are all horizontal (no new financial assets are created). Please read my blog – Deficit spending 101 – Part 3 – for more information.

Primary issues are conducted via auction tender systems and the Treasury determines the timing of these events in addition to the type and volumne of debt to be issued.

The issue is then be put out for tender and the market determines the final price of the bonds issued. Imagine a $A1000 bond is offered at a coupon of 5 per cent, meaning that you would get $A50 dollar per annum until the bond matured at which time you would get $A1000 back.

Imagine that the market wanted a yield of 6 per cent to accommodate risk expectations (see below). So for them the bond is unattractive unless the price is lower than $A1000. So tender system they would put in a purchase bid lower than the $A1000 to ensure they get the 6 per cent return they sought.

The general rule for fixed-income bonds is that when the prices rise, the yield falls and vice versa. Thus, the price of a bond can change in the market place according to interest rate fluctuations.

When interest rates rise, the price of previously issued bonds fall because they are less attractive in comparison to the newly issued bonds, which are offering a higher coupon rates (reflecting current interest rates).

When interest rates fall, the price of older bonds increase, becoming more attractive as newly issued bonds offer a lower coupon rate than the older higher coupon rated bonds.

So for new bond issues the AOFM receives the tenders from the bond market traders. These will be ranked in terms of price (and implied yields desired) and a quantity requested in $ millions. The AOFM (which is really just part of treasury) sometimes sells some bonds to the central bank (RBA) for their open market operations (at the weighted average yield of the final tender).

The AOFM will then issue the bonds in highest price bid order until it raises the revenue it seeks. So the first bidder with the highest price (lowest yield) gets what they want (as long as it doesn’t exhaust the whole tender, which is not likely). Then the second bidder (higher yield) and so on.

In this way, if demand for the tender is low, the final yields will be higher and vice versa. There are a lot of myths peddled in the financial press about this. Rising yields may indicate a rising sense of risk (mostly from future inflation although sovereign credit ratings will influence this). But they may also indicated a recovering economy where people are more confidence investing in commercial paper (for higher returns) and so they demand less of the “risk free” government paper.

So while there is no credit risk attached to holding public debt (that is, the holder knows they will receive the principle and interest that is specified on the issued debt instrument), there is still market risk which is related to movements in interest rates.

For government accounting purposes however the trading of the bonds once issued is of no consequence. They still retain the liability to pay the fixed coupon rate and the face value of the bond at the time of issue (not the market price).

The person/institution that sells the bond before maturity may gain or lose relative to their original purchase price but that is totally outside of the concern of the government.

Its liability is to pay the specified coupon rate at the time of issue and then the whole face value at the time of maturity.

There are complications to the primary sale process – some bonds sell at discounts which imply the coupon value. Further, there are arrangements between treasuries and central banks about the way in which public debt holdings are managed and accounted for. But these nuances do not alter the initial contention – public debt is a liability of the government in just the same way as private debt is a liability for those holders.

The following blogs may be of further interest to you:

• Time to outlaw the credit rating agencies
• Will we really pay higher interest rates?

Question 3:

Over the last two decades, there have been major redistributions of national income towards profits in many nations. This has occurred as a result of the suppression of real wages growth.

The answer is False.

The question suggests that there will be a redistribution of national income towards profits if the real wage falls. That is incorrect. There could be a redistribution towards wages even when the real wage falls.

And, further, a redistribution towards profits could occur even if the real wage rises.

In terms of the factor shares in national income we distinguish the wage share from the profit share. So for a redistribution of national income towards profits to occur the wage share has to fall.

The wage share in nominal GDP is expressed as the total wage bill as a percentage of nominal GDP. Economists differentiate between nomimal GDP ($GDP), which is total output produced at market prices and real GDP (GDP), which is the actual physical equivalent of the nominal GDP. We will come back to that distinction soon.

To compute the wage share we need to consider total labour costs in production and the flow of production ($GDP) each period.

Employment (L) is a stock and is measured in persons (averaged over some period like a month or a quarter or a year.

The wage bill is a flow and is the product of total employment (L) and the average wage (w) prevailing at any point in time. Stocks (L) become flows if it is multiplied by a flow variable (W). So the wage bill is the total labour costs in production per period.

So the wage bill = W.L

The wage share is just the total labour costs expressed as a proportion of $GDP – (W.L)/$GDP in nominal terms, usually expressed as a percentage. We can actually break this down further.

Labour productivity (LP) is the units of real GDP per person employed per period. Using the symbols already defined this can be written as:

LP = GDP/L

so it tells us what real output (GDP) each labour unit that is added to production produces on average.

We can also define another term that is regularly used in the media – the real wage – which is the purchasing power equivalent on the nominal wage that workers get paid each period. To compute the real wage we need to consider two variables: (a) the nominal wage (W) and the aggregate price level (P).

We might consider the aggregate price level to be measured by the consumer price index (CPI) although there are huge debates about that. But in a sense, this macroeconomic price level doesn’t exist but represents some abstract measure of the general movement in all prices in the economy.

Macroeconomics is hard to learn because it involves these abstract variables that are never observed – like the price level, like “the interest rate” etc. They are just stylisations of the general tendency of all the different prices and interest rates.

Now the nominal wage (W) – that is paid by employers to workers is determined in the labour market – by the contract of employment between the worker and the employer. The price level (P) is determined in the goods market – by the interaction of total supply of output and aggregate demand for that output although there are complex models of firm price setting that use cost-plus mark-up formulas with demand just determining volume sold. We shouldn’t get into those debates here.

The inflation rate is just the continuous growth in the price level (P). A once-off adjustment in the price level is not considered by economists to constitute inflation.

So the real wage (w) tells us what volume of real goods and services the nominal wage (W) will be able to command and is obviously influenced by the level of W and the price level. For a given W, the lower is P the greater the purchasing power of the nominal wage and so the higher is the real wage (w).

We write the real wage (w) as W/P. So if W = 10 and P = 1, then the real wage (w) = 10 meaning that the current wage will buy 10 units of real output. If P rose to 2 then w = 5, meaning the real wage was now cut by one-half.

Nominal GDP ($GDP) can be written as P.GDP, where the P values the real physical output.

Now if you put of these concepts together you get an interesting framework. To help you follow the logic here are the terms developed and be careful not to confuse $GDP (nominal) with GDP (real):

• Wage share = (W.L)/$GDP
• Nominal GDP: $GDP = P.GDP
• Labour productivity: LP = GDP/L
• Real wage: w = W/P

By substituting the expression for Nominal GDP into the wage share measure we get:

Wage share = (W.L)/P.GDP

In this area of economics, we often look for alternative way to write this expression – it maintains the equivalence (that is, obeys all the rules of algebra) but presents the expression (in this case the wage share) in a different “view”.

So we can write as an equivalent:

Wage share – (W/P).(L/GDP)

Now if you note that (L/GDP) is the inverse (reciprocal) of the labour productivity term (GDP/L). We can use another rule of algebra (reversing the invert and multiply rule) to rewrite this expression again in a more interpretable fashion.

So an equivalent but more convenient measure of the wage share is:

Wage share = (W/P)/(GDP/L) – that is, the real wage (W/P) divided by labour productivity (GDP/L).

I won’t show this but I could also express this in growth terms such that if the growth in the real wage equals labour productivity growth the wage share is constant. The algebra is simple but we have done enough of that already.

That journey might have seemed difficult for those not well-versed in simple algebra but it produces a very easy to understand formula for the wage share.

Two other points to note. The wage share is also equivalent to the real unit labour cost (RULC) measures that Treasuries and central banks use to describe trends in costs within the economy. Please read my blog – Saturday Quiz – May 15, 2010 – answers and discussion – for more discussion on this point.

Now it becomes obvious that if the nominal wage (W) and the price level (P) are growing at the pace the real wage is constant. And if the real wage is growing at the same rate as labour productivity, then both terms in the wage share ratio are equal and so the wage share is constant.

The wage share was constant for a long time during the Post Second World period and this constancy was so marked that Kaldor (the Cambridge economist) termed it one of the great “stylised” facts. So real wages grew in line with productivity growth which was the source of increasing living standards for workers.

The productivity growth provided the “room” in the distribution system for workers to enjoy a greater command over real production and thus higher living standards without threatening inflation.

Since the mid-1980s, the neo-liberal assault on workers’ rights (trade union attacks; deregulation; privatisation; persistently high unemployment) has seen this nexus between real wages and labour productivity growth broken. So while real wages have been stagnant or growing modestly, this growth has been dwarfed by labour productivity growth.

So if the real wage is falling and productivity growth is positive or at least not falling as fast as the real wage, then there will be a redistribution of national income towards profits.

The following blogs may be of further interest to you:

• A radical redistribution of income undermined US entrepreneurship
• Saturday Quiz – May 15, 2010 – answers and discussion
• The origins of the economic crisis

That is enough for today!

(c) Copyright 2018 William Mitchell. All Rights Reserved.