The Weekend Quiz – September 3-4, 2016 – answers and discussion

Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

Modern Monetary Theory (MMT) recognises the potential problem with running continuous fiscal deficits is that the spending builds up over time which adds to inflationary pressures.

The answer is False.

This question tests whether you understand that fiscal deficits are just the outcome of two flows which have a finite lifespan. Flows typically feed into stocks (increase or decrease them) and in the case of deficits, under current institutional arrangements, they increase public debt holdings.

So the expenditure impacts of deficit exhaust each period and underpin production and income generation and saving. Aggregate saving is also a flow but can add to stocks of financial assets when stored.

As long as the flow of net spending from the public sector is consistent with filling the non-government spending gap then a nation can absorb continuous fiscal deficits without inflationary pressures building.

Under current institutional arrangements (where governments unnecessarily issue debt to match its net spending $-for-$) the deficits will also lead to a rise in the stock of public debt outstanding. But of-course, the increase in debt is not a consequence of any “financing” imperative for the government. A sovereign government is never revenue constrained because it is the monopoly issuer of the currency.

The following blogs may be of further interest to you:

• Deficit spending 101 – Part 1
• Deficit spending 101 – Part 2
• Deficit spending 101 – Part 3
• Fiscal sustainability 101 – Part 1
• Fiscal sustainability 101 – Part 2
• Fiscal sustainability 101 – Part 3

Question 2:

In recent months, we have observed falling government bond yields in most nations which suggests that investors are viewing sovereign debt less favourably as the levels of outstanding debt rises.

The answer is False.

In macroeconomics, we summarise the plethora of public debt instruments with the concept of a bond. The standard bond has a face value – say $1000 and a coupon rate – say 5 per cent and a maturity – say 10 years. This means that the bond holder will will get $50 dollar per annum (interest) for 10 years and when the maturity is reached they would get $1000 back.

Bonds are issued by government into the primary market, which is simply the institutional machinery via which the government sells debt to “raise funds”. In a modern monetary system with flexible exchange rates it is clear the government does not have to finance its spending so the the institutional machinery is voluntary and reflects the prevailing neo-liberal ideology – which emphasises a fear of fiscal excesses rather than any intrinsic need.

Once bonds are issued they are traded in the secondary market between interested parties. Clearly secondary market trading has no impact at all on the volume of financial assets in the system – it just shuffles the wealth between wealth-holders. In the context of public debt issuance – the transactions in the primary market are vertical (net financial assets are created or destroyed) and the secondary market transactions are all horizontal (no new financial assets are created). Please read my blog – Deficit spending 101 – Part 3 – for more discussion on this point.

Further, most primary market issuance is now done via auction. Accordingly, the government would determine the maturity of the bond (how long the bond would exist for), the coupon rate (the interest return on the bond) and the volume (how many bonds) being specified.

The issue would then be put out for tender and the market then would determine the final price of the bonds issued. Imagine a $1000 bond had a coupon of 5 per cent, meaning that you would get $50 dollar per annum until the bond matured at which time you would get $1000 back.

Imagine that the market wanted a yield of 6 per cent to accommodate risk expectations (inflation or something else). So for them the bond is unattractive and they would avoid it under the tap system. But under the tender or auction system they would put in a purchase bid lower than the $1000 to ensure they get the 6 per cent return they sought.

The mathematical formulae to compute the desired (lower) price is quite tricky and you can look it up in a finance book.

The general rule for fixed-income bonds is that when the prices rise, the yield falls and vice versa. Thus, the price of a bond can change in the market place according to interest rate fluctuations.

When interest rates rise, the price of previously issued bonds fall because they are less attractive in comparison to the newly issued bonds, which are offering a higher coupon rates (reflecting current interest rates).

When interest rates fall, the price of older bonds increase, becoming more attractive as newly issued bonds offer a lower coupon rate than the older higher coupon rated bonds.

Further, falling yields indicate that the demand for bonds is rising which suggests that investors are viewing them more favourably (relative to other investment products).

The following blogs may be of further interest to you:

• Saturday Quiz – April 17, 2010 – answers and discussion
• Time to outlaw the credit rating agencies
• Studying macroeconomics – an exercise in deception
• Time for a reality check on debt – Part 1
• Will we really pay higher interest rates?

Question 3:

If private domestic investment is less than private domestic saving, and the external sector is draining aggregate spending from the domestic economy, then the government fiscal balance has to be in deficit no matter what level of GDP is produced.

The answer is True.

This question requires an understanding of the sectoral balances that can be derived from the National Accounts. But it also requires some understanding of the behavioural relationships within and between these sectors which generate the outcomes that are captured in the National Accounts and summarised by the sectoral balances.

To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

(1) GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.

We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all tax revenue minus total transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).

Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).

Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):

(2) GNP = C + I + G + (X – M) + FNI

To render this approach into the sectoral balances form, we subtract total net taxes (T) from both sides of Expression (3) to get:

(3) GNP – T = C + I + G + (X – M) + FNI – T

Now we can collect the terms by arranging them according to the three sectoral balances:

(4) (GNP – C – T) – I = (G – T) + (X – M + FNI)

The the terms in Expression (4) are relatively easy to understand now.

The term (GNP – C – T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.

The left-hand side of Equation (4), (GNP – C – T) – I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP – C – T).

In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.

The term (G – T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.

Finally, the other right-hand side term (X – M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.

In English we could say that:

The private financial balance equals the sum of the government financial balance plus the current account balance.

We can re-write Expression (6) in this way to get the sectoral balances equation:

(5) (S – I) = (G – T) + CAD

which is interpreted as meaning that government sector deficits (G – T > 0) and current account surpluses (CAD > 0) generate national income and net financial assets for the private domestic sector.

Conversely, government surpluses (G – T < 0) and current account deficits (CAD < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets.

Expression (5) can also be written as:

(6) [(S – I) – CAD] = (G – T)

where the term on the left-hand side [(S – I) – CAD] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance.

This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit).

The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers.

All these relationships (equations) hold as a matter of accounting and not matters of opinion.

So what about the situation posed in the question?

If the external sector is draining aggregate demand it must mean the current account is in deficit. That is , spending flows out of the local economy are greater than spending flows coming into the economy from the foreign sector.

If private domestic investment is less than private domestic saving, then the private domestic sector is running a surplus overall – that is, they are spending less than they are earning.

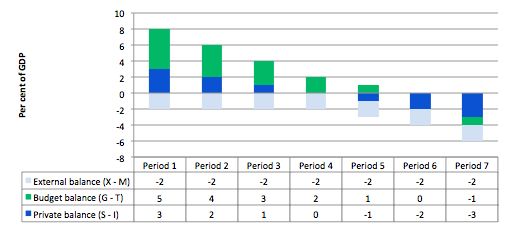
The following graph shows the sectoral balances for seven periods based on different levels of the private balance (as a per cent of GDP) and a constant external deficit (to keep things simple).

You can see that in Periods 1 to 3, the private sector is in surplus while the external sector is in deficit. The fiscal balance (G – T) is in deficit in each of those periods. The fiscal balance only goes into surplus (with a 2 per cent of GDP external deficit) when the injection into aggregate demand from the private domestic sector is greater than the spending drain from the external sector (Period 7).

The reasoning is as follows. If the private domestic sector (households and firms) is saving overall it means that some of the income being produced is not be re-spent. So the private domestic surplus represents a drain on aggregate demand. The external sector is also leaking expenditure. At the current GDP level, if the government didn’t fill the spending gap resulting from the other sectors, then inventories would start to increase beyond the desired level of the firms.

The firms would react to the increased inventory holding costs and would cut back production. How quickly this downturn occurs would depend on a number of factors including the pace and magnitude of the initial demand contraction. But the result would be that the economy would contract – output, employment and income would all fall.

The initial contraction in consumption would multiply through the expenditure system as laid-off workers lose income and cut back on their spending. This would lead to further contractions.

Declining national income (GDP) leads to a number of consequences. Net exports improve as imports fall (less income) but the question clearly assumes that the external sector remains in deficit. Total saving actually starts to decline as income falls as does induced consumption.

The decline in income then stifles firms’ investment plans – they become pessimistic of the chances of realising the output derived from augmented capacity and so aggregate demand plunges further. Both these effects push the private domestic balance further into surplus

With the economy in decline, tax revenue falls and welfare payments rise which push the public fiscal balance towards and eventually into deficit via the automatic stabilisers.

So with an external deficit and a private domestic surplus there will always be a fiscal deficit.

The following blogs may be of further interest to you:

• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!