Saturday Quiz – January 25, 2014 – answers and discussion

Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of modern monetary theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

If the household saving ratio and/or the nation’s external deficit rises, there is no necessity for the government deficit to rise in order to maintain current output growth.

The answer is True.

This question tests one’s basic understanding of the sectoral balances that can be derived from the National Accounts. The secret to getting the correct answer is to realise that the household saving ratio is not the overall sectoral balance for the private domestic sector.

In other words, if you just compared the household saving ratio with the external deficit and the budget balance you would be leaving an essential component of the private domestic balance out – private capital formation (investment).

To understand that, in macroeconomics we have a way of looking at the national accounts (the expenditure and income data) which allows us to highlight the various sectors – the government sector and the non-government sector (and the important sub-sectors within the non-government sector).

So we start by focusing on the final expenditure components of consumption (C), investment (I), government spending (G), and net exports (exports minus imports) (NX).

The basic aggregate demand equation in terms of the sources of spending is:

GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

In terms of the uses that national income (GDP) can be put too, we say:

GDP = C + S + T

which says that GDP (income) ultimately comes back to households who consume, save (S) or pay taxes (T) with it once all the distributions are made.

So if we equate these two ideas sources of GDP and uses of GDP, we get:

C + S + T = C + I + G + (X – M)

Which we then can simplify by cancelling out the C from both sides and re-arranging (shifting things around but still satisfying the rules of algebra) into what we call the sectoral balances view of the national accounts.

There are three sectoral balances derived – the Budget Deficit (G – T), the Current Account balance (X – M) and the private domestic balance (S – I).

These balances are usually expressed as a per cent of GDP but we just keep them in $ values here:

(S – I) = (G – T) + (X – M)

The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.

You can then manipulate these balances to tell stories about what is going on in a country.

For example, when an external deficit (X – M < 0) and a public surplus (G - T < 0) coincide, there must be a private deficit. So if X = 10 and M = 20, X - M = -10 (a current account deficit). Also if G = 20 and T = 30, G - T = -10 (a budget surplus). So the right-hand side of the sectoral balances equation will equal (20 - 30) + (10 - 20) = -20. As a matter of accounting then (S - I) = -20 which means that the domestic private sector is spending more than they are earning because I > S by 20 (whatever $ units we like). So the fiscal drag from the public sector is coinciding with an influx of net savings from the external sector. While private spending can persist for a time under these conditions using the net savings of the external sector, the private sector becomes increasingly indebted in the process. It is an unsustainable growth path.

So if a nation usually has a current account deficit (X – M < 0) then if the private domestic sector is to net save (S - I) > 0, then the public budget deficit has to be large enough to offset the current account deficit. Say, (X – M) = -20 (as above). Then a balanced budget (G – T = 0) will force the domestic private sector to spend more than they are earning (S – I) = -20. But a government deficit of 25 (for example, G = 55 and T = 30) will give a right-hand solution of (55 – 30) + (10 – 20) = 15. The domestic private sector can net save.

So by only focusing on the household saving ratio in the question, I was only referring to one component of the private domestic balance. Clearly in the case of the question, if private investment is strong enough to offset the household desire to increase saving (and withdraw from consumption) then no spending gap arises.

In the present situation in most countries, households have reduced the growth in consumption (as they have tried to repair overindebted balance sheets) at the same time that private investment has fallen dramatically.

As a consequence a major spending gap emerged that could only be filled in the short- to medium-term by government deficits if output growth was to remain intact. The reality is that the budget deficits were not large enough and so income adjustments (negative) occurred and this brought the sectoral balances in line at lower levels of economic activity.

In all likelihood, however, given that investment spending is unlikely to respond quickly, there would probably be a need to increase government net spending – but it isn’t necessarily the case.

The following blogs may be of further interest to you:

• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!

Question 2:

A nation experiences growth in total employment in a particular month in net terms, rising unemployment, and a marginal decline in the labour force participation rate. Taken together this information tells you that:

(a) Labour force growth outstripped employment growth but was less than the growth in the working age population.

(b) The working age population grew faster than employment and offset the decline in the labour force arising from the drop in the participation rate.

(c) The labour force grew faster than employment but you cannot tell what happened to the working age population from the information provided.

The answer is Option (a) Labour force growth outstripped employment growth but was less than the growth in the working age population..

If you didn’t get this correct then it is likely you lack an understanding of the labour force framework which is used by all national statistical offices.

The labour force framework is the foundation for cross-country comparisons of labour market data. The framework is made operational through the International Labour Organization (ILO) and its International Conference of Labour Statisticians (ICLS). These conferences and expert meetings develop the guidelines or norms for implementing the labour force framework and generating the national labour force data.

The rules contained within the labour force framework generally have the following features:

• an activity principle, which is used to classify the population into one of the three basic categories in the labour force framework;
• a set of priority rules, which ensure that each person is classified into only one of the three basic categories in the labour force framework; and
• a short reference period to reflect the labour supply situation at a specified moment in time.

The system of priority rules are applied such that labour force activities take precedence over non-labour force activities and working or having a job (employment) takes precedence over looking for work (unemployment). Also, as with most statistical measurements of activity, employment in the informal sectors, or black-market economy, is outside the scope of activity measures.

Paid activities take precedence over unpaid activities such that for example ‘persons who were keeping house’ as used in Australia, on an unpaid basis are classified as not in the labour force while those who receive pay for this activity are in the labour force as employed.

Similarly persons who undertake unpaid voluntary work are not in the labour force, even though their activities may be similar to those undertaken by the employed. The category of ‘permanently unable to work’ as used in Australia also means a classification as not in the labour force even though there is evidence to suggest that increasing ‘disability’ rates in some countries merely reflect an attempt to disguise the unemployment problem.

The following diagram shows the complete breakdown of the categories used by the statisticians in this context. The yellow boxes are relevant for this question.

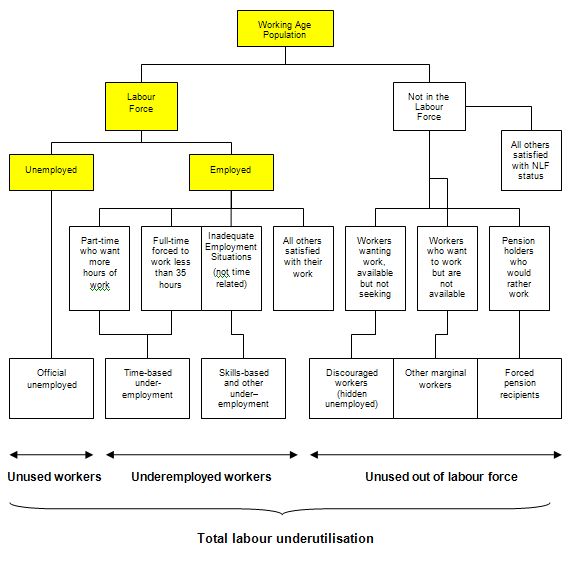
So the Working Age Population (WAP) is usually defined as those persons aged between 15 and 65 years of age or increasing those persons above 15 years of age (recognising that official retirement ages are now being abandoned in many countries).

As you can see from the diagram the WAP is then split into two categories: (a) the Labour Force (LF) and; (b) Not in the Labour Force – and this divisision is based on activity tests (being in paid employed or actively seeking and being willing to work).

The Labour Force Participation Rate is the percentage of the WAP that are active. So if the participation rate is 65 per cent it means that 65 per cent of those persons above the age of 15 are actively engaged in the labour market (either employed or unemployed).

You can also see that the Labour Force is divided into employment and unemployment. Most nations use the standard demarcation rule that if you have worked for one or more hours a week during the survey week you are classified as being employed.

If you are not working but indicate you are actively seeking work and are willing to currently work then you are considered to be unemployed. If you are not working and indicate either you are not actively seeking work or are not willing to work currently then you are considered to be Not in the Labour Force.

So you get the category of hidden unemployed who are willing to work but have given up looking because there are no jobs available. The statistician counts them as being outside the labour force even though they would accept a job immediately if offered.

The question gave you information about employment, unemployment and the labour force participation rate and you had to deduce the rest based on your understanding.

In terms of the Diagram the following formulas link the yellow boxes:

Labour Force = Employment + Unemployment = Labour Force Participation Rate times the Working Age Population

It follows that the Working Age Population is derived as Labour Force divided by the Labour Force Participation Rate (appropriately scaled in percentage point units).

So if both Employment and Unemployment is growing then you can conclude that the Labour Force is growing by the sum of the extra Employment and Unemployment expressed as a percentage of the previous Labour Force.

The Labour Force can grow in one of four ways:

• Working Age Population growing with the labour force participation rate constant;
• Working Age Population growing and offsetting a falling labour force participation rate;
• Working Age Population constant and the labour force participation rate rising;
• Working Age Population falling but being offset by a rising labour force participation rate.

So in our case, if the Participation Rate is falling then the proportion of the Working Age Population that is entering the Labour Force is falling. So for the Labour Force to be growing the Working Age Population has to be growing faster than the Labour Force.

Now consider the following Table which shows the Australian labour force aggregates for January and February 2010 (the same that were used in the question).

So the correct answer is as above.

Of the second option:

The working age population grew faster than employment and offset the decline in the labour force arising from the drop in the participation rate.

Clearly impossible if both employment and unemployment both rose.

And of the third option:

The labour force grew faster than employment but you cannot tell what happened to the working age population from the information provided.

Clearly you can tell what happened to the working age population by deduction.

The following blog may be of further interest to you:

• Being beguiled by labour force data

Question 3:

If Brussels relaxed the budget restrictions on national governments that are applicable under the Stability and Growth Pact (3 per cent deficit to GDP ratios and 60 per cent public debt to GDP ratios) then the current solvency risk facing several EMU members would be resolved.

The answer is False.

Linking of solvency risk and the Stability and Growth Pact is false.

The Stability and Growth Pact which is summarised as imposing a rule on EMU member countries that their budget deficits cannot exceed 3 per cent of GDP rule and their public debt to GDP ratio cannot exceed 60 per cent. In the links provided below you will find extensive analysis of the nonsensical nature of these rules.

The SGP was designed to place nationally-determined fiscal policy in a straitjacket to avoid the problems that would arise if some runaway member states might follow a reckless spending policy, which in its turn would force the ECB to increase its interest rates. Germany, in particular, wanted fiscal constraints put on countries like Italy and Spain to prevent reckless government spending which could damage compliant countries through higher ECB interest rates.

In a 2006 book I published with Joan Muysken and Tom Van Veen – Growth and cohesion in the European Union: The Impact of Macroeconomic Policy – we showed that it is widely recognised that these figures were highly arbitrary and were without any solid theoretical foundation or internal consistency.

The current crisis is just the last straw in the myth that the SGP would provide a platform for stability and growth in the EMU. In my 2008 book (published just before the crisis) with Joan Muysken – Full Employment abandoned – we provided evidence to support the thesis that the SGP failed on both counts – it had provided neither stability nor growth. The crisis has echoed that claim very loudly.

The rationale of controlling government debt and budget deficits were consistent with the rising neo-liberal orthodoxy that promoted inflation control as the macroeconomic policy priority and asserted the primacy of monetary policy (a narrow conception notwithstanding) over fiscal policy. Fiscal policy was forced by this inflation first ideology to become a passive actor on the macroeconomic stage.

But these rules, while ensuring that the EMU countries will have to live with high unemployment and depressed living standards (overall) for years to come, given the magnitude of the crisis and the austerity plans that have to be pursued to get the public ratios back in line with the SGP dictates, are not the reason that the EMU countries risk insolvency.

That risk arises from the fact that when they entered the EMU system, they ceded their currency sovereignty to the European Central Bank (ECB) which had several consequences. First, EMU member states now share a common monetary stance and cannot set interest rates independently. The former central banks – now called National Central Banks are completely embedded into the ECB-NCB system that defines the EMU.

Second, they no longer have separate exchange rates which means that trade imbalances have to be dealt with in monetary terms not in relative price changes.

Third, and most importantly, the member governments cannot create their own currency and as a consequence can run out of Euros! So imagine there was a bank run occuring in Australia, while the situation would signal mass frenzy, the Australian government has the infinite capacity to guarantee all deposits denominated in $AUD should it choose to do so. If the superannuation industry collapsed in Australia, the Australian government could just guarantee all retirement incomes denominated in $AUD should it choose to do so. The same goes for any sovereign government (including the US and the UK).

But an EMU member government could not do this and their banking or public pension systems could become insolvent.

Further, it could reach a situation where it did not have enough Euros available (via taxation revenue or borrowing) to repay its debt commitments (either retire existing debt on maturity or service interest payments). In that sense, the government itself would become insolvent.

A sovereign government such as Australia or the US could never find itself in that sort of situation – they are never in risk of insolvency.

So the source of the solvency risk problem is not the fiscal rules that the EMU nations have placed on themselves but the fact they have ceded currency sovereignty.

The following blogs may be of further interest to you:

• Euro zone’s self-imposed meltdown
• A Greek tragedy …
• España se está muriendo
• Exiting the Euro?
• Doomed from the start
• Europe – bailout or exit?
• Not the EMF … anything but the EMF!