Saturday Quiz – July 27, 2013 – answers and discussion

Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

The data shows that the private domestic sector in a nation with a very small external deficit (as a % of GDP) is spending less than it earns. However, you cannot tell what the government budget balance will be as a percentage of GDP until you know whether the external balance offsets the private domestic balance.

The answer is False.

This question requires an understanding of the sectoral balances that can be derived from the National Accounts. But it also requires some understanding of the behavioural relationships within and between these sectors which generate the outcomes that are captured in the National Accounts and summarised by the sectoral balances.

Refreshing the balances – we know that from an accounting sense, if the external sector overall is in deficit, then it is impossible for both the private domestic sector and government sector to run surpluses. One of those two has to also be in deficit to satisfy the accounting rules.

The important point is to understand what behaviour and economic adjustments drive these outcomes.

The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

From the uses perspective, national income (GDP) can be used for:

GDP = C + S + T

which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.

Equating these two perspectives we get:

C + S + T = GDP = C + I + G + (X – M)

So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.

(I – S) + (G – T) + (X – M) = 0

That is the three balances have to sum to zero. The sectoral balances derived are:

• The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
• The Budget Deficit (G – T) – negative if in surplus, positive if in deficit.
• The Current Account balance (X – M) – positive if in surplus, negative if in deficit.

These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.

A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).

This is also a basic rule derived from the national accounts and has to apply at all times.

So what economic behaviour might lead to the outcome specified in the question?

If the nation is running an external deficit it means that the contribution to aggregate demand from the external sector is negative – that is net drain of spending – dragging output down. The reference to a “small” external deficit was to place doubt in your mind. In fact, it doesn’t matter how large the external deficit is for this question.

Assume, now that the private domestic sector (households and firms) seeks to increase its overall saving (that is, spend less than it earns) and is successful in doing so. Consistent with this aspiration, households may cut back on consumption spending and save more out of disposable income. The immediate impact is that aggregate demand will fall and inventories will start to increase beyond the desired level of the firms.

The firms will soon react to the increased inventory holding costs and will start to cut back production. How quickly this happens depends on a number of factors including the pace and magnitude of the initial demand contraction. But if the households persist in trying to save more and consumption continues to lag, then soon enough the economy starts to contract – output, employment and income all fall.

The initial contraction in consumption multiplies through the expenditure system as workers who are laid off also lose income and their spending declines. This leads to further contractions.

The declining income leads to a number of consequences. Net exports improve as imports fall (less income) but the question clearly assumes that the external sector remains in deficit. Total saving actually starts to decline as income falls as does induced consumption.

So the initial discretionary decline in consumption is supplemented by the induced consumption falls driven by the multiplier process.

The decline in income then stifles firms’ investment plans – they become pessimistic of the chances of realising the output derived from augmented capacity and so aggregate demand plunges further. Both these effects push the private domestic balance further towards and eventually into surplus

With the economy in decline, tax revenue falls and welfare payments rise which push the public budget balance towards and eventually into deficit via the automatic stabilisers.

If the private sector persists in trying to net save then the contracting income will clearly push the budget into deficit.

So we would have an external deficit, a private domestic surplus and a budget deficit.

There will always be a budget deficit at any national income level, if the private domestic sector is succeessfully spending less than it earns and the external sector is in deficit.

The following blogs may be of further interest to you:

• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!

Question 2:

Modern Monetary Theory (MMT) observes that the private sector is wealthier if a currency-issuing government matches its deficit spending with bond issues relative to a situation where the government maintained the same size deficits without issuing bonds to the private sector.

The answer is False.

This answer relies on an understanding the banking operations that occur when governments spend and issue debt within a fiat monetary system. That understanding allows us to appreciate what would happen if a sovereign, currency-issuing government (with a flexible exchange rate) ran a budget deficit without issuing debt?

In this situation, like all government spending, the Treasury would credit the reserve accounts held by the commercial bank at the central bank. The commercial bank in question would be where the target of the spending had an account. So the commercial bank’s assets rise and its liabilities also increase because a deposit would be made.

The transactions are clear: The commercial bank’s assets rise and its liabilities also increase because a new deposit has been made. Further, the target of the fiscal initiative enjoys increased assets (bank deposit) and net worth (a liability/equity entry on their balance sheet). Taxation does the opposite and so a deficit (spending greater than taxation) means that reserves increase and private net worth increases.

This means that there are likely to be excess reserves in the “cash system” which then raises issues for the central bank about its liquidity management. The aim of the central bank is to “hit” a target interest rate and so it has to ensure that competitive forces in the interbank market do not compromise that target.

When there are excess reserves there is downward pressure on the overnight interest rate (as banks scurry to seek interest-earning opportunities), the central bank then has to sell government bonds to the banks to soak the excess up and maintain liquidity at a level consistent with the target. Some central banks offer a return on overnight reserves which reduces the need to sell debt as a liquidity management operation.

What would happen if there were bond sales? All that happens is that the banks reserves are reduced by the bond sales but this does not reduce the deposits created by the net spending. So net worth is not altered. What is changed is the composition of the asset portfolio held in the non-government sector.

The only difference between the Treasury “borrowing from the central bank” and issuing debt to the private sector is that the central bank has to use different operations to pursue its policy interest rate target. If it debt is not issued to match the deficit then it has to either pay interest on excess reserves (which most central banks are doing now anyway) or let the target rate fall to zero (the Japan solution).

There is no difference to the impact of the deficits on net worth in the non-government sector.

Mainstream economists would say that by draining the reserves, the central bank has reduced the ability of banks to lend which then, via the money multiplier, expands the money supply.

However, the reality is that:

• Building bank reserves does not increase the ability of the banks to lend.
• The money multiplier process so loved by the mainstream does not describe the way in which banks make loans.
• Inflation is caused by aggregate demand growing faster than real output capacity. The reserve position of the banks is not functionally related with that process.

So the banks are able to create as much credit as they can find credit-worthy customers to hold irrespective of the operations that accompany government net spending.

You may wish to read the following blogs for more information:

• Why history matters
• Building bank reserves will not expand credit
• Building bank reserves is not inflationary
• The complacent students sit and listen to some of that
• Saturday Quiz – February 27, 2010 – answers and discussion

Question 3

In Year 1, the economy plunges into recession with nominal GDP growth falling to minus -1 per cent. The inflation rate is subdued at 2 per cent per annum. The outstanding public debt is equal to the value of the nominal GDP and the nominal interest rate is equal to 2 per cent (and this is the rate the government pays on all outstanding debt). The government’s budget balance net of interest payments goes into deficit equivalent to 1 per cent of GDP and the debt ratio rises by 4 per cent. In Year 2, the government introduces a fiscal stimulus and pushes the primary budget deficit out to 3 per cent of GDP to head of a recession. In doing so it stimulates aggregate demand and nominal GDP growth rises to 4 per cent nominal GDP growth rate. The central bank holds the nominal interest rate constant and inflation is stable. In Year 3, there is no change in monetary policy, and the government expands fiscal policy by an additional 1 per cent of GDP. Inflation is stable and nominal GDP growth rises to 6 per cent. From this data, you can conclude that:

(a) The debt ratio rises in Years 2 and 3 but the size of the increase (in percentage points) diminishes in the third year.

(b) The debt ratio rises in Year 2 but by the end of Year 3, it is lower than it was at the start of Year 1.

(c) The debt ratio progressively falls over the two years.

The answer is Option (a).

This question requires you to understand the key parameters and relationships that determine the dynamics of the public debt ratio. An understanding of these relationships allows you to debunk statements that are made by those who think fiscal austerity will allow a government to reduce its public debt ratio or that fiscal stimulus will blow the public debt ratio out.

While Modern Monetary Theory (MMT) places no particular importance in the public debt to GDP ratio for a sovereign government, given that insolvency is not an issue, the fact remains that in the case of the Eurozone nations there is a funding issue and so debt ratios do matter.

Each Eurozone nation has to fund its spending because of the simple fact that it surrendered its currency sovereignty the day it agreed to use a foreign currency – the Euro.

It can either fund from taxation revenue or bond-issuance on a sustainable basis. The bond markets know that each nation (Germany included) carries solvency risk although the practical extent of that risk varies significantly across the member nations and that variation is largely reflected in the differential bond yields.

A primary budget balance is the difference between government spending (excluding interest rate servicing) and taxation revenue.

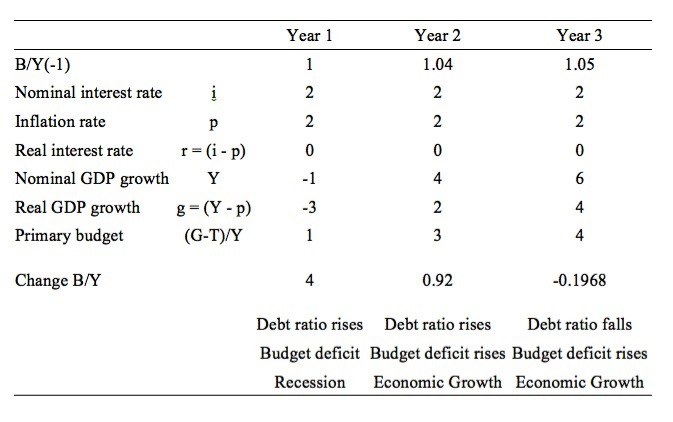
The following equation shows the change in the public debt ratio (Δ B/Y):

The symbol, Δ is the Greek for change.

In English, this says that the change in the debt ratio is the sum of two terms on the right-hand side: (a) the difference between the real interest rate (r) and the real GDP growth rate (g) times the initial debt ratio; and (b) the ratio of the primary deficit (G-T) to GDP.

The real interest rate is the difference between the nominal interest rate and the inflation rate. Real GDP is the nominal GDP deflated by the inflation rate. So the real GDP growth rate is equal to the Nominal GDP growth minus the inflation rate.

The formula can easily demonstrate that a nation running a primary deficit can reduce its public debt ratio over time.

Furthermore, depending on contributions from the external sector, a nation running a deficit will more likely create the conditions for a reduction in the public debt ratio than a nation that introduces an austerity plan aimed at running primary surpluses.

But if growth is not sufficient then the public debt ratio can rise.

Here is why that is the case. While a growing economy can absorb more debt and keep the debt ratio constant or falling an increasing real interest rate also means that interest payments on the outstanding stock of debt rise.

From the formula above, if the primary budget balance is zero, public debt increases at a rate r but the public debt ratio increases at r – g.

So do some arithmetic to ensure you understand this. Refer to the Table below which shows the calculations.

Start by assuming a public debt ratio at the start of the Year 1 of 100 per cent (so B/Y(-1) = 1) which means that outstanding public debt is equal to the value of the nominal GDP. In the public debate a public debt ratio of 100 per cent would be very large and invoke all sorts of claims about solvency and persistently negative growth (the Spreadsheet Experts!).

If we also assume that in the current year (Year 1) that the nominal interest rate is 2 per cent and the inflation rate is 2 per cent then the current real interest rate (r) is 0 per cent.

If the nominal GDP grows at -1 per cent and there is an inflation rate of 2 per cent then real GDP is growing (g) at minus 3 per cent.

Under these conditions, the primary budget surplus would have to be equal to 3 per cent of GDP to stabilise the debt ratio (check it for yourself).

In Year 1, the primary budget deficit is actually 1 per cent of GDP so we know by computation that the public debt ratio rises by 4 per cent.

The calculation (using the formula in the Table) is:

Change in B/Y = (0 – (-3))*1 + 1 = 4 per cent.

In Year 2, monetary policy is unchanged and inflation is stable so the real interest rate remains at zero per cent.

From the Table below, note that the public debt ratio at the beginning of the period has risen to 1.04 because of the 4 per cent rise from Year 1.

The primary budget balance (deficit) rises to 3 per cent of GDP and nominal GDP growth recovers quickly and rises to 4 per cent, which means real GDP growth (given the inflation rate) is equal to 2 per cent.

The corresponding calculation for the change in the public debt ratio in Year 2 is:

Change in B/Y = (0 – 2)*1.04 + 3 = 0.92 per cent.

That is, the public debt ratio rises but at a slower rate than in the last year. The real growth in the economy has been beneficial and if maintained would start to eat into the primary budget balance (via the rising tax revenues that would occur).

In Year 3, real interest rate is zero, nominal GDP growth rises to 6 per cent (real GDP growth is 4 per cent) on the back of a rising primary budget deficit of 4 per cent.

The sustained growth leads to a reduction in the public debt ratio of 0.001968 percentage points, and the ratio at the beginning of Year 4 would be 1.0472 (104.72 per cent).

In a few years, the growth would also start to reduce the primary budget deficit as tax revenue rose and government maintained stable tax rates and spending growth rates.

The best way to reduce the public debt ratio is to stop issuing debt but that would require a dismantling of the Eurozone – a thoroughly recommended option.

But irrespective of that nuance, governments should go for growth and use expansionary deficits as the growth engine and then all the financial ratios that people worry about will take care of themselves.