The Weekend Quiz – August 24-25, 2019 – answers and discussion

Here are the answers with discussion for this Weekend’s Quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

A fiscal deficit equivalent to 3 per cent of GDP signals that the government is having a less expansionary impact than if the fiscal deficit outcome was equivalent to 5 per cent of GDP.

The answer is True.

The question probes an understanding of the forces (components) that drive the fiscal balance that is reported by government agencies at various points in time. Note the question is not about the policy intent, which would have made Option (c) correct. The question is about the absolute impact of the government policy stance which includes its discretionary policy choices and the cyclical effects (automatic stabilisers).

In outright terms, a fiscal deficit that is equivalent to 5 per cent of GDP is more expansionary than a fiscal deficit outcome that is equivalent to 3 per cent of GDP.

To understand the different between policy intent and outcome, we have to explore the issue of decomposing the observed fiscal balance into the discretionary (now called structural) and cyclical components. The latter component is driven by the automatic stabilisers that are in-built into the fiscal process.

The federal (or national) government fiscal balance is the difference between total federal revenue and total federal outlays. So if total revenue is greater than outlays, the fiscal outcome is in surplus and vice versa. It is a simple matter of accounting with no theory involved. However, the fiscal balance is used by all and sundry to indicate the fiscal stance of the government.

So if the fiscal outcome is in surplus it is often concluded that the fiscal impact of government is contractionary (withdrawing net spending) and if the fiscal outcome is in deficit we say the fiscal impact expansionary (adding net spending).

Further, a rising deficit (falling surplus) is often considered to be reflecting an expansionary policy stance and vice versa. What we know is that a rising deficit may, in fact, indicate a contractionary fiscal stance – which, in turn, creates such income losses that the automatic stabilisers start driving the fiscal outcome back towards (or into) deficit.

So the complication is that we cannot conclude that changes in the fiscal impact reflect discretionary policy changes. The reason for this uncertainty clearly relates to the operation of the automatic stabilisers.

To see this, the most simple model of the fiscal balance we might think of can be written as:

Fiscal Balance = Revenue – Spending.

Fiscal Balance = (Tax Revenue + Other Revenue) – (Welfare Payments + Other Spending)

We know that Tax Revenue and Welfare Payments move inversely with respect to each other, with the latter rising when GDP growth falls and the former rises with GDP growth. These components of the fiscal balance are the so-called automatic stabilisers.

In other words, without any discretionary policy changes, the fiscal balance will vary over the course of the business cycle. When the economy is weak – tax revenue falls and welfare payments rise and so the fiscal balance moves towards deficit (or an increasing deficit). When the economy is stronger – tax revenue rises and welfare payments fall and the fiscal balance becomes increasingly positive. Automatic stabilisers attenuate the amplitude in the business cycle by expanding the fiscal outcome in a recession and contracting it in a boom.

So just because the fiscal outcome goes into deficit or the deficit increases as a proportion of GDP doesn’t allow us to conclude that the Government has suddenly become of an expansionary mind. In other words, the presence of automatic stabilisers make it hard to discern whether the fiscal policy stance (chosen by the government) is contractionary or expansionary at any particular point in time.

To overcome this uncertainty, economists devised what used to be called the ‘Full Employment’ or ‘High Employment Budget’. In more recent times, this concept is now called the Structural Balance. The ‘Full Employment Budget Balance’ was a hypothetical construct of the fiscal balance that would be realised if the economy was operating at potential or full employment. In other words, calibrating the fiscal position (and the underlying fiscal parameters) against some fixed point (full capacity) eliminated the cyclical component – the swings in activity around full employment.

So a ‘Full Employment Budget’ would be balanced if total outlays and total revenue were equal when the economy was operating at total capacity. If the fiscal outcome was in surplus at full capacity, then we would conclude that the discretionary structure of the fiscal outcome was contractionary and vice versa if the fiscal outcome was in deficit at full capacity.

The calculation of the structural deficit spawned a bit of an industry in the past with lots of complex issues relating to adjustments for inflation, terms of trade effects, changes in interest rates and more.

Much of the debate centred on how to compute the unobserved full employment point in the economy. There were a plethora of methods used in the period of true full employment in the 1960s. All of them had issues but like all empirical work – it was a dirty science – relying on assumptions and simplifications. But that is the nature of the applied economist’s life.

As I explain in the blog posts cited below, the measurement issues have a long history and current techniques and frameworks based on the concept of the Non-
Accelerating Inflation Rate of Unemployment (the NAIRU) bias the resulting analysis such that actual discretionary positions which are contractionary are seen as being less so and expansionary positions are seen as being more expansionary.

The result is that modern depictions of the structural deficit systematically understate the degree of discretionary contraction coming from fiscal policy.

So the data provided by the question could indicate a more expansionary fiscal intent from government but it could also indicate a large automatic stabiliser (cyclical) component.

But it remains that the statement is True without knowing the breakdown of the actual fiscal position.

You might like to read these blog posts for further information:

• Structural deficits and automatic stabilisers
• Structural deficits – the great con job!

Question 2:

If the external balance remains in surplus and is adding to total spending, then the national government can run a fiscal surplus without impeding economic growth.

The answer is True.

The question asks whether the can run a fiscal surplus without impeding growth rather than whether it always can.

To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

(1) GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.

We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all tax revenue minus total transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).

Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).

Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):

(2) GNP = C + I + G + (X – M) + FNI

To render this approach into the sectoral balances form, we subtract total net taxes (T) from both sides of Expression (3) to get:

(3) GNP – T = C + I + G + (X – M) + FNI – T

Now we can collect the terms by arranging them according to the three sectoral balances:

(4) (GNP – C – T) – I = (G – T) + (X – M + FNI)

The the terms in Expression (4) are relatively easy to understand now.

The term (GNP – C – T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.

The left-hand side of Equation (4), (GNP – C – T) – I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP – C – T).

In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.

The term (G – T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.

Finally, the other right-hand side term (X – M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.

In English we could say that:

The private financial balance equals the sum of the government financial balance plus the current account balance.

We can re-write Expression (6) in this way to get the sectoral balances equation:

(5) (S – I) = (G – T) + CAB

which is interpreted as meaning that government sector deficits (G – T > 0) and current account surpluses (CAB > 0) generate national income and net financial assets for the private domestic sector.

Conversely, government surpluses (G – T < 0) and current account deficits (CAB < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets.

Expression (5) can also be written as:

(6) [(S – I) – CAB] = (G – T)

where the term on the left-hand side [(S – I) – CAB] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance.

This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit).

The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers.

All these relationships (equations) hold as a matter of accounting and not matters of opinion.

If the external balance remains in surplus and is adding to total spending, then the national government can run a fiscal surplus without impeding economic growth.

Thus, when an external deficit (X – M < 0) and public surplus (G – T < 0) coincide, there must be a private domestic deficit. While private spending can persist for a time under these conditions using the net savings of the external sector, the private sector becomes increasingly indebted in the process.

Second, you then have to appreciate the relative sizes of these balances to answer the question correctly.

Consider the following Table which depicts three cases – two that define a state of macroeconomic equilibrium (where aggregate demand equals income and firms have no incentive to change output) and one (Case 2) where the economy is in a disequilibrium state and income changes would occur.

Note that in the equilibrium cases, the (S – I) = (G – T) + (X – M) whereas in the disequilibrium case (S – I) > (G – T) + (X – M) meaning that aggregate demand is falling and a spending gap is opening up. Firms respond to that gap by decreasing output and income and this brings about an adjustment in the balances until they are back in equality.

So in Case 1, assume that the private domestic sector desires to save 2 per cent of GDP overall (spend less than they earn) and the external sector is running a surplus equal to 4 per cent of GDP.

In that case, aggregate demand will be unchanged if the government runs a surplus of 2 per cent of GDP (noting a negative sign on the government balance means T > G).

In this situation, the surplus does not undermine economic growth because the injections into the spending stream (NX) are exactly offset by the leakages in the form of the private saving and the fiscal surplus. This is the Norwegian situation.

In Case 2, we hypothesise that the private domestic sector now wants to save 6 per cent of GDP and they translate this intention into action by cutting back consumption (and perhaps investment) spending.

Clearly, aggregate demand now falls by 4 per cent of GDP and if the government tried to maintain that surplus of 2 per cent of GDP, the spending gap would start driving GDP downwards.

The falling income would not only reduce the capacity of the private sector to save but would also push the fiscal balance towards deficit via the automatic stabilisers. It would also push the external surplus up as imports fell. Eventually the income adjustments would restore the balances but with lower GDP overall.

So Case 2 is a not a position of rest – or steady growth. It is one where the government sector (for a given net exports position) is undermining the changing intentions of the private sector to increase their overall saving.

In Case 3, you see the result of the government sector accommodating that rising desire to save by the private sector by running a deficit of 2 per cent of GDP.

So the injections into the spending stream are 4 per cent from NX and 2 per cent from the deficit which exactly offset the desire of the private sector to save 6 per cent of GDP. At that point, the system would be in rest.

This is a highly stylised example and you could tell a myriad of stories that would be different in description but none that could alter the basic point.

If the drain on spending outweighs the injections into the spending stream then GDP falls (or growth is reduced).

So even though an external surplus is being run, the desired fiscal balance still depends on the saving desires of the private domestic sector. Under some situations, these desires could require a deficit even with an external surplus.

You may wish to read the following blog posts for more information:

• Back to basics – aggregate demand drives output
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!
• Barnaby, better to walk before we run
• Saturday Quiz – June 19, 2010 – answers and discussion

Question 3

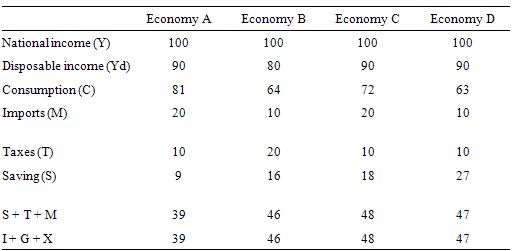
Consider the following table which describes four different economies in terms of the behavioural parameters relating to the leakages to aggregate demand.

Assume that in all four economies, there is idle capacity, the central bank holds all interest rates constant, inflation is constant and there are no changes in international competitiveness.

Which economy would deliver the largest national income bonus for a given discretionary expansion in government spending.

The answer is Economy A.

This question requires you to understand the impact of the different leakages (drains) to aggregate demand that arise from household saving, government taxation and import expenditure.

These leakages combine to determine the spending multiplier.

Students begin to learn about the expenditure multiplier in a very simple model without government or external sector. It sets them up immediately to disregard the crucial relationship between government and non-government sector that really drives the dynamics of the monetary system.

In our macroeconomics text book the government/non-government relationship is introduced at the beginning of the learning process to ensure students understand the importance of net positions and the central role of the government (as the currency-issuer) in the monetary system.

So I don’t think it is too hard to explain the expenditure multiplier with government spending, taxes and imports introduced from the start.

The clue is to first of all realise that aggregate demand drives output with generates incomes (via payments to the productive inputs). I won’t go into controversies here about whether the productive inputs are rewarded fairly or whether surplus value is expropriated etc. That is a separate and not unimportant discussion but not germane here to understand the accounting and the dynamics.

Accordingly, what is spent will generate income in that period which is available for use. The uses are further consumption; paying taxes and/or buying imports. We consider imports as a separate category (even though they reflect consumption, investment and government spending decisions) because they constitute spending which does not recycle back into the production process. They are thus considered to be “leakages” from the expenditure system.

So if for every dollar produced and paid out as income, if the economy imports around 20 cents in the dollar, then only 80 cents is available within the system for spending in subsequent periods excluding taxation considerations.

However there are two other “leakages” which arise from domestic sources – saving and taxation. Take taxation first. When income is produced, the households end up with less than they are paid out in gross terms because the government levies a tax. So the income concept available for subsequent spending is called disposable income (Yd).

To keep it simple, imagine a proportional tax of 20 cents in the dollar is levied, so if $100 of income is generated, $20 goes to taxation and Yd is $80 (what is left). So taxation (T) is a “leakage” from the expenditure system in the same way as imports are.

Finally consider saving. Consumers make decisions to spend a proportion of their disposable income. The amount of each dollar they spent at the margin (that is, how much of every extra dollar to they consume) is called the marginal propensity to consume. If that is 0.80 then they spent 80 cents in every dollar of disposable income.

So if total disposable income is $80 (after taxation of 20 cents in the dollar is collected) then consumption (C) will be 0.80 times $80 which is $64 and saving will be the residual – $26. Saving (S) is also a “leakage” from the expenditure system.

It is easy to see that for every $100 produced, the income that is generated and distributed results in $64 in consumption and $36 in leakages which do not cycle back into spending.

For income to remain at $100 in the next period the $36 has to be made up by what economists call “injections” which in these sorts of models comprise the sum of investment (I), government spending (G) and exports (X). The injections are seen as coming from “outside” the output-income generating process (they are called exogenous or autonomous expenditure variables).

Investment is dependent on expectations of future revenue and costs of borrowing. Government spending is clearly a reflection of policy choices available to government. Exports are determined by world incomes and real exchange rates etc.

For GDP to be stable injections have to equal leakages (this can be converted into growth terms to the same effect). The national accounting statements that we have discussed previous such that the government deficit (surplus) equals $-for-$ the non-government surplus (deficit) and those that decompose the non-government sector in the external and private domestic sectors is derived from these relationships.

So imagine there is a certain level of income being produced – its value is immaterial. Imagine that the central bank sees no inflation risk and so interest rates are stable as are exchange rates and domestic wage levels (these simplifications are to to eliminate unnecessary complexity).

The question then is: what would happen if government increased spending by, say, $100? This is the terrain of the multiplier. If aggregate demand increases drive higher output and income increases then the question is by how much?

The spending multiplier is defined as the change in real income that results from a dollar change in exogenous aggregate demand (so one of G, I or X). We could complicate this by having autonomous consumption as well but the principle is not altered.

The spending multiplier is the extra spending that would occur when an autonomous expenditure source changes. So we ask the question: What would be the change in income if I or G or X changed by $1?

To derive the multiplier we need to write out the aggregate demand model and substitute the behavioural parameters into the model.

Aggregate demand (and income)

Y = C + I + G + X – M

Taxes

T = t*Y.

The little t is the marginal tax rate which in this case is the proportional rate. Note here taxes are taken out of total income (Y) which then defines disposable income.

The * sign denotes multiplication. You can do this example in a spreadsheet if you like.

Yd = (1-t)*Y

Consumption and Saving

We define the consumption relationship at the most simple level as a proportional relationship to disposable income (Yd).

C = c*Yd

where little c is the marginal propensity to consume (MPC) or the fraction of every dollar of disposable income consumed.

So using the Yd relationship we can write consumption as:

C = c*(1-t)*Y

Imports

Imports (M) are considered proportional to total income (Y):

M= m*Y

where little m is the marginal propensity to import which is the increase in imports for every real GDP dollar produced.

Multiplier

To derive the multiplier formula we can assemble the aggregate demand relationship with its individual behavioural components as follows:

Y = C + I + G + X – M

Y = c*(1-t)*Y + I + G + X – m*Y

Now, re-arrange the equation to collect the Y terms on the left-hand side:

Y – c*(1-t)*Y + m*Y = I + G + X

You can see the exogenous injections to aggregate demand (those not reliant on national income) are on the right-hand side and all the components of expenditure that rely on national income are collected on the left-hand side.

We simplify this as follows:

Y(1 – c*(1-t) + m) = I + G + X

So the relationship between changes in Y and changes in the exogenous spending components is:

Y = [1/(1 – c*(1-t) + m)]*(I + G + X)

The term in [ ] brackets on the right-hand side is the multiplier because it shows how much a given change in (I + G + X) multiply to national income Y.

We could write this as:

Y = k*(I + G + X)

where

k = [1/(1 – c*(1-t) + m)]

Or using other symbols:

k = 1/(1 – MPC x (1-t) + MPM)

So the higher is the MPC the lower is the tax rate (t) and the lower is the MPM the higher is the multiplier. That makes sense because taxes and imports drain spending from the income generating system. So as income responds positively to an autonomous injection, the smaller are the drains via taxation and imports and the higher the induced consumption – the higher is the second round spending effect which then continues to generate further income increases.

We can then apply this knowledge to the four economies in the Table. The bottom row of the Table provide the solution to the multiplier for the given parameters.

We interpret the data as follows. If government spending increased by $1, then the total change in national income in Economy A would be $2.56, in Economy B $2.17, in Economy C $2.08, and in Economy D $2.13.

The question obviously requires you to think about the different impacts of varying the drains on aggregate demand. The drains are not all equal.

For example, a given change in the marginal propensity to import has a greater impact than a given change in the marginal propensity to consume as you can see by comparing Economy C to Economy D. This is because imports come out of pre-tax income whereas the consumption decision comes out of disposable income.

A rise in the marginal propensity to consume of 0.1 will more than offset the draining impact of an equal rise in the tax rate because the decline in saving is greater than the rise in taxes.

You can construct all sorts of different scenarios to understand the impacts. To give you an idea of the different compositions of aggregate demand and the different leakages and injections the following Table assumes national income is 100 and then solves the model for each economy given the parameters.

I could clearly make the model more complex but the results would not be very different. Some will suggest the model is overly simplistic because it is a “fixed price” model and assumes supply will just meet any new nominal spending. That is true by construction and is a reasonable description of the state of play at present.

There is no inflation threat at present due to the vast quantities of idle resources that can be brought into production should there be a demand for their services.

Some might argue the external sector is too simplistic and that the terms of trade (real exchange rate) should be included in the export and import relationships. In a complex model that is true but in the context of this model the likely changes would just reinforce the results I derive. There is no loss of insight by holding the terms of trade constant.

Some might argue that the interest rate should be modelled and I reply why? The implicit assumption is that the central bank sets the interest rate and it is currently low in most nations and has been for some years. With no real inflation threat, the short-term rates will remain low for some time yet.

As to long rates (and the rising fiscal deficit) – show me where the significant rises in fiscal deficits (for a sovereign nation) are driving up rates. They have actually been falling as a consequence of very strong demand for public debt issues (almost insatiable) by bond markets and the quantitative easing efforts of the large central banks.

For an EMU nation, long-rates are within the control of the ECB as has been demonstrated once it started buying government bonds in the secondary markets. So leaving monetary policy implicit and fixed in this model doesn’t lose any insight or “fix” the results in my favour.

You may wish to read the following blog posts for more information:

• Spending multipliers
• Saturday Quiz – October 16, 2010 – answers and discussion

That is enough for today!

(c) Copyright 2019 William Mitchell. All Rights Reserved.