Saturday Quiz – July 5, 2014 – answers and discussion

July 6, 2014
bill
Saturday quiz
0 Comments

Here are the answers with discussion for yesterday’s quiz. The information provided should help you understand the reasoning behind the answers. If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

If the inflation rate is steady and the central bank maintains a constant nominal interest rate, then under current institutional arrangements where governments match deficit spending with debt issuance to the private sector, the public debt ratio will rise if the government deficit doubles (say, from 2 to 4 per cent of GDP).

The answer is False.

There are two concepts that are central to the question: (a) a rising fiscal deficit – which is a flow and not scaled by GDP in this case; and (b) a rising public debt ratio which by construction (as a ratio) is scaled by GDP.

The two concepts are not commensurate although they are related in some way.

A rising fiscal deficit does not necessary lead to a rising public debt ratio. You might like to refresh your understanding of these concepts by reading this blog – Saturday Quiz – March 6, 2010 – answers and discussion.

While the mainstream macroeconomics argues that a sovereign government is revenue-constrained and is subject to the ‘government budget constraint’, MMT places no particular importance in the public debt to GDP ratio for a sovereign government, given that insolvency is not an issue.

The mainstream framework for analysing the so-called “financing” choices faced by a government (taxation, debt-issuance, money creation) – the ‘government budget constraint’ – is written as:

Which you can read in English as saying that Budget deficit = Government spending + Government interest payments – Tax receipts must equal (be “financed” by) a change in Bonds (B) and/or a change in high powered money (H). The triangle sign (delta) is just shorthand for the change in a variable.

Remember, this is merely an accounting statement. In a stock-flow consistent macroeconomics, this statement will always hold. That is, it has to be true if all the transactions between the government and non-government sector have been correctly added and subtracted (accounted for).

From the perspective of Modern Monetary Theory (MMT), the previous equation is just an ex post accounting identity that has to be true by definition and has no real economic importance.

For the mainstream economist, the equation represents an ex ante (before the fact) financial constraint that the government is bound by. The difference between these two conceptions is very significant and the second (mainstream) interpretation cannot be correct if governments issue fiat currency (unless they place voluntary constraints on themselves to act as if it is).

That interpretation is inapplicable (and wrong) when applied to a sovereign government that issues its own currency.

But the accounting relationship can be manipulated to provide an expression linking deficits and changes in the public debt ratio.

The following equation expresses the relationships above as proportions of GDP:

The change in the debt ratio is the sum of two terms on the right-hand side: (a) the difference between the real interest rate (r) and the GDP growth rate (g) times the initial debt ratio; and (b) the ratio of the primary deficit (G-T) to GDP. A primary fiscal balance is the difference between government spending (excluding interest rate servicing) and taxation revenue.

The real interest rate is the difference between the nominal interest rate and the inflation rate. If inflation is maintained at a rate equal to the interest rate then the real interest rate is constant.

A growing economy can absorb more debt and keep the debt ratio constant or falling. From the formula above, if the primary fiscal balance is zero, public debt increases at a rate r but the public debt ratio increases at r – g.

For example, if r = 0, and g = 2, the primary deficit ratio could equal 2 per cent (of GDP) and the public debt ratio would be unchanged. Doubling the primary deficit to 4 per cent would require g to rise to 4 for the public debt ratio to remain unchanged. That is entirely possible.

A nation running a primary deficit can obviously reduce its public debt ratio over time or hold it constant if growth is stimulated. Further, you can see that even with a rising primary deficit, if output growth (g) is sufficiently greater than the real interest rate (r) then the debt ratio can fall from its value last period.

Furthermore, depending on contributions from the external sector, a nation running a deficit will more likely create the conditions for a reduction in the public debt ratio than a nation that introduces an austerity plan aimed at running primary surpluses.

Clearly, the real growth rate has limits and that would limit the ability of a government (that voluntarily issues debt) to hold the debt ratio constant while expanding its fiscal deficit as a proportion of GDP.

The following blog may be of further interest to you:

Saturday Quiz – March 6, 2010 – answers and discussion

Question 2:

The real material living standards of workers are systematically eroded when the wage share in national income declines in favour of a higher profit share.

The answer is False.

The wage share is related to workers’ real living standards but does not define them.

The wage share in nominal GDP is expressed as the total wage bill as a percentage of nominal GDP. Economists differentiate between nominal GDP ($GDP), which is total output produced at market prices and real GDP (GDP), which is the actual physical equivalent of the nominal GDP. We will come back to that distinction soon.

To compute the wage share we need to consider total labour costs in production and the flow of production ($GDP) each period.

Employment (L) is a stock and is measured in persons (averaged over some period like a month or a quarter or a year.

The wage bill is a flow and is the product of total employment (L) and the average wage (w) prevailing at any point in time. Stocks (L) become flows if it is multiplied by a flow variable (W). So the wage bill is the total labour costs in production per period.

So the wage bill = W.L

The wage share is just the total labour costs expressed as a proportion of $GDP – (W.L)/$GDP in nominal terms, usually expressed as a percentage. We can actually break this down further.

Labour productivity (LP) is the units of real GDP per person employed per period. Using the symbols already defined this can be written as:

LP = GDP/L

so it tells us what real output (GDP) each labour unit that is added to production produces on average.

We can also define another term that is regularly used in the media – the real wage – which is the purchasing power equivalent on the nominal wage that workers get paid each period. To compute the real wage we need to consider two variables: (a) the nominal wage (W) and the aggregate price level (P).

We might consider the aggregate price level to be measured by the consumer price index (CPI) although there are huge debates about that. But in a sense, this macroeconomic price level doesn’t exist but represents some abstract measure of the general movement in all prices in the economy.

The real wage (w) tells us what volume of real goods and services the nominal wage (W) will be able to command and is obviously influenced by the level of W and the price level. For a given W, the lower is P the greater the purchasing power of the nominal wage and so the higher is the real wage (w).

We write the real wage (w) as W/P. So if W = 10 and P = 1, then the real wage (w) = 10 meaning that the current wage will buy 10 units of real output. If P rose to 2 then w = 5, meaning the real wage was now cut by one-half.

So the proposition in the question – that a declining wage share means the real standard of living for workers is falling – is false.

Irrespective of what happens to the wage share, as long as the real wage is rising, material standards of living will be rising (other things equal). That is, a declining wage share per se doesn’t denote a decline in workers’ living standards.

What it tells us is that a rising proportion of national income is going to profits (non-wages). But that rising proportion could be in relation to an overall expanding pie.

A declining wage share is consistent with growth in the real wage which is slower than the growth in labour productivity. If the real wage is growing but labour productivity is growing faster, then the wage share will fall.

A declining wage share driven by a real wage falling (and labour productivity at least not falling by as much) would signify a decline in living standards but that is because the real wage is falling.

The following blogs may be of further interest to you:

Question 3:

Suppose that the government announced as part of a fiscal austerity strategy that it intended to cut its deficit from 4 per cent of GDP to 2 per cent in the coming year and during that year net exports were projected to move from a deficit of 1 per cent of GDP to a surplus of 1 per cent of GDP. In that situation we would not be able to conclude that the fiscal austerity plans would undermine growth if the net export projection was realised.

The answer is True.

This question requires an understanding of the sectoral balances that can be derived from the National Accounts. But it also requires some understanding of the behavioural relationships within and between these sectors which generate the outcomes that are captured in the National Accounts and summarised by the sectoral balances.

From an accounting sense, if the external sector goes into surplus (positive net exports) there is scope for the government balance to move into surplus without compromising growth as long as the external position more than offsets any actual private domestic sector net saving.

Skip the next section explaining the balances if you are familiar with the derivation. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced.

Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

From the uses perspective, national income (GDP) can be used for:

GDP = C + S + T

which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.

Equating these two perspectives we get:

C + S + T = GDP = C + I + G + (X – M)

So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.

(I – S) + (G – T) + (X – M) = 0

That is the three balances have to sum to zero. The sectoral balances derived are:

The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
The Budget Deficit (G – T) – negative if in surplus, positive if in deficit.
The Current Account balance (X – M) – positive if in surplus, negative if in deficit.

These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.

A simplification is to add (I – S) + (X – M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).

This is also a basic rule derived from the national accounts and has to apply at all times.

If the nation is running an external surplus it means that the contribution to aggregate demand from the external sector is positive – that is net spending injection – providing a boost to domestic production and income generation.

The extent to which this allows the government to reduce its deficit (by the same amount as the move into external surplus) and not endanger growth depends on the private domestic sector’s spending decisions (overall). If the private domestic sector runs a deficit, then the fiscal austerity strategy will work under the assumed conditions – inasmuch as the goal is to reduce the fiscal deficit without compromising growth.

But this strategy would be unsustainable as it would require the private domestic sector overall to continually increase its indebtedness.

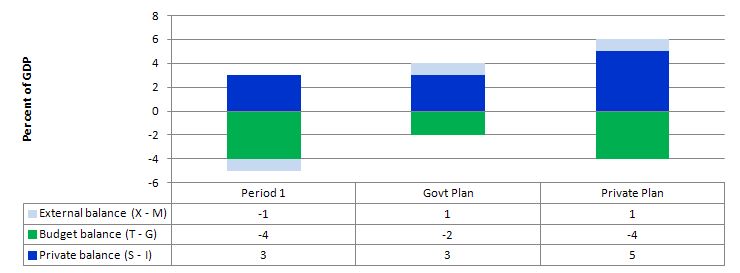
The following graph captures what might happen if the private domestic sector (households and firms) seeks to increase its overall saving at the same time the net exports are rising and the government deficit is falling.

In Period 1, there is an external deficit of 1 per cent of GDP and a fiscal deficit of 4 per cent of GDP which generates income sufficient to allow the private domestic sector to run a surplus (S – I > 0) of 3 per cent of GDP.

The Government plans to cut its deficit to 2 per cent of GDP by cutting spending. To achieve that with net exports rising to 1 per cent of GDP and for there to be no change in aggregate demand then the private domestic sector is assumed not to be changing its saving behaviour.

However, what happens if the private sector, fearing the contractionary forces coming from the announced cuts in public spending and not really being in a position to assess what might happen to net exports over the coming period, decides to increase its saving. In other words, they plan to increase net saving to 5 per cent of GDP – the situation captured under the Private Plan option.

In this case, if the private sector actually succeeded in reducing its spending and increasing its saving balance to 5 per cent of GDP, the national income shifts would ensure the government could not realise its planned deficit reduction.

The public and private plans are clearly not compatible and the resolution of their competing objectives would be achieved by national income shifts.

In other words, as the private sector and the public sector reduced their spending in pursuit of their plans, income would contract even though net exports were rising.

So unless private sector behaviour remains constant the government cannot rely on an increase in net exports to provide the space for them to cut their own net spending.

Thus, in general, with the government contracting the only way the private domestic sector could successfully increase its net saving is if the injection from the external sector offsett the drain from the domestic sector (public and private). Otherwise, income will decline and both the government and private domestic sector will find it difficult to reduce their net spending positions.

Take a balanced fiscal position, then income will decline unless the private domestic sector’s saving overall is just equal to the external surplus. If the private domestic sector tried to push its position further into surplus then the following story might unfold.

Consistent with this aspiration, households may cut back on consumption spending and save more out of disposable income. The immediate impact is that aggregate demand will fall and inventories will start to increase beyond the desired level of the firms.

The firms will soon react to the increased inventory holding costs and will start to cut back production. How quickly this happens depends on a number of factors including the pace and magnitude of the initial demand contraction. But if the households persist in trying to save more and consumption continues to lag, then soon enough the economy starts to contract – output, employment and income all fall.

The initial contraction in consumption multiplies through the expenditure system as workers who are laid off also lose income and their spending declines. This leads to further contractions.

The declining income leads to a number of consequences. Net exports improve as imports fall (less income) but the question clearly assumes that the external sector remains in deficit. Total saving actually starts to decline as income falls as does induced consumption.

So the initial discretionary decline in consumption is supplemented by the induced consumption falls driven by the multiplier process.

The decline in income then stifles firms’ investment plans – they become pessimistic of the chances of realising the output derived from augmented capacity and so aggregate demand plunges further. Both these effects push the private domestic balance further towards and eventually into surplus

With the economy in decline, tax revenue falls and welfare payments rise which push the public fiscal balance towards and eventually into deficit via the automatic stabilisers.

If the private sector persists in trying to increase its saving ratio then the contracting income will clearly push the fiscal balance into deficit.

So the external position has to be sufficiently strong enough to offset the domestic drains on expenditure. The answer is thus not clear.

The following blogs may be of further interest to you: