Growth and Inequality – Part 1

I am now using Friday’s blog space to provide draft versions of the Modern Monetary Theory textbook that I am writing with my colleague and friend Randy Wray. We expect to publish the text sometime around mid-2014. Our (very incomplete) textbook homepage – Modern Monetary Theory and Practice – has draft chapters and contents etc in varying states of completion. Comments are always welcome. Note also that the text I post here is not intended to be a blog-style narrative but constitutes the drafting work I am doing – that is, the material posted will not represent the complete text. Further it will change as the drafting process evolves.

Chapter X Growth and Inequality

X.1 Overview

Throughout this textbook we have been examining what determines fluctuations in the trade cycle. This has typically been referred to as short-run analysis, because it assumes that the stock of productive capital available (machinery, equipments, skills and experience, etc) are fixed over the period the analysis is being conducted.

We have also noted that contemporary issues relating to the ageing society and reducing poverty rates in nations requires a consideration of what economists term the long-run. In this regard, we focus on what determines productivity and productivity growth.

Productivity growth, which allows real income to grow, is the single most important determinant of our material standard of living and the trading standings between nations.

When we considered the determinant of aggregate supply and employment we were content to define productivity as output per unit of input.

We thus calculated labour productivity as the total value of real output divided by total employment or total hours worked. So if a firm produced 1000 units of output each day and employed 100 workers in the process, then the labour productivity of that plant would be 10.

There are many conceptual issues involved in measuring labour productivity. For example, it is rarely the case that we can isolate productive inputs. Further, how do we account for different labour skills that are deployed to produce a given volume of output?

Economists also compute measures of total factor productivity which attempts to include the contributions to final output of all the inputs used – capital, labour, organisation, etc.

Figure X.1 shows real output per hour worked index for the US nonfarm business sector (2009=100). The grey bars are the US recession periods as specified by the National Bureau of Economic Research.

There are two points to note. First, productivity is a cyclical variable, tending to decline during a recession and pick up at the end of the recession. We have discussed this phenomena in Chapter 13.

To refresh your memory, when firms face declining orders, they reduce output at a slower rate than they reduce their workforce. firms tend to hoard certain categories of labour during an downturn in the economic cycle. For example, firms are reluctant to sack skilled labour because it is expensive to recruit and train. Further, maintenance of operations requires a certain complement of overhead labour, for example, front-desk staff, telephonists etc.

Firms also will turn machines off or run their capital at slower speeds as they adjust their output volumes down to meet the declining sales volume.

Thus productivity declines during a downturn because less output is being produced for a given quantity of inputs.

In the recovery, as sales pick up, output rises and the hoarded labour works more intensively and machinery is brought back into higher rates of utilisation. As a result productivity rises.

Second, productivity grows over time at various rates. We call this the long-run or secular trend in productivity.

For the US, the 1980s were a period of slower productivity growth relative to earlier and later periods. In this chapter we will consider what determines long-run productivity growth.

Figure X.1 Nonfarm Business Sector: Real Output Per Hour of All Persons, US, 1940-2013, 2009=100

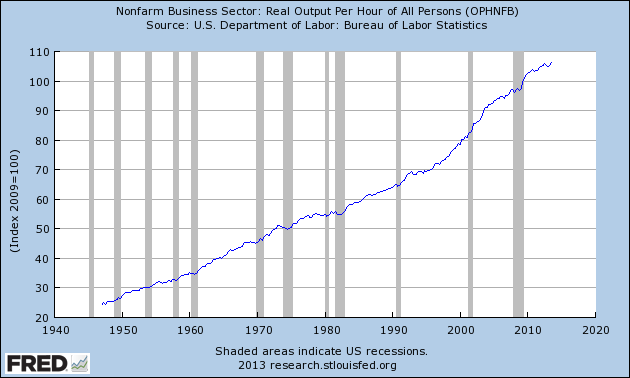
Source: U.S. Department of Labor: Bureau of Labor Statistics, Productivity and Costs.

The US Bureau of Labor Statistics (BLS) provides an excellent source of data that permits international labour comparisons – http://www.bls.gov/fls/

Figure X.2 compares the evolution of output per employed person in manufacturing for selected nations from 1950 to 2011 (1875 = 100).

The common base year allows us to compare relative growth rates in productivity across nations. In the period since 1975, Japan was the leading nation as its pace of industrialisation expanded but by 1999, the US had overtaken Japan, which still remained ahead of the other nations shown.

Australia and Germany have been relatively low productivity nations with the UK and France tracking each other closely.

Once again you can see the marked cyclical behaviour of productivity during global financial crisis (2009) where productivity fell sharply in most nations.

Figure X.2 Output per employed person in manufacturing in selected nations, 1950-2013, 1975=100

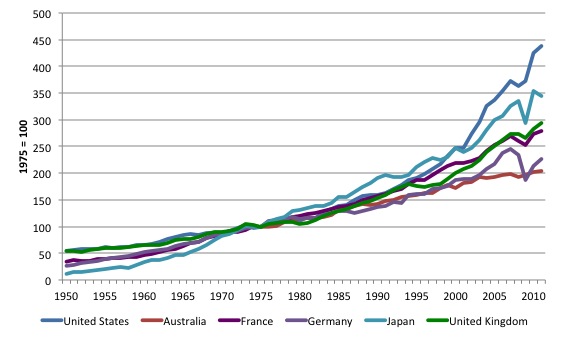
Source: U.S. Department of Labor: Bureau of Labor Statistics, International Labor Statistics.

Table X.1 shows annual percentage growth in Output per employed person in manufacturing in selected nations from 1950-51 to 2010-11.

The data provides a rich source of information on the shifting world patterns in manufacturing over time. For example, in the immediate Post World War II period, the reconstruction of Japan meant it achieved outstanding productivity growth relative to the other nations. The war-torn European nations (Germany, Italy, Netherlands) also enjoyed strong productivity growth.

More recently, the newly industrialising nations such as Korea and Singapore have enjoyed strong growth as the more mature industrial nations have witnessed slowing productivity growth.

To help you understand the implications of the productivity growth variations consider Australia, which in the decade to 2000 grew on average at 2 per cent per annum but slowed to 1.5 per cent per annum in the decade 2000-10.

Using compounding formula (the well-known Rule of 72 – see box), we know that if productivity growth is 2 per cent, then real income will double every 36 years.

If productivity growth drops to 1.5 per cent, then real income will double every 48 years. In the case of the US, where productivity growth was averaging 5.4 per cent per annum between 2000-10, real income will double each 13 odd years. Of-course, before we can conclude what this means for the average citizen we also would need to know about the distribution of income. The US has rising income inquality and is overall less equal than Australia, so the advances in material standards of living provided for by productivity growth are less evenly shared in the US than, say, in Australia.

Table X.1 Output per employed person in manufacturing in selected nations, 1950-2013, 1975=100

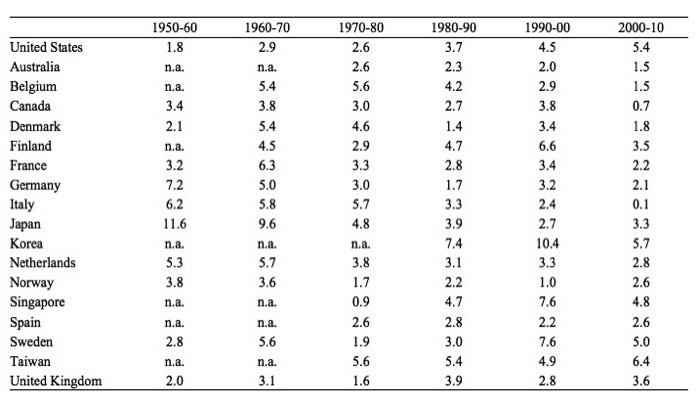
Source: U.S. Department of Labor: Bureau of Labor Statistics, International Labor Statistics.

X.2 Keynesian growth theories – Harrod-Domar

An early growth theory came from Roy Harrod in 1939 when he attempted to provide a long-run reconstruction of Keynes’ General Theory. Eight years later, Evsey Domar introduced a model of long-run growth, which added to the approach taken by Harrod. It is conventional to refer to this work as the Harrod-Domar growth model.

There are three components to their model:

1. The warranted rate of growth, which is the rate of growth that maintains full utilisation of capital.

2. The natural rate of growth, which is the rate of growth that ensures that all workers that desire work can find employment. Equilibrium occurs when the warranted rate of growth equals the natural rate of growth.

3. The razor’s edge or instability of growth, where the two rates of growth which define a full employment equilibrium are prone to deviate and cause crisis.

To see the derivation of the Harrod-Domar model we assume a very simple model of income determination:

(X.1)      Y_t = C_t + I_t

where Y_t is total output/income in period t, C_t is total consumption in period t, and I_t is total investment in period t.

We are assuming a closed economy for simplicity.

Income can be either consumed or saved and S_t = sY_t, where s is the marginal propensity to save (which is 1 – the marginal propensity to consume).

Thus:

(X.2)      Y_t = C_t + I_t = C_t + S_t

In equilibrium:

(X.3)      S_t = I_t

Capital is accumulated over time according to the following expression:

(X.4)      K_t+1 = I_t + K_t(1 – δ)

where K is the capital stock, and δ is the rate of depreciation of the existing capital stock (K_t). In other words, the capital stock increases as a result of the flow of investment in the current period taking into account the depreciation of existing capital.

From, Equation (X.3), we can re-write the capital accumulation relationship as:

(X.5)      K_t+1 = sY_t + K_t(1 – δ)

If we assume there is no depreciation (δ = 0) then (X.5) simplifies to:

(X.6)      K_t+1 = sY_t + K_t

Noting that ΘK_t+1 – ΘK_t = ΔK, then:

(X.7)      ΔK_t = sY_t

Warranted rate of growth

The warranted rate of growth ensures that all available capital is fully employed.

We define a fixed output-capital ratio which is an indicator of the productivity of capital:

(X.8)      Θ = Y_t/K_t

The magnitude of Θ determines how much capital is required per unit of output. High values of Θ means that a nation will require large capital stocks to produce and vice versa. For now, we will abstract from issues such as quality of capital and how we might value the heterogenous items (machines, equipment etc) that are aggregated in a single measure of a nation’s capital stock.

Note that:

(X.8)      Y_t = ΘK_t

If Θ is fixed, then Equation (X.7) means that to increase output, more capital has to be added in proportions dictated by Θ

Thus:

(X.9)      ΔY_t = ΘΔK_t

If we substitute Equation (X.7) into (X.9) we get:

(X.10)      ΔY_t = ΘsY_t

If we divide both sides by Y_t, Equation (X.10) becomes a growth relationship:

(X.11)      g = Θs

We drop the subscripts to simplify and note that g is the warranted rate of growth in output, which given the fixed output-capital ratio will ensure the current capital stock is fully utilised.

Natural rate of growth

NEXT WEEK AND ANALYSIS OF INSTABILITY

References

Domar, E. (1947) ‘Expansion and Employment’, American Economic Review, 37, 34-55.

Harrod, R. (1939) ‘An Essay in Dynamic Theory’, Economic Journal, 49, 14-33.

Conclusion

CONTINUING NEXT FRIDAY.

Saturday Quiz

The Saturday Quiz will be back again tomorrow. It will be of an appropriate order of difficulty (-:

That is enough for today!

(c) Copyright 2013 Bill Mitchell. All Rights Reserved.