Saturday Quiz – March 30, 2013 – answers and discussion

Here are the answers with discussion for yesterday’s quiz. The information provided should help you work out why you missed a question or three! If you haven’t already done the Quiz from yesterday then have a go at it before you read the answers. I hope this helps you develop an understanding of Modern Monetary Theory (MMT) and its application to macroeconomic thinking. Comments as usual welcome, especially if I have made an error.

Question 1:

The larger the balances that the commercial banks have on account with the central bank the more they can lend to customers.

The answer is False.

This is a question about whether you understand the flawed concept of the money multiplier and bank reserves.

Mainstream macroeconomics textbooks present a flawed depiction of the credit-creation capacity of commercial banks. The concept of the money multiplier is at the centre of this analysis and posits that the multiplier m transmits changes in the so-called monetary base (MB) (the sum of bank reserves and currency at issue) into changes in the money supply (M). The chapters on money usually present some arcane algebra which is deliberately designed to impart a sense of gravitas or authority to the students who then mindlessly ape what is in the textbook.

They rehearse several times in their undergraduate courses (introductory and intermediate macroeconomics; money and banking; monetary economics etc) the mantra that the money multiplier is usually expressed as the inverse of the required reserve ratio plus some other novelties relating to preferences for cash versus deposits by the public.

Accordingly, the students learn that if the central bank told private banks that they had to keep 10 per cent of total deposits as reserves then the required reserve ratio (RRR) would be 0.10 and m would equal 1/0.10 = 10. More complicated formulae are derived when you consider that people also will want to hold some of their deposits as cash. But these complications do not add anything to the story.

The formula for the determination of the money supply is: M = m x MB. So if a $1 is newly deposited in a bank, the money supply will rise (be multiplied) by $10 (if the RRR = 0.10). The way this multiplier is alleged to work is explained as follows (assuming the bank is required to hold 10 per cent of all deposits as reserves):

• A person deposits say $100 in a bank.
• To make money, the bank then loans the remaining $90 to a customer.
• They spend the money and the recipient of the funds deposits it with their bank.
• That bank then lends 0.9 times $90 = $81 (keeping 0.10 in reserve as required).
• And so on until the loans become so small that they dissolve to zero

None of this is accurate in terms of depicting how the banks make loans. It is an important device for the mainstream because it implies that banks take deposits to get funds which they can then on-lend. But prudential regulations require they keep a little in reserve. So we get this credit creation process ballooning out due to the fractional reserve requirements.

The money multiplier myth also leads students to think that as the central bank can control the monetary base then it can control the money supply. Further, given that inflation is allegedly the result of the money supply growing too fast then the blame is sheeted hometo the “government”. This leads to claims that if the government runs a budget deficit then it has to issue bonds to avoid causing hyperinflation. Nothing could be further from the truth.

That is nothing like the way the banking system operates in the real world. The idea that the monetary base (the sum of bank reserves and currency) leads to a change in the money supply via some multiple is not a valid representation of the way the monetary system operates.

First, the central bank does not have the capacity to control the money supply in a modern monetary system. In the world we live in, bank loans create deposits and are made without reference to the reserve positions of the banks. The bank then ensures its reserve positions are legally compliant as a separate process knowing that it can always get the reserves from the central bank. The only way that the central bank can influence credit creation in this setting is via the price of the reserves it provides on demand to the commercial banks.

Second, this suggests that the decisions by banks to lend may be influenced by the price of reserves rather than whether they have sufficient reserves. They can always get the reserves that are required at any point in time at a price, which may be prohibitive.

Third, the money multiplier story has the central bank manipulating the money supply via open market operations. So they would argue that the central bank might buy bonds to the public to increase the money base and then allow the fractional reserve system to expand the money supply. But a moment’s thought will lead you to conclude this would be futile unless (as in Question 3 a support rate on excess reserves equal to the current policy rate was being paid).

Why? The open market purchase would increase bank reserves and the commercial banks, in lieu of any market return on the overnight funds, would try to place them in the interbank market. Of-course, any transactions at this level (they are horizontal) net to zero so all that happens is that the excess reserve position of the system is shuffled between banks. But in the process the interbank return would start to fall and if the process was left to resolve, the overnight rate would fall to zero and the central bank would lose control of its monetary policy position (unless it was targetting a zero interest rate).

In lieu of a support rate equal to the target rate, the central bank would have to sell bonds to drain the excess reserves. The same futility would occur if the central bank attempted to reduce the money supply by instigating an open market sale of bonds.

In all cases, the central bank cannot influence the money supply in this way.

Fourth, given that the central bank adds reserves on demand to maintain financial stability and this process is driven by changes in the money supply as banks make loans which create deposits. Banks do not initially need reserves to lend. Reserves are used to facilitate the integrity of the clearing house (payments system). The links below provide more in-depth analysis of that point.

So the operational reality is that the dynamics of the monetary base (MB) are driven by the changes in the money supply which is exactly the reverse of the causality presented by the monetary multiplier.

So in fact we might write MB = M/m, where m is a divisor.

You might like to read these blogs for further information:

• Teaching macroeconomics students the facts
• Lost in a macroeconomics textbook again
• Lending is capital- not reserve-constrained
• Oh no … Bernanke is loose and those greenbacks are everywhere
• Building bank reserves will not expand credit
• Building bank reserves is not inflationary
• 100-percent reserve banking and state banks
• Money multiplier and other myths

Question 2:

The inflation risk of government deficit spending is invariant between matching the change in net spending with funds provided by the central bank or issuing debt to the private bond markets.

The answer is True.

The mainstream macroeconomic textbooks all have a chapter on fiscal policy (and it is often written in the context of the so-called IS-LM model but not always).

The chapters always introduces the so-called Government Budget Constraint (as explained above) that alleges that governments have to “finance” all spending either through taxation; debt-issuance; or money creation. The writer fails to understand that government spending is performed in the same way irrespective of the accompanying monetary operations.

They claim that money creation (borrowing from central bank) is inflationary while the latter (private bond sales) is less so. These conclusions are based on their erroneous claim that “money creation” adds more to aggregate demand than bond sales, because the latter forces up interest rates which crowd out some private spending.

All these claims are without foundation in a fiat monetary system and an understanding of the banking operations that occur when governments spend and issue debt helps to show why.

So what would happen if a sovereign, currency-issuing government (with a flexible exchange rate) ran a budget deficit without issuing debt?
Like all government spending, the Treasury would credit the reserve accounts held by the commercial bank at the central bank. The commercial bank in question would be where the target of the spending had an account. So the commercial bank’s assets rise and its liabilities also increase because a deposit would be made.

The transactions are clear: The commercial bank’s assets rise and its liabilities also increase because a new deposit has been made. Further, the target of the fiscal initiative enjoys increased assets (bank deposit) and net worth (a liability/equity entry on their balance sheet).

Taxation does the opposite and so a deficit (spending greater than taxation) means that reserves increase and private net worth increases.

This means that there are likely to be excess reserves in the “cash system” which then raises issues for the central bank about its liquidity management. The aim of the central bank is to “hit” a target interest rate and so it has to ensure that competitive forces in the interbank market do not compromise that target.

When there are excess reserves there is downward pressure on the overnight interest rate (as banks scurry to seek interest-earning opportunities), the central bank then has to sell government bonds to the banks to soak the excess up and maintain liquidity at a level consistent with the target. Some central banks offer a return on overnight reserves which reduces the need to sell debt as a liquidity management operation.

There is no sense that these debt sales have anything to do with “financing” government net spending. The sales are a monetary operation aimed at interest-rate maintenance. So M1 (deposits in the non-government sector) rise as a result of the deficit without a corresponding increase in liabilities. It is this result that leads to the conclusion that that deficits increase net financial assets in the non-government sector.

What would happen if there were bond sales? All that happens is that the banks reserves are reduced by the bond sales but this does not reduce the deposits created by the net spending. So net worth is not altered. What is changed is the composition of the asset portfolio held in the non-government sector.

The only difference between the Treasury “borrowing from the central bank” and issuing debt to the private sector is that the central bank has to use different operations to pursue its policy interest rate target. If it debt is not issued to match the deficit then it has to either pay interest on excess reserves (which most central banks are doing now anyway) or let the target rate fall to zero (the Japan solution).

There is no difference to the impact of the deficits on net worth in the non-government sector.

Mainstream economists would say that by draining the reserves, the central bank has reduced the ability of banks to lend which then, via the money multiplier, expands the money supply.

However, the reality is that:

• Building bank reserves does not increase the ability of the banks to lend.
• The money multiplier process so loved by the mainstream does not describe the way in which banks make loans.
• Inflation is caused by aggregate demand growing faster than real output capacity. The reserve position of the banks is not functionally related with that process.

So the banks are able to create as much credit as they can find credit-worthy customers to hold irrespective of the operations that accompany government net spending.

This doesn’t lead to the conclusion that deficits do not carry an inflation risk. All components of aggregate demand carry an inflation risk if they become excessive, which can only be defined in terms of the relation between spending and productive capacity.

It is totally fallacious to think that private placement of debt reduces the inflation risk. It does not.

You may wish to read the following blogs for more information:

• Why history matters
• Building bank reserves will not expand credit
• Building bank reserves is not inflationary
• The complacent students sit and listen to some of that
• Saturday Quiz – February 27, 2010 – answers and discussion

Question 3:

Only one of the following propositions is possible (with all balances expressed as a per cent of GDP):

• A nation can run an external deficit and equal government surplus while the private domestic sector is saving overall.
• A nation can run an external deficit and equal government surplus while the private domestic sector is dis-saving overall.
• A nation can run an external deficit and a larger government surplus while the private domestic sector is saving overall.
• None of the above are possible as they all defy the sectoral balances accounting identity.

The best answer is the second option – “A nation can run an external deficit and equal government surplus while the private domestic sector is dis-saving overall”.

This is a question about the sectoral balances – the government budget balance, the external balance and the private domestic balance – that have to always add to zero because they are derived as an accounting identity from the national accounts.

To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.

From the sources perspective we write:

GDP = C + I + G + (X – M)

which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X – M).

From the uses perspective, national income (GDP) can be used for:

GDP = C + S + T

which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.

Equating these two perspectives we get:

C + S + T = GDP = C + I + G + (X – M)

So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.

(I – S) + (G – T) + (X – M) = 0

That is the three balances have to sum to zero. The sectoral balances derived are:

• The private domestic balance (I – S) – positive if in deficit, negative if in surplus.
• The Budget Deficit (G – T) – negative if in surplus, positive if in deficit.
• The Current Account balance (X – M) – positive if in surplus, negative if in deficit.

These balances are usually expressed as a per cent of GDP but that doesn’t alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.

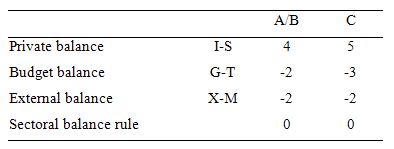
The following Table represents the three options in percent of GDP terms. To aid interpretation remember that (I-S) > 0 means that the private domestic sector is spending more than they are earning; that (G-T) < 0 means that the government is running a surplus because T > G; and (X-M) < 0 means the external position is in deficit because imports are greater than exports.

The first two possibilities we might call A and B:

A: A nation can run an external deficit and equal government surplus while the private domestic sector is saving overall.

B: A nation can run an external deficit and equal government surplus while the private domestic sector is dis-saving overall.

So Option A says the private domestic sector is saving overall, whereas Option B say the private domestic sector is dis-saving (and going into increasing indebtedness). These options are captured in the first column of the Table. So the arithmetic example depicts an external sector deficit of 2 per cent of GDP and an offsetting budget surplus of 2 per cent of GDP.

You can see that the private sector balance is positive (that is, the sector is spending more than they are earning – Investment is greater than Saving – and has to be equal to 4 per cent of GDP.

Given that the only proposition that can be true is:

B: A nation can run an external deficit and equal government surplus while the private domestic sector is dis-saving overall.

Column 2 in the Table captures Option C:

C: A nation can run an external deficit and a larger government surplus while the private domestic sector is saving overall.

So the current account deficit is equal to 2 per cent of GDP while the surplus is now larger at 3 per cent of GDP. You can see that the private domestic deficit rises to 5 per cent of GDP to satisfy the accounting rule that the balances sum to zero.

The final option available is:

D: None of the above are possible as they all defy the sectoral balances accounting identity.

It cannot be true because as the Table data shows the rule that the sectoral balances add to zero because they are an accounting identity is satisfied in both cases.

So if the G is spending less than it is “earning” and the external sector is adding less income (X) than it is absorbing spending (M), then the other spending components must be greater than total income

The following blogs may be of further interest to you:

• Barnaby, better to walk before we run
• Stock-flow consistent macro models
• Norway and sectoral balances
• The OECD is at it again!