If economy-wide average nominal wages fail to keep pace with the inflation rate then it means the profit share in GDP is rising.
Answer: False
The answer is False.
The wage share in nominal GDP is expressed as the total wage bill as a percentage of nominal GDP. Economists differentiate between nominal GDP ($GDP), which is total output produced at market prices and real GDP (GDP), which is the actual physical equivalent of the nominal GDP. We will come back to that distinction soon.
To compute the wage share we need to consider total labour costs in production and the flow of production ($GDP) each period.
Employment (L) is a stock and is measured in persons (averaged over some period like a month or a quarter or a year.
The wage bill is a flow and is the product of total employment (L) and the average nominal wage (w) prevailing at any point in time. Stocks (L) become flows if it is multiplied by a flow variable (W). So the wage bill is the total labour costs in production per period.
So the wage bill = W.L
The wage share is just the total labour costs expressed as a proportion of $GDP - (W.L)/$GDP in nominal terms, usually expressed as a percentage. We can actually break this down further.
Labour productivity (LP) is the units of real GDP per person employed per period. Using the symbols already defined this can be written as:
LP = GDP/L
so it tells us what real output (GDP) each labour unit that is added to production produces on average.
We can also define another term that is regularly used in the media - the real wage - which is the purchasing power equivalent on the nominal wage that workers get paid each period. To compute the real wage we need to consider two variables: (a) the nominal wage (W) and the aggregate price level (P).
We might consider the aggregate price level to be measured by the consumer price index (CPI) although there are huge debates about that. But in a sense, this macroeconomic price level doesn't exist but represents some abstract measure of the general movement in all prices in the economy.
Macroeconomics is hard to learn because it involves these abstract variables that are never observed - like the price level, like "the interest rate" etc. They are just stylisations of the general tendency of all the different prices and interest rates.
Now the nominal wage (W) - that is paid by employers to workers is determined in the labour market - by the contract of employment between the worker and the employer. The price level (P) is determined in the goods market - by the interaction of total supply of output and aggregate demand for that output although there are complex models of firm price setting that use cost-plus mark-up formulas with demand just determining volume sold. We shouldn't get into those debates here.
The inflation rate is just the continuous growth in the price level (P). A once-off adjustment in the price level is not considered by economists to constitute inflation.
So the real wage (w) tells us what volume of real goods and services the nominal wage (W) will be able to command and is obviously influenced by the level of W and the price level. For a given W, the lower is P the greater the purchasing power of the nominal wage and so the higher is the real wage (w).
We write the real wage (w) as W/P. So if W = 10 and P = 1, then the real wage (w) = 10 meaning that the current wage will buy 10 units of real output. If P rose to 2 then w = 5, meaning the real wage was now cut by one-half.
Nominal GDP ($GDP) can be written as P.GDP, where the P values the real physical output.
Now if you put of these concepts together you get an interesting framework. To help you follow the logic here are the terms developed and be careful not to confuse $GDP (nominal) with GDP (real):
By substituting the expression for Nominal GDP into the wage share measure we get:
Wage share = (W.L)/P.GDP
In this area of economics, we often look for alternative way to write this expression - it maintains the equivalence (that is, obeys all the rules of algebra) but presents the expression (in this case the wage share) in a different "view".
So we can write as an equivalent:
Wage share = (W/P).(L/GDP)
Now if you note that (L/GDP) is the inverse (reciprocal) of the labour productivity term (GDP/L). We can use another rule of algebra (reversing the invert and multiply rule) to rewrite this expression again in a more interpretable fashion.
So an equivalent but more convenient measure of the wage share is:
Wage share = (W/P)/(GDP/L) - that is, the real wage (W/P) divided by labour productivity (GDP/L).
I won't show this but I could also express this in growth terms such that if the growth in the real wage equals labour productivity growth the wage share is constant. The algebra is simple but we have done enough of that already.
That journey might have seemed difficult to non-economists (or those not well-versed in algebra) but it produces a very easy to understand formula for the wage share.
Two other points to note. The wage share is also equivalent to the real unit labour cost (RULC) measures that Treasuries and central banks use to describe trends in costs within the economy. Please read my blog - Saturday Quiz - May 15, 2010 - answers and discussion - for more discussion on this point.
Now it becomes obvious that if the nominal wage (W) and the price level (P) are growing at the pace the real wage is constant. And if the real wage is growing at the same rate as labour productivity, then both terms in the wage share ratio are equal and so the wage share is constant.
However, if the real wage is falling we cannot conclude that the wage share is also falling. Given the nature of ratios, if the numerator (in this case, the real wage) is falling but not by as much as the denominator (in this case, labour productivity) then the overall ratio can actually be rising.
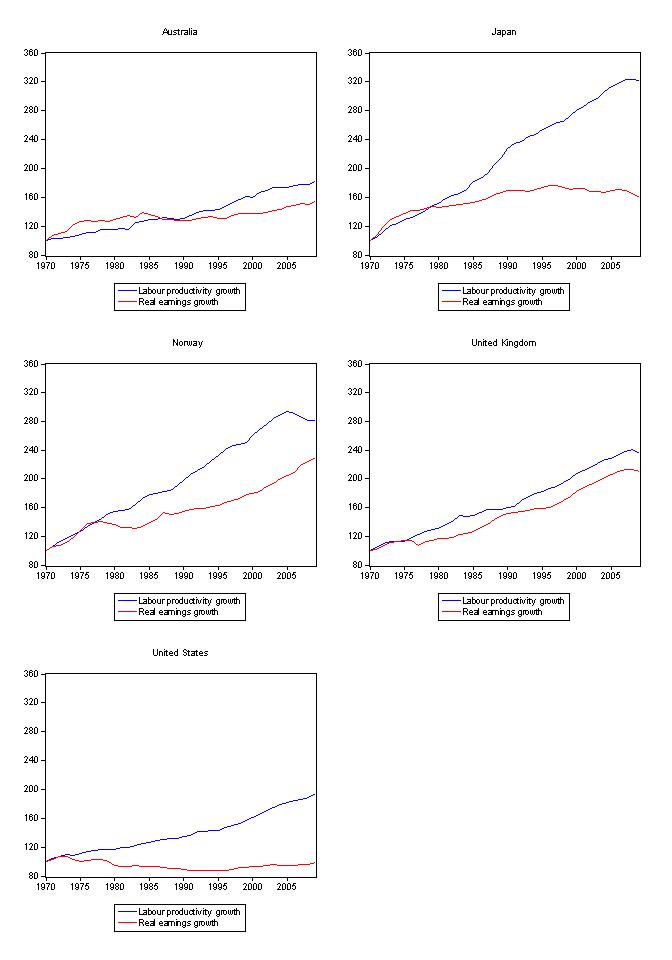
I provided this graphic in the blog - When will the workers wake up? 0 and it shows index numbers (1970=100) for Real Earnings and Labour Productivity to give you some idea of how each has grown over the last 40 years. I chose Australia, Japan, Norway, the UK and the USA for comparison being a broad selection of different types of economies.
While the relationship between real earnings growth and labour productivity growth over this period is interesting in itself for each individual country, I also set equivalent vertical axis scale so you can also compare between countries.
You can see that in the nations shown real wages growth has lagged behind labour productivity growth (to varying degrees). You also see that workers in Norway have enjoyed much better outcomes than workers elsewhere. The US stands out clearly as the worst performed nation.
In most cases the real wage is actually rising but the wage share is falling (profit share rising) because productivity growth is rising faster.
The following blogs may be of further interest to you: