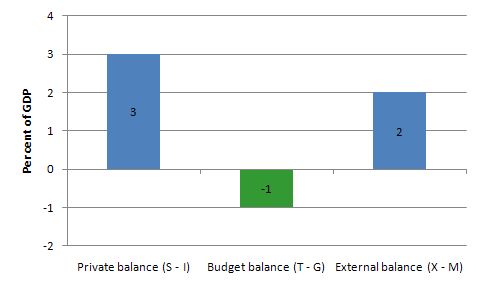
If net exports are running at 2 per cent of GDP, and the private domestic sector overall is saving an equivalent of 3 per cent of GDP, the government must be running
Answer: A deficit equal to 1 per cent of GDP.
The answer is Option C Be running a deficit equal to 1 per cent of GDP.
This question tests your knowledge of the sectoral balances that are derived from the National Accounts.
First, you need to understand the basic relationship between the sectoral flows and the balances that are derived from them. The flows are derived from the National Accounting relationship between aggregate spending and income. So:
(1) Y = C + I + G + (X - M)
where Y is GDP (income), C is consumption spending, I is investment spending, G is government spending, X is exports and M is imports (so X - M = net exports).
Another perspective on the national income accounting is to note that households can use total income (Y) for the following uses:
(2) Y = C + S + T
where S is total saving and T is total taxation (the other variables are as previously defined).
You than then bring the two perspectives together (because they are both just "views" of Y) to write:
(3) C + S + T = Y = C + I + G + (X - M)
You can then drop the C (common on both sides) and you get:
(4) S + T = I + G + (X - M)
Then you can convert this into the familiar sectoral balances accounting relations which allow us to understand the influence of fiscal policy over private sector indebtedness.
So we can re-arrange Equation (4) to get the accounting identity for the three sectoral balances - private domestic, government fiscal balance and external:
(S - I) = (G - T) + (X - M)
The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.
Another way of saying this is that total private savings (S) is equal to private investment (I) plus the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)), where net exports represent the net savings of non-residents.
All these relationships (equations) hold as a matter of accounting and not matters of opinion.
Thus, when an external deficit (X - M < 0) and public surplus (G - T < 0) coincide, there must be a private deficit. While private spending can persist for a time under these conditions using the net savings of the external sector, the private sector becomes increasingly indebted in the process.
Second, you then have to appreciate the relative sizes of these balances to answer the question correctly.
The rule is that the sectoral balances have to sum to zero. So if we write the condition above as:
(S - 1) - (G - T) - (X - M) = 0
And substitute the values of the question we get:
3 - (G - T) - 2 = 0
We can solve this for (G - T) as
(G - T) = 3 - 2 = 1
Given the construction (G - T) a positive number (1) is a deficit.
The outcome is depicted in the following graph.
This tells us that even if the external sector is growing strongly and is in surplus there may still be a need for public deficits. This will occur if the private domestic sector seek to save at a proportion of GDP higher than the external surplus.
The economics of this situation might be something like this. The external surplus would be adding to overall aggregate demand (the injection from exports exceeds the drain from imports). However, if the drain from private sector spending (S > I) is greater than the external injection then the only way output and income can remain constant is if the government is in deficit.
National income adjustments would occur if the private domestic sector tried to push for higher saving overall - income would fall (because overall spending fell) and the government would be pushed into deficit whether it liked it or not via falling revenue and rising welfare payments.
You may wish to read the following blogs for more information: