Take an economy that is running a current account deficit equivalent to 2 per cent of its GDP with a government recording a budget surplus of 2 per cent of GDP. If the budget balance stays constant and the external surplus rises to the equivalent of 4 per cent of GDP then you can conclude that national income also rises and the private domestic sector switches from a position where it is spending more than it is earning (deficit equivalent to 2 per cent of GDP) to a position where it is saving overall by 2 per cent of GDP.
Answer: False
The answer is False.
This question requires an understanding of the sectoral balances that can be derived from the National Accounts. But it also requires some understanding of the behavioural relationships within and between these sectors which generate the outcomes that are captured in the National Accounts and summarised by the sectoral balances.
We know that from an accounting sense, if the external sector overall is in deficit, then it is impossible for both the private domestic sector and government sector to run surpluses. One of those two has to also be in deficit to satisfy the accounting rules.
The important point is to understand what behaviour and economic adjustments drive these outcomes.
So here is the accounting (again). The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X - M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X - M).
From the uses perspective, national income (GDP) can be used for:
GDP = C + S + T
which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.
Equating these two perspectives we get:
C + S + T = GDP = C + I + G + (X - M)
So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.
(I - S) + (G - T) + (X - M) = 0
That is the three balances have to sum to zero. The sectoral balances derived are:
These balances are usually expressed as a per cent of GDP but that doesn't alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.
A simplification is to add (I - S) + (X - M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).
This is also a basic rule derived from the national accounts and has to apply at all times.
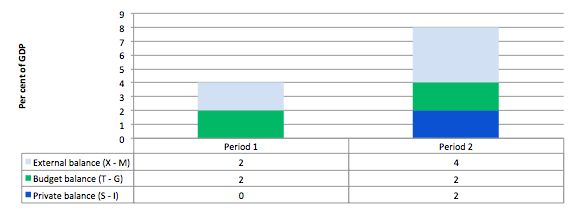
Consider the following graph and accompanying table which depicts two periods outlined in the question.
In Period 1, with an external surplus of 2 per cent of GDP and a budget surplus of 2 per cent of GDP the private domestic balance is zero. The demand injection from the external sector is exactly offset by the demand drain (the fiscal drag) coming from the budget balance and so the private sector can neither net save overall nor spend more than its earns. So the starting position for the private domestic sector is a balanced state.
In Period 2, with the external sector adding more to demand now - surplus equal to 4 per cent of GDP and the budget balance unchanged (this is stylised - in the real world the budget will certainly change), there is a stimulus to spending and national income would rise.
The rising national income also provides the capacity for the private sector to save overall and so they can now save 2 per cent of GDP. Please note the difference between saving and saving overall.
The fiscal drag is overwhelmed by the rising net exports.
This is a highly stylised example and you could tell a myriad of stories that would be different in description but none that could alter the basic point.
If the drain on spending (from the public sector) is more than offset by an external demand injection, then GDP rises and the private sector overall saving increases.
If the drain on spending from the budget outweighs the external injections into the spending stream then GDP falls (or growth is reduced) and the overall private balance would fall into deficit.
You may wish to read the following blogs for more information: