Only one of the following propositions is possible (with all balances expressed as a per cent of GDP)
Answer: A nation can run a current account deficit accompanied by a government sector surplus of equal proportion to GDP, while the private domestic sector is spending more than they are earning.
The best answer is the second option - "A nation can run a current account deficit accompanied by a government sector surplus of equal proportion to GDP, while the private domestic sector is spending more than they are earning".
This is a question about the sectoral balances - the government budget balance, the external balance and the private domestic balance - that have to always add to zero because they are derived as an accounting identity from the national accounts.
To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X - M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X - M).
From the uses perspective, national income (GDP) can be used for:
GDP = C + S + T
which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.
Equating these two perspectives we get:
C + S + T = GDP = C + I + G + (X - M)
So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.
(I - S) + (G - T) + (X - M) = 0
That is the three balances have to sum to zero. The sectoral balances derived are:
These balances are usually expressed as a per cent of GDP but that doesn't alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.
A simplification is to add (I - S) + (X - M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).
This is also a basic rule derived from the national accounts and has to apply at all times.
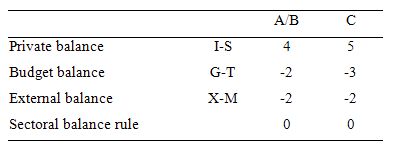
The following Table represents the three options in percent of GDP terms. To aid interpretation remember that (I-S) > 0 means that the private domestic sector is spending more than they are earning; that (G-T) < 0 means that the government is running a surplus because T > G; and (X-M) < 0 means the external position is in deficit because imports are greater than exports.
The first two possibilities we might call A and B:
A: A nation can run a current account deficit with an offsetting government sector surplus, while the private domestic sector is spending less than they are earn
B: A nation can run a current account deficit with an offsetting government sector surplus, while the private domestic sector is spending more than they are earning.
So Option A says the private domestic sector is saving overall, whereas Option B say the private domestic sector is dis-saving (and going into increasing indebtedness). These options are captured in the first column of the Table. So the arithmetic example depicts an external sector deficit of 2 per cent of GDP and an offsetting budget surplus of 2 per cent of GDP.
You can see that the private sector balance is positive (that is, the sector is spending more than they are earning - Investment is greater than Saving - and has to be equal to 4 per cent of GDP.
Given that the only proposition that can be true is:
B: A nation can run a current account deficit with an offsetting government sector surplus, while the private domestic sector is spending more than they are earning.
Column 2 in the Table captures Option C:
C: A nation can run a current account deficit with a government sector surplus that is larger, while the private domestic sector is spending less than they are earning.
So the current account deficit is equal to 2 per cent of GDP while the surplus is now larger at 3 per cent of GDP. You can see that the private domestic deficit rises to 5 per cent of GDP to satisfy the accounting rule that the balances sum to zero.
The final option available is:
D: None of the above are possible as they all defy the sectoral balances accounting identity.
It cannot be true because as the Table data shows the rule that the sectoral balances add to zero because they are an accounting identity is satisfied in both cases.
So what is the economic rationale for this result?
If the nation is running an external deficit it means that the contribution to aggregate demand from the external sector is negative - that is net drain of spending - dragging output down.
The external deficit also means that foreigners are increasing financial claims denominated in the local currency. Given that exports represent a real costs and imports a real benefit, the motivation for a nation running a net exports surplus (the exporting nation in this case) must be to accumulate financial claims (assets) denominated in the currency of the nation running the external deficit.
A fiscal surplus also means the government is spending less than it is "earning" and that puts a drag on aggregate demand and constrains the ability of the economy to grow.
In these circumstances, for income to be stable, the private domestic sector has to spend more than they earn.
You can see this by going back to the aggregate demand relations above. For those who like simple algebra we can manipulate the aggregate demand model to see this more clearly.
Y = GDP = C + I + G + (X - M)
which says that the total national income (Y or GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X - M).
So if the G is spending less than it is "earning" and the external sector is adding less income (X) than it is absorbing spending (M), then the other spending components must be greater than total income
The following blogs may be of further interest to you:
Premium