Assume that the national accounts of a nation is reveal that its external surplus is equivalent to 2 per cent of GDP and the private domestic sector is saving overall 3 per cent of GDP. We would also observe
Answer: A budget deficit equal to 1 per cent of GDP.
The answer is Option (a) - A budget deficit equal to 1 per cent of GDP.
This question requires an understanding of the sectoral balances that can be derived from the National Accounts. But it also requires some understanding of the behavioural relationships within and between these sectors which generate the outcomes that are captured in the National Accounts and summarised by the sectoral balances.
Refreshing the balances (again) - we know that from an accounting sense, if the external sector overall is in deficit, then it is impossible for both the private domestic sector and government sector to run surpluses. One of those two has to also be in deficit to satisfy the accounting rules.
The important point is to understand what behaviour and economic adjustments drive these outcomes.
So here is the accounting (again). The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X - M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X - M).
From the uses perspective, national income (GDP) can be used for:
GDP = C + S + T
which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.
Equating these two perspectives we get:
C + S + T = GDP = C + I + G + (X - M)
So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.
(I - S) + (G - T) + (X - M) = 0
That is the three balances have to sum to zero. The sectoral balances derived are:
These balances are usually expressed as a per cent of GDP but that doesn't alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.
A simplification is to add (I - S) + (X - M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).
This is also a basic rule derived from the national accounts and has to apply at all times.
So what economic behaviour might lead to the outcome specified in the question?
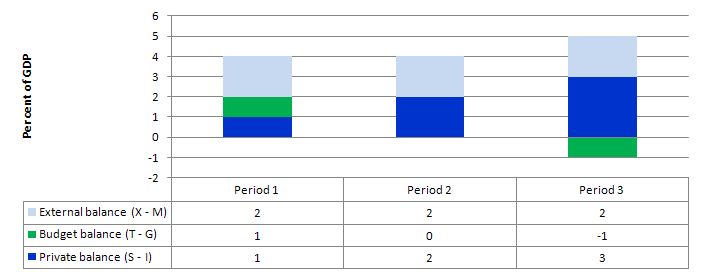
The following graph shows three situations where the external sector is in surplus of 2 per cent of GDP and the private domestic balance is in surplus of varying proportions of GDP (note I have written the budget balance as (T - G).
In Period 1, the private domestic balance is in surplus (1 per cent of GDP), which means it is saving overall (spending less than the total private income) and the budget is also in surplus (1 per cent of GDP). The net injection to demand from the external sector (equivalent to 2 per cent of GDP) is sufficient to "fund" the overall private sector saving drain from expenditure without compromising economic growth. The growth in income would also allow the budget to be in surplus (via tax revenue).
In Period 2, the rise in overall private domestic saving drains extra aggregate demand and necessitates a more expansionary position from the government (relative to Period 1), which in this case manifests as a balanced public budget,'
Period 3, relates to the data presented in the question - an external surplus of 2 per cent of GDP and private domestic saving equal to 3 per cent of GDP. Now the demand injection from the external sector is being more than offset by the demand drain from private domestic saving. The income adjustments that would occur in this economy would then push the budget into deficit of 1 per cent of GDP.
The movements in income associated with the spending and revenue patterns will ensure these balances arise.
The general rule is that the government budget deficit (surplus) will always equal the non-government surplus (deficit).
So if there is an external surplus that is less than the overall private domestic sector saving (a surplus) then there will always be a budget deficit. The higher the overall private saving is relative to the external surplus, the larger the deficit.
The following blogs may be of further interest to you: