The private domestic sector can save overall even if the government budget balance is in surplus as long as net exports are positive.
Answer: False
The answer is False.
This is a question about the relative magnitude of the sectoral balances - the government budget balance, the external balance and the private domestic balance. The balances taken together always add to zero because they are derived as an accounting identity from the national accounts. The balances reflect the underlying economic behaviour in each sector which is interdependent - given this is a macroeconomic system we are considering.
To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
GDP = C + I + G + (X - M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X - M).
From the uses perspective, national income (GDP) can be used for:
GDP = C + S + T
which says that GDP (income) ultimately comes back to households who consume (C), save (S) or pay taxes (T) with it once all the distributions are made.
Equating these two perspectives we get:
C + S + T = GDP = C + I + G + (X - M)
So after simplification (but obeying the equation) we get the sectoral balances view of the national accounts.
(I - S) + (G - T) + (X - M) = 0
That is the three balances have to sum to zero. The sectoral balances derived are:
These balances are usually expressed as a per cent of GDP but that doesn't alter the accounting rules that they sum to zero, it just means the balance to GDP ratios sum to zero.
A simplification is to add (I - S) + (X - M) and call it the non-government sector. Then you get the basic result that the government balance equals exactly $-for-$ (absolutely or as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances).
This is also a basic rule derived from the national accounts and has to apply at all times.
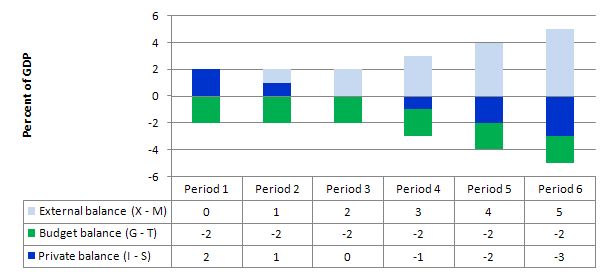
The following graph with accompanying data table lets you see the evolution of the balances expressed in terms of percent of GDP. In each period I just held the budget balance at a constant surplus (2 per cent of GDP) (green bars). This is is artificial because as economic activity changes the automatic stabilisers would lead to endogenous changes in the budget balance. But we will just assume there is no change for simplicity. It doesn't violate the logic.
To aid interpretation remember that (I-S) > 0 means that the private domestic sector is spending more than they are earning; that (G-T) < 0 means that the government is running a surplus because T > G; and (X-M) < 0 means the external position is in deficit because imports are greater than exports.
If the nation is running an external surplus it means that the contribution to aggregate demand from the external sector is positive - that is net addition to spending which would increase output and national income.
The external deficit also means that foreigners are decreasing financial claims denominated in the local currency. Given that exports represent a real cost and imports a real benefit, the motivation for a nation running a net exports surplus (the exporting nation in this case) must be to accumulate financial claims (assets) denominated in the currency of the nation running the external deficit.
A fiscal surplus also means the government is spending less than it is "earning" and that puts a drag on aggregate demand and constrains the ability of the economy to grow. So the question is what are the relative magnitudes of the external add and the budget subtract from income?
In Period 1, there is an external balance (X - M = 0) and then for each subsequent period the external balance goes into surplus incrementing by 1 per cent of GDP each period (light-blue bars).
You can see that in the first two periods, private domestic saving is negative, then as the demand injection from the external surplus offsets the fiscal drag arising from the budget surplus, the private domestic sector breakeven (spending as much as they earn, so I - S = 0). Then the demand add overall arising from the net positions of the external and public sectors is positive and the income growth would allow the private sector to save. That is increasingly so as the net demand add increases with the increasing external surplus.
The following blogs may be of further interest to you: