Nations with external deficits operate within the constraint that national income movements will ensure that the two remaining sectors (government and private domestic) will spend more than they receive, irrespective of the GDP growth rate.
Answer: False
The answer is False.
The sectoral balances framework tells us that when the external sector is in deficit, then it is impossible for both the private domestic sector and government sector to run surpluses. At least one of those two has to also be in deficit to satisfy the accounting rules.
National income movements will always deliver that outcome and the balances that each sector records will be determined by a combination of their own spending decisions and the spillovers from the other sectors that impact on their respective incomes.
It also follows that it doesn't matter how fast GDP is growing.
To refresh your memory the balances are derived as follows. The basic income-expenditure model in macroeconomics can be viewed in (at least) two ways: (a) from the perspective of the sources of spending; and (b) from the perspective of the uses of the income produced. Bringing these two perspectives (of the same thing) together generates the sectoral balances.
From the sources perspective we write:
(1) GDP = C + I + G + (X - M)
which says that total national income (GDP) is the sum of total final consumption spending (C), total private investment (I), total government spending (G) and net exports (X - M).
Expression (1) tells us that total income in the economy per period will be exactly equal to total spending from all sources of expenditure.
We also have to acknowledge that financial balances of the sectors are impacted by net government taxes (T) which includes all tax revenue minus total transfer and interest payments (the latter are not counted independently in the expenditure Expression (1)).
Further, as noted above the trade account is only one aspect of the financial flows between the domestic economy and the external sector. we have to include net external income flows (FNI).
Adding in the net external income flows (FNI) to Expression (2) for GDP we get the familiar gross national product or gross national income measure (GNP):
(2) GNP = C + I + G + (X - M) + FNI
To render this approach into the sectoral balances form, we subtract total net taxes (T) from both sides of Expression (3) to get:
(3) GNP - T = C + I + G + (X - M) + FNI - T
Now we can collect the terms by arranging them according to the three sectoral balances:
(4) (GNP - C - T) - I = (G - T) + (X - M + FNI)
The the terms in Expression (4) are relatively easy to understand now.
The term (GNP - C - T) represents total income less the amount consumed less the amount paid to government in taxes (taking into account transfers coming the other way). In other words, it represents private domestic saving.
The left-hand side of Equation (4), (GNP - C - T) - I, thus is the overall saving of the private domestic sector, which is distinct from total household saving denoted by the term (GNP - C - T).
In other words, the left-hand side of Equation (4) is the private domestic financial balance and if it is positive then the sector is spending less than its total income and if it is negative the sector is spending more than it total income.
The term (G - T) is the government financial balance and is in deficit if government spending (G) is greater than government tax revenue minus transfers (T), and in surplus if the balance is negative.
Finally, the other right-hand side term (X - M + FNI) is the external financial balance, commonly known as the current account balance (CAD). It is in surplus if positive and deficit if negative.
In English we could say that:
The private financial balance equals the sum of the government financial balance plus the current account balance.
We can re-write Expression (6) in this way to get the sectoral balances equation:
(5) (S - I) = (G - T) + CAD
which is interpreted as meaning that government sector deficits (G - T > 0) and current account surpluses (CAD > 0) generate national income and net financial assets for the private domestic sector.
Conversely, government surpluses (G - T < 0) and current account deficits (CAD < 0) reduce national income and undermine the capacity of the private domestic sector to add financial assets.
Expression (5) can also be written as:
(6) [(S - I) - CAD] = (G - T)
where the term on the left-hand side [(S - I) - CAD] is the non-government sector financial balance and is of equal and opposite sign to the government financial balance.
This is the familiar MMT statement that a government sector deficit (surplus) is equal dollar-for-dollar to the non-government sector surplus (deficit).
The sectoral balances equation says that total private savings (S) minus private investment (I) has to equal the public deficit (spending, G minus taxes, T) plus net exports (exports (X) minus imports (M)) plus net income transfers.
All these relationships (equations) hold as a matter of accounting and not matters of opinion.
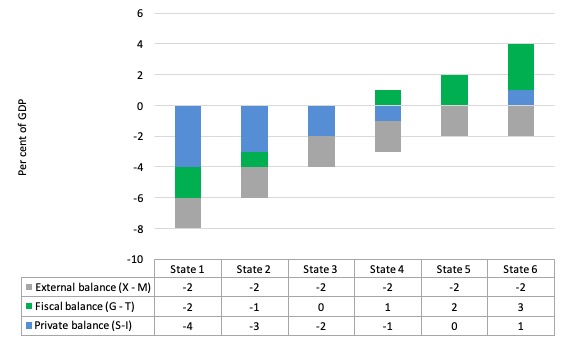
Consider the following graph and associated table of data which shows six states. All states have a constant external deficit equal to 2 per cent of GDP (gray columns).
A government deficit is a positive number (G > T), a private domestic deficit is a negative number (S < I).
State 1 show a government running a surplus equal to 2 per cent of GDP (green columns). As a consequence, the private domestic balance is in deficit of 4 per cent of GDP (blue columns).
State 2 shows that when the fiscal surplus falls to 1 per cent of GDP, the private domestic deficit is reduced.
State 3 is a fiscal balance (G = T) and then the private domestic deficit is exactly equal to the external deficit. So the private sector spending more than they earn exactly funds the desire of the external sector to accumulate financial assets in the currency of issue in this country.
States 4 to 6 shows what happens when the fiscal balance goes into deficit - the private domestic sector (given the external deficit) can then start reducing its deficit and by State 5 it is in balance.
Then by State 6 the private domestic sector is able to net save overall (that is, spend less than its income) because the fiscal deficit (adding demand) is greater than the external deficit (draining demand).
Note also that the government balance equals exactly $-for-$ (as a per cent of GDP) the non-government balance (the sum of the private domestic and external balances). This is also a basic rule derived from the national accounts.
Most countries currently run external deficits. The crisis was marked by households reducing consumption spending growth to try to manage their debt exposure and private investment retreating. The consequence was a major spending gap which pushed fiscal balances into deficit via the automatic stabilisers.
The only way to get income growth going in this context and to allow the private sector surpluses to build was to increase the deficits beyond the impact of the automatic stabilisers. The reality is that this policy change hasn't delivered large enough fiscal deficits (even with external deficits narrowing). The result has been large negative income adjustments which brought the sectoral balances into equality at significantly lower levels of economic activity.
The following blogs may be of further interest to you: